Radiative heat transfer in semitransparent media is described by the radiative transfer equation (RTE). Solving this equation is challenging in terms of computational costs. However, depending on a medium’s radiation properties, simplifications exist that allow the solving of such models in a fraction of the time. This blog post gives an overview of the available methods and when they can be applied.
Defining the Radiative Transfer Equation
An incident beam that travels in direction \Omega through a participating medium interacts with the medium. Part of its intensity, I(\Omega), is absorbed by the fraction \kappa I(\Omega), where \kappa (m^{-1}) is the absorption coefficient. Another fraction is scattered in another direction, \sigma_s I(\Omega), where \sigma_s(m^{-1}) is the scattering coefficient. The intensity in a given direction is attenuated by scattering in a different direction and augmented by radiation coming from a different direction. This is described by:
(1)
where \phi(\Omega^{\prime},\Omega) is the scattering phase function that describes the probability of a ray from direction \Omega^{\prime} being scattered into direction \Omega. The medium itself can emit radiation in all directions by the factor \kappa I_b, where I_b is the intensity of a blackbody.
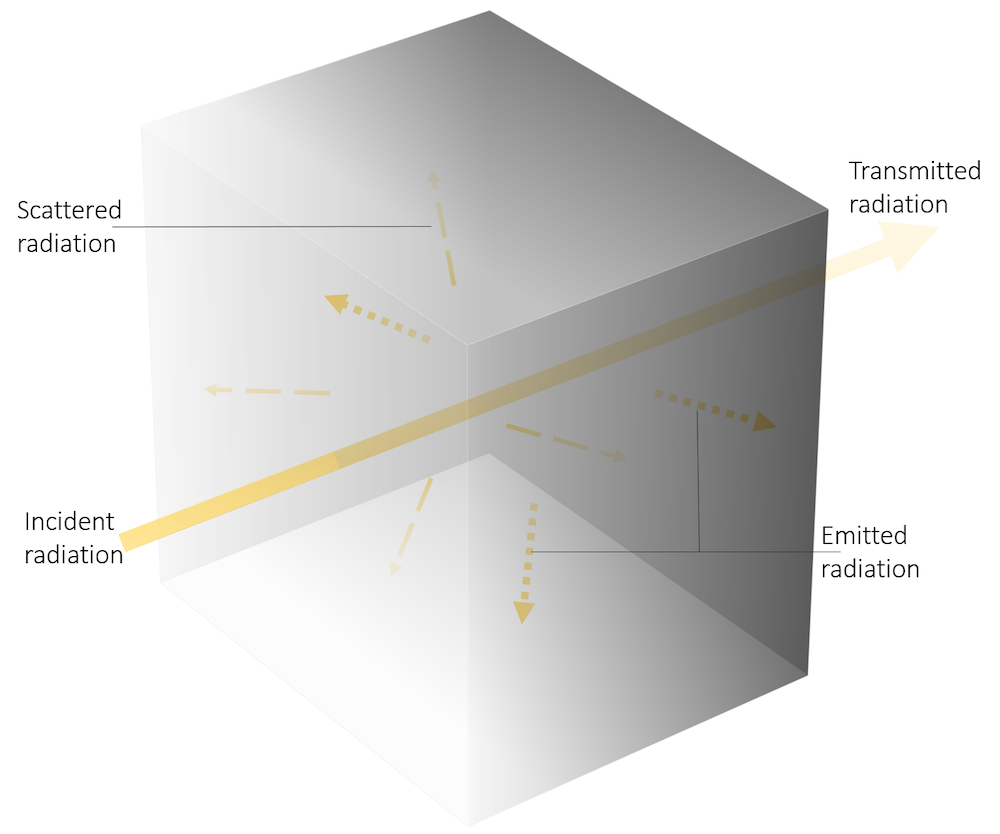
Radiation interacting with a semitransparent medium.
All of these effects are fully described by an integro-differential equation called RTE:
(2)
The key to solving this equation lies in the approximation of the scattering integral. In combination with heat transfer, the incident radiation
(3)
and the radiative heat flux
(4)
are important quantities.
Before we discuss the different methods to solve this equation, we introduce another quantity that describes the participating medium — the optical thickness or optical depth:
(5)
It describes how transparent the medium is to radiation. If \tau\ll 1, the medium is called “optically thin”, and if \tau\gg1, “optically thick”.
Methods for Solving the RTE
The following sections give an overview of the four methods available with the COMSOL Multiphysics® software to solve the RTE:
- Discrete ordinates method (DOM)
- P1 approximation
- Rosseland approximation
- Beer–Lambert law
Except for the last one, we owe all of these methods to astrophysics and its analysis of stellar atmospheres. A comprehensive book about this complex topic is Radiative Heat Transfer by M.F. Modest (Ref. 1). It contains detailed explanations and derivations of the solution methods that go beyond the scope of this blog post.
Method 1: The Discrete Ordinates Method
The most general method of solving the RTE is the DOM. Its name indicates the idea behind this method. The integral over the angular space is divided into discrete directions. Thus, one partial differential equation (PDE) per discrete ordinate remains to be solved for the intensity, I:
(6)
where \mathbf{S}_i is the ith discrete ordinate and w_j, the quadrature weights.
The details of how to divide the angular space into discrete ordinates are described in this previous blog post. The default SN method uses a symmetric quadrature set of order N and divides the 3D angular space in N(N+2) directions. The figure below illustrates the discrete ordinates for the symmetric even quadrature set and different order, N.
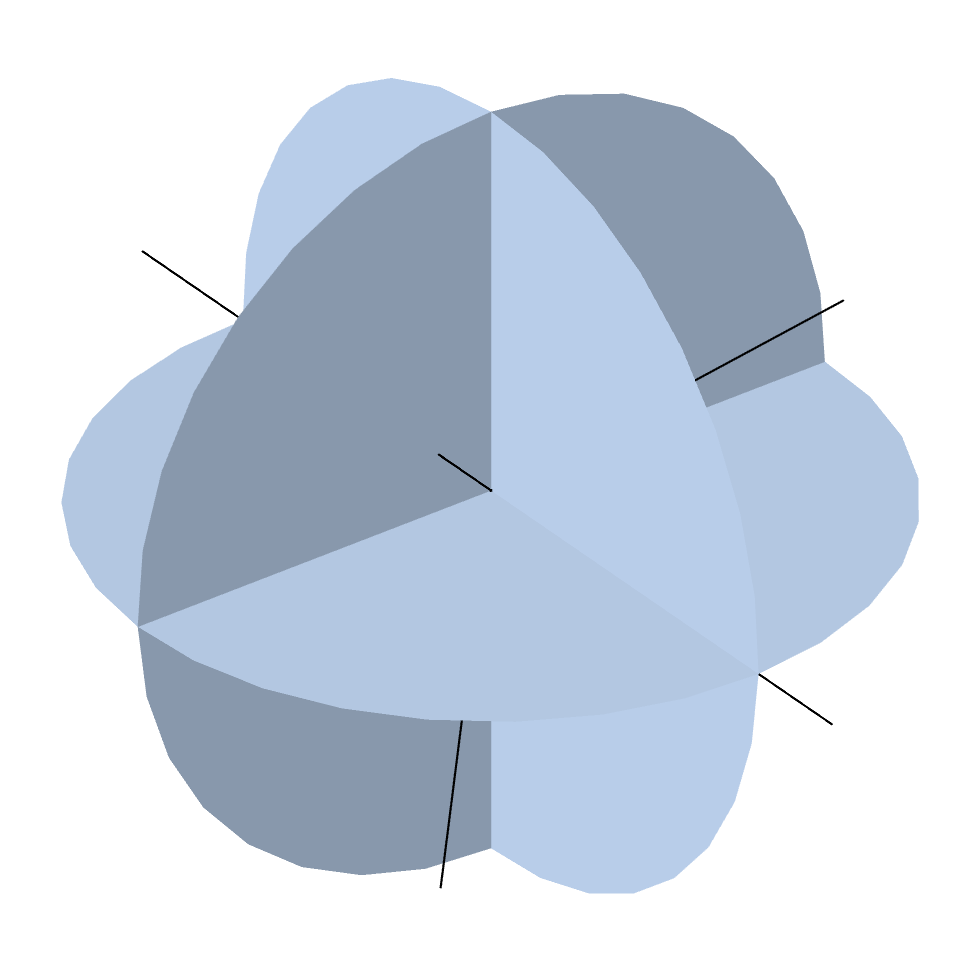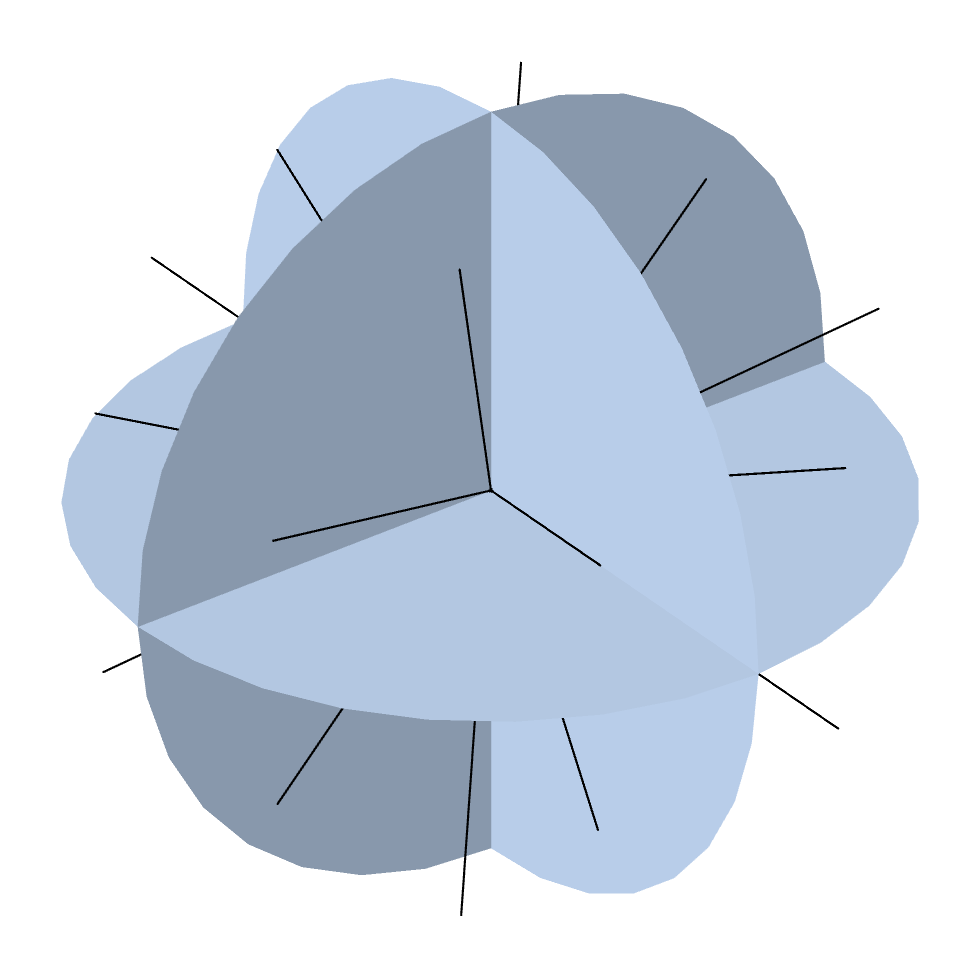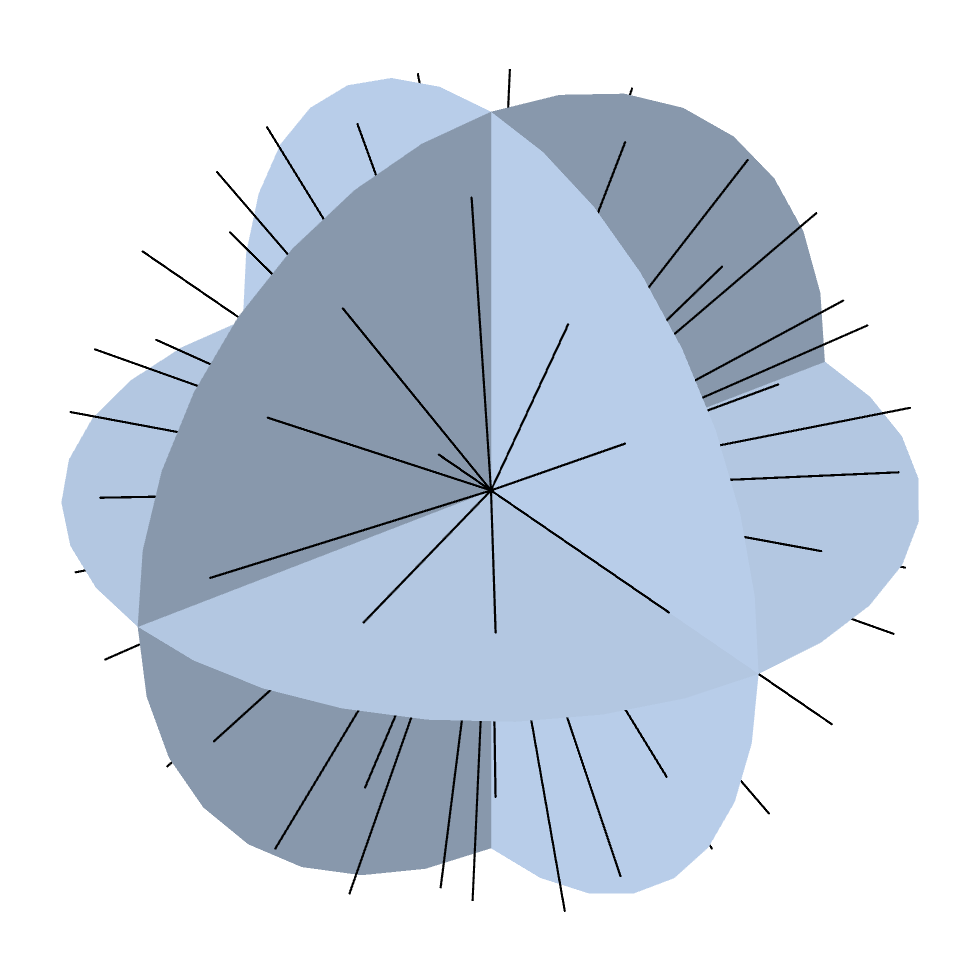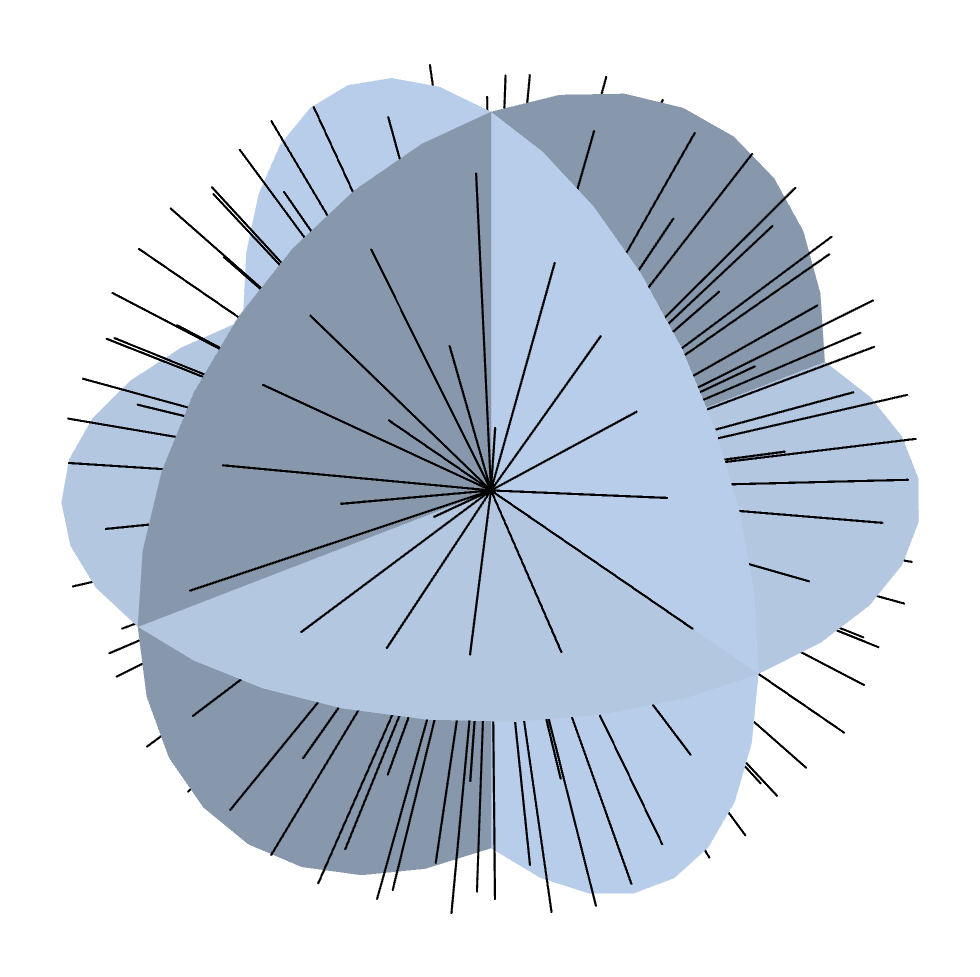
Discrete ordinates for the level symmetric even quadrature set from S2 up to S12 (8–168 directions).
The default S4 method is sufficient for many applications but already introduces 24 dependent variables for the intensities. The major advantage of the DOM over the other methods is the high accuracy in arbitrary configurations because of its discretization of the angular space. Additionally, the method can handle various forms of the scattering phase functions: isotropic, linear or polynomial anisotropic, and Henyey–Greenstein.
Because this method is computationally expensive and the required memory easily exceeds the available memory on common workstations for complex 3D geometries, we want to talk briefly about a simple way to tweak the solver — the performance index, which is available at the interface level.
Let’s say we need to be very accurate and use the S8 method, which adds 80 additional equations to the model. The solver splits these variables into segregated groups, and each group is computed in a single iterative step before the solver moves on to the next group. The performance index controls the number of groups that are created. For a performance index of 0 (minimum value), 10 groups are created, where each group contains 8 intensity variables. If the performance index is set to 1 (maximum value), each intensity variable goes into a separate, segregated group and the required memory remains low. This approach also works for larger models, but the computational time increases.
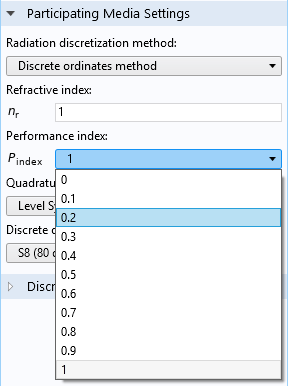
Performance index to control the solver.
Method 2: The P1 Approximation
Instead of using discrete ordinates, the P1 method is based on spherical harmonics to discretize the angular space. They are eigenfunctions of the Laplace operator in spherical coordinates. The P1 approximation uses linear terms only and from this, it emerges that solving the following equation for Eq. (3) is equivalent to:
(7)
D_\textrm{P1} is the P1 diffusion coefficient, defined as:
(8)
with the linear Legendre coefficient, a_1, for the scattering phase function.
Hence, with the P1 method, isotropic and linear anisotropic scattering can be considered. The second term on the left-hand side corresponds to the radiative heat source, Q_\textrm{r}. Thus, only one additional equation is needed to take radiation transport into account.
Method 3: The Rosseland Approximation
First, let’s recall the stationary heat equation for a medium with density \rho(kg/m^3), heat capacity C_p(J/(kg\cdot K)), and thermal conductivity k(W/(m\cdot K):
(9)
The first term on the left-hand side is the convective term, and on the right side is the heat source term.
Let’s take a closer look at the conductive term where the heat flux, \mathbf{q}, follows Fourier’s law of heat conduction:
(10)
Getting back to radiation in participating media, light propagation behaves similarly to heat conduction under the assumption of large optical depths (\tau\gg 1), and we can rewrite Eq. (10) as follows:
(11)
with the highly nonlinear “radiative conductivity”, k_\textrm{R}:
(12)
with \beta_\textrm{R}=\kappa+\sigma_\textrm{s} being the Rosseland mean extinction coefficient and \sigma(W/(m^2K^4)), the Stefan–Boltzmann constant.
From a computational point of view, no additional equation is required to account for radiation in participating media. Just a highly nonlinear conductivity term appears. However, the number of problems for which this approximation is valid is limited: mainly, radiation that depends on the temperature and its gradient only and not on its direction or distance to the source, which is valid at very large optical depths. This applies to stellar atmospheres, for which the method was first developed by Rosseland. It is also a common method in the glass industry for a wide range of uses.
Because the Rosseland approximation inserts an additional term to Eq. (9), it is available as an extension of the Solid feature and is called Optically Thick Participating Medium.

Subfeature to consider radiation at large optical depths.
Method 4: Beer–Lambert Law
This law is a great simplification of the RTE but still provides an accurate solution if the following conditions are fulfilled:
- The radiation source is described by collimated, almost monochromatic beams
- Refraction, reflection, or scattering in the medium can be neglected
- There is no emission in the wavelength range of the incident beam
This is the case for photometry and the analysis of chemical compositions. The RTE then simplifies to:
(13)
with the beam’s orientation \mathbf{e}_i.
As the beam travels through the medium, energy is absorbed and the radiative heat source term is defined by:
(14)
Hence, the Beer–Lambert law describes the attenuation of the radiation intensity by absorption as the beam travels through the medium.
Verification Examples: Accounting for Radiation in Participating Media
This section shows examples for the different methods we discussed earlier and compares the results for various properties of the participating medium.
Cooling Glass Melt
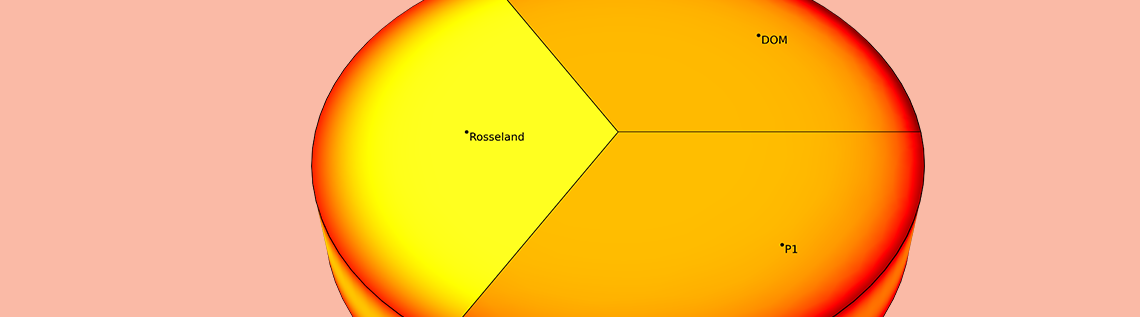
To compare the DOM, P1 approximation, and Rosseland approximation for a typical scenario, let’s take a look at a glass melt that is cooled down from 600°C to 20°C. Due to the high temperatures, this cooling occurs mainly via radiation. The resulting temperature distribution after 10 seconds is compared for low and high absorption coefficients.
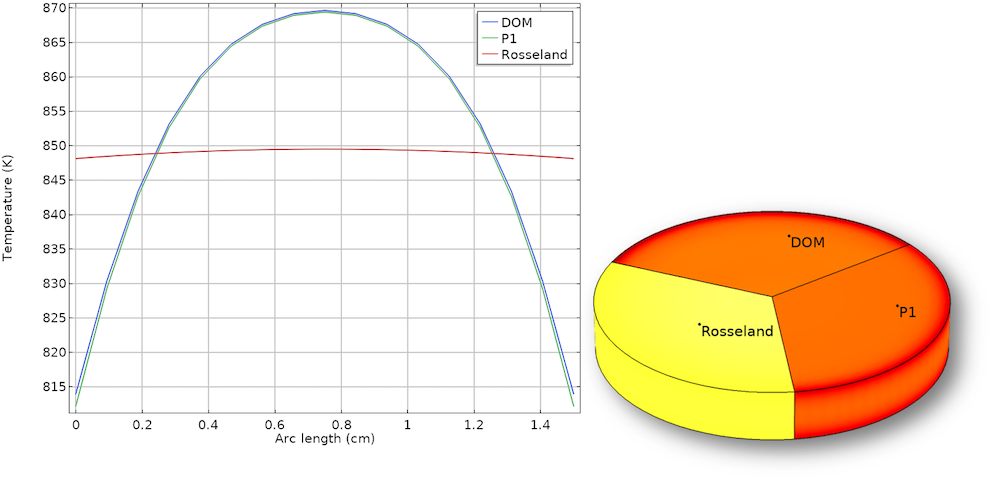
Temperature profile at the centerline and in the glass plate for \kappa=5\ m^{-1}. The Rosseland approximation is not sufficient for a low optical thickness. The P1 approximation provides a very accurate solution.
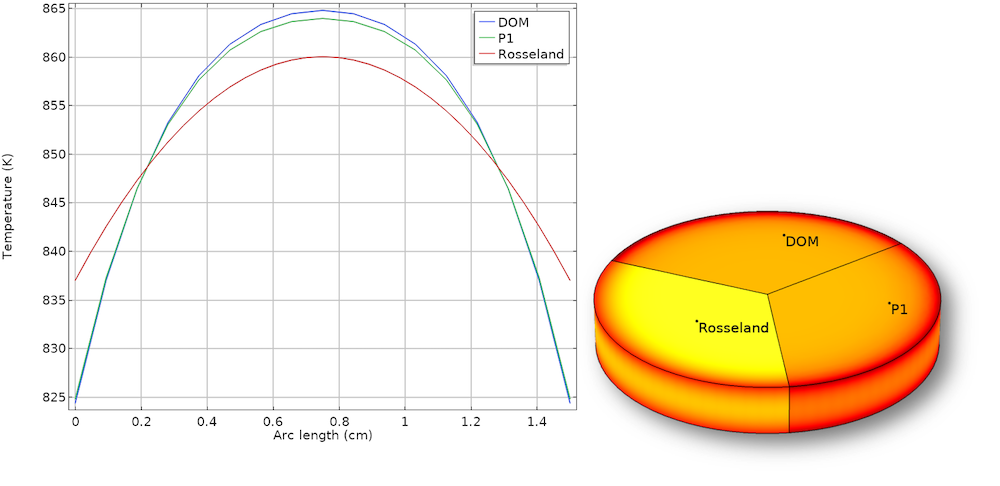
Temperature profile at the centerline and in the glass plate for \kappa=120\ m^{-1}. The Rosseland approximation provides a reasonable result despite its simplicity. The P1 approximation is still very accurate but not as accurate as it is for a low \kappa.
This example shows that the P1 approximation can be very accurate over a large range of \tau and gives good results for optically thin media as well. It also shows the weakness of the Rosseland approximation for small optical depths that are present at the walls and for a low \kappa. The computational costs for the DOM are significantly higher, taking about 10 times longer to solve than the other methods.
Scattering in a Cylinder
To investigate the accuracy of the P1 approximation and DOM for different scattering effects and wall properties, a verification model is investigated for three different cases:
- Constant surface emissivity, \epsilon_r=0.5, with isotropic scattering
- Radially varying emissivity, \epsilon_r=0.5(1-y/R), with isotropic scattering
- Radially varying emissivity, \epsilon_r=0.5(1-y/R), with linear anisotropic scattering
The scattering albedo \omega=\sigma / (\sigma+\kappa) is used to parameterize the model.
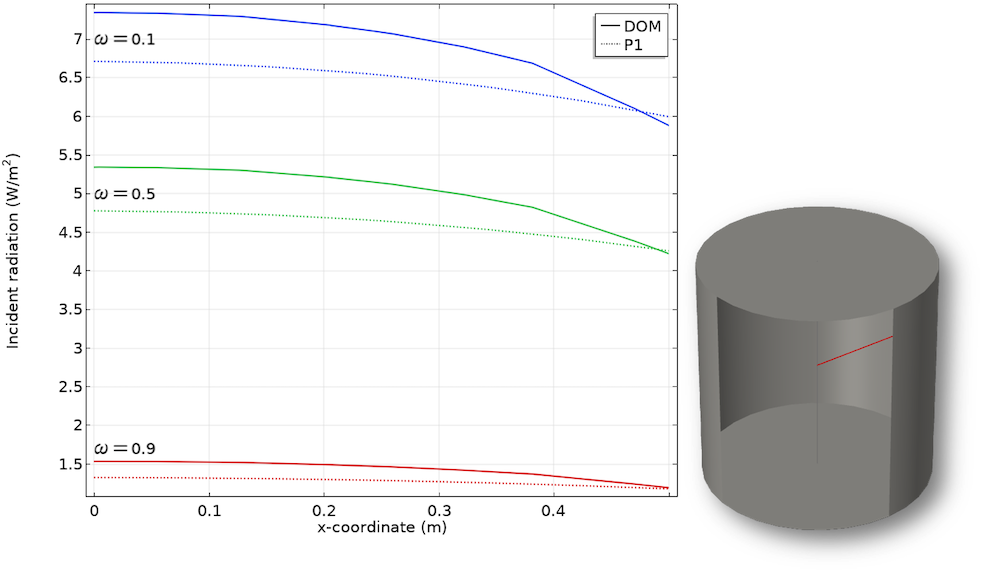
Case 1: Incident radiation for a varying isotropic scattering albedo in the radial direction.
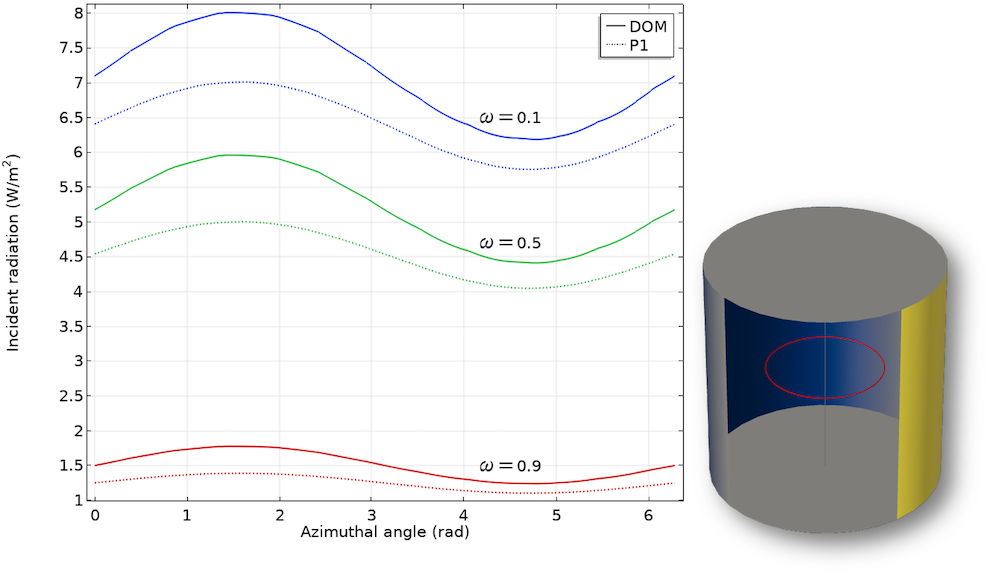
Case 2: Incident radiation for a varying isotropic scattering albedo in the azimuthal direction.
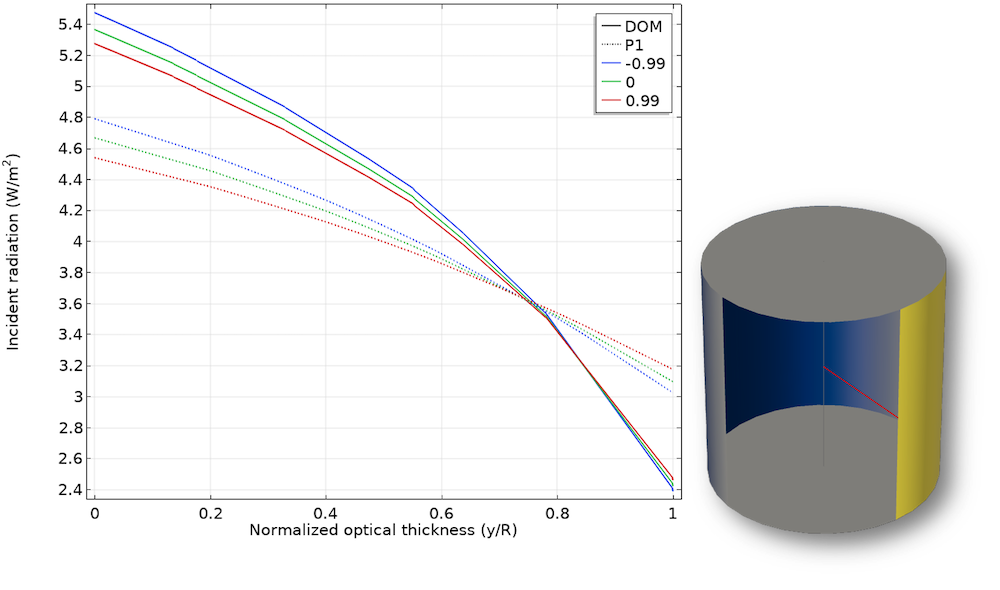
Case 3: Incident radiation for a varying linear anisotropic scattering along the normalized optical thickness.
This example shows that the P1 approximation approaches the accurate DOM solution for larger optical thicknesses for \omega \rightarrow 1. The error for small optical thickness increases. In particular, for linear anisotropic scattering (case 3), the method reproduces the results only roughly. Nevertheless, the P1 method is still a good approximation, especially if you consider the lower computational effort.
Concluding Thoughts on the Methods in COMSOL Multiphysics®
The methods we discussed cover the entire range of methods for computing radiation in participating media under different assumptions. To conclude this blog post, we summarize our findings for each method:
- DOM
- Is the most versatile method, solving the full RTE in discrete directions (up to 512) and providing high accuracy
- Can include complex forms of anisotropic scattering
- Computational costs increase as the number of discrete ordinates increase
- P1 method
- Is reasonably accurate for many configurations where the directional aspect of the radiation propagation does not dominate
- Can only include isotropic and linear anisotropic scattering
- Is computationally inexpensive by adding only one additional scalar equation to the system
- Rosseland approximation
- Provides good results for very large optical depths
- Cannot consider scattering
- Is computationally inexpensive by using a radiative conductivity in the heat transfer equation
- Beer-Lambert law
- Provides good results for applications that fulfill the assumptions for the underlying theory
- Has a narrow range of applications
- Is computationally inexpensive
Additional Resources
For more information about the functionality available for heat transfer modeling, click the button below to go to the Heat Transfer Module product page.
Learn more about modeling radiation by checking out the following tutorials:
Reference
- M.F. Modest, Radiative Heat Transfer, Academic Press, 2003.




Comments (0)