
When performing a tensile test on a specimen with a certain geometry and a ductile material, a phenomenon called necking can occur. At a certain load, the deformation is no longer homogeneous, and a localized “neck” develops. Engineers can use simulation to predict when it will occur. In a benchmark model illustrating the necking of an elastoplastic metal bar, the COMSOL® software is used to solve the numerical model, the results of which have been validated by published research.
Performing Uniaxial Tests on Elastoplastic Materials
Structural materials such as metals are subject to deformation, or changes in their shape or size, due to an applied force. In some materials, if the load is fairly small, then the deformation is only temporary and the material bounces back to its original shape. This behavior is called elastic deformation. However, as the load increases in the same material, the deformation can be permanent, which is called plastic deformation. Materials that are subject to this behavior are elastoplastic materials.
It’s important for engineers to test the strength of elastoplastic materials and evaluate the potential for deformation. One way to do this is through a type of material testing called a tensile (pulling force) test, which is a common method for obtaining the stress-strain relation of a solid material.
Uniaxial testing is the most popular method, thanks to a device that makes it easy to design such experiments: the Universal Testing Machine (UTM). This machine is “universal” in the sense that it is extremely versatile when it comes to the tests you can perform on various structures and materials.

The results of a tensile test of a ductile-fracture-type alloy, in which local necking can be seen. Image by Sigmund — Own work. Licensed under CC BY-SA 3.0, via Wikimedia Commons.
In a typical UTM, a flat or cylindrical test specimen is used. In this case, let’s say the metal bar is made of a ductile material. If the UTM pulls the ductile specimen to collapse, then a local decrease of the thickness or diameter of the bar can be observed prior to failure. The result is an instability phenomenon called necking, which is when the cross-sectional area of the material starts to decrease.
The tensile test is usually performed under displacement control. The force in the specimen is recorded, and the force can actually decrease because of the decrease in the cross section due to the necking. These control conditions are important, because if the test was performed under force control (say, by adding weight to the specimen), the bar would snap as soon as the peak load is reached.
A Quick Look at the Theory Behind Necking Instability
Necking can appear anywhere along a test specimen. The location is controlled by small deviations in diameter, material properties, and alignment of the testing machine. It is possible to analytically estimate when necking will occur. Since it is preceded by large plastic deformations, and plastic deformation of metals occurs without volume change, you can assume that the product of current length and current cross-sectional area gives a constant volume:
Here, the subscript 0 indicates the original values.
Thus, a small increase in length dL must be accompanied by a small (negative) change in area dA, such that
An increment in true (logarithmic) strain is defined as
The true stress is defined as the force divided by the current area
The necking starts when the force can no longer increase because the area decreases faster than the hardening of the material; that is, when
Thus, the instability criterion is:
Finally, we arrive at an amazingly simple criterion for the onset of necking:
So, when the slope of the stress-strain curve becomes equal to (or smaller than) the value of the current stress, necking instability occurs.
Interestingly enough, the maximum force in the tensile test is used to define the ultimate tensile strength of a material. However, the ultimate tensile strength is not a true property of the material, but rather a combination of the material properties and the geometry of the test specimen.
To model the necking effect in a metal bar subject to a tensile test, you can use COMSOL Multiphysics® and the add-on Nonlinear Structural Materials Module.
The necking of an elastoplastic metal bar. This simulation was created from a tutorial model that demonstrates the large-strain plasticity option available in the COMSOL® software.
Simulating the Necking of an Elastoplastic Metal Bar with the COMSOL® Software
In the Necking of an Elastoplastic Metal Bar benchmark example for large-strain plasticity codes, you can accurately simulate necking phenomenon and its growth in an elastoplastic material and compare the change in radius with results found in literature.
During a uniaxial test, when the load on the test specimen is increased to a certain amount, the bar goes through plastic deformation and, in later stages, necking in its central cross section.
This model is set up so that a cylindrical steel bar (with a height of 53.334 mm and a radius of 6.413 mm) is subjected to a total elongation of 14 mm. Since the problem shows 2D axial symmetry, you can reduce the geometry to a rectangle with width equal to the bar radius. The height of the model is equal to half of the bar length due to the symmetry in the axial direction, as shown below:
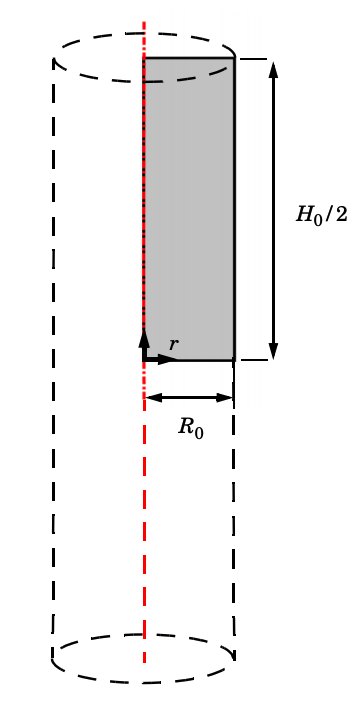
Schematic of the numerical model; the red line shows the rotation symmetry axis.
You can also set up the boundary conditions for the displacements in the radial and axial directions as well as impose the tensile loading through a prescribed elongation.
Next, the elastic behavior of the material can be characterized by Young’s modulus, E = 206.9 GPa, and Poisson’s ratio, v = 0.29. Then, the yield stress and hardening function can be set up using the constants and the nonlinear isotropic hardening model given in the documentation for the Necking of an Elastoplastic Metal Bar model. The nonlinear hardening is shown as a function of equivalent plastic strain in this plot:
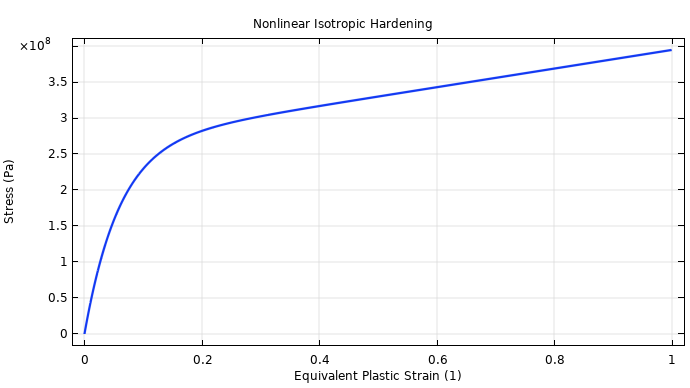
Nonlinear isotropic hardening as a function of equivalent plastic strain.
Evaluating the Simulation Results
After the metal bar undergoes large plastic strains at the symmetry plane, the results show that a 14-mm elongation (shown below as 7 mm for the half we are modeling) causes an effective plastic strain larger than 1.6 (160%) in the most affected region. You can see this region below in red, where the bar begins to contour as part of the necking effect.
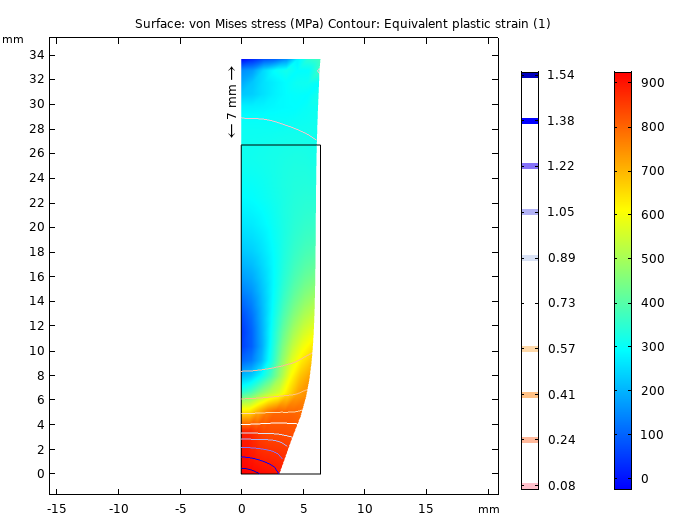
Von Mises stress and equivalent plastic strain at 7-mm end displacement.
Next, let’s take a look at the change in radius. First, the radius decreases linearly with the applied displacement. Then, once an axial displacement of about 3 mm occurs, the radius decreases more sharply, indicating that the metal bar is undergoing necking.
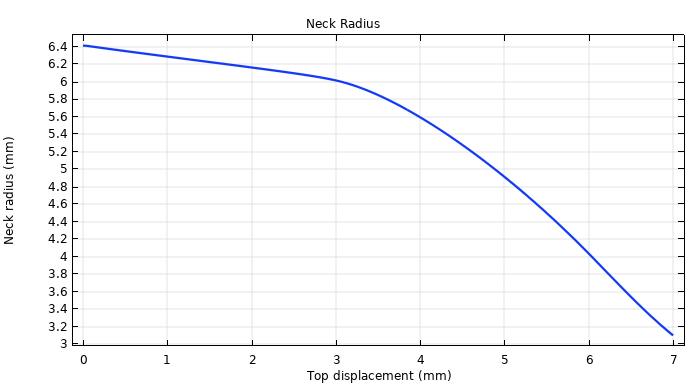
Necking development in the midsection of the bar.
These results are in good agreement with published research, showing that the COMSOL® software can accurately simulate a uniaxial test and illustrate the necking phenomenon in an elastoplastic material.
Next Step
Try modeling the necking of an elastoplastic metal bar yourself by clicking the button below. Doing so will take you to the Application Gallery, where you can download the tutorial documentation and the MPH-file.





Comments (1)
Said Bouta
August 9, 2023Please, How to obtain the crack of the specimen of this example?