
Wie man eine parametrisierte Geometrie einer Archimedischen Spirale erstellt
Archimedische Spiralen werden häufig bei der Analyse von Induktionsspulen, Spiralwärmetauschern und mikrofluidischen Geräten verwendet. Heute zeigen wir, wie man eine Archimedische Spirale mithilfe analytischer Gleichungen und ihrer Ableitungen erstellt, um eine Reihe von Spiralkurven zu definieren. Auf der Grundlage dieser Kurven werden wir dann eine 2D-Geometrie mit einer bestimmten Dicke erstellen und sie zu einer vollständigen 3D-Geometrie extrudieren.
Eine kurze Einführung zu Archimedischen Spiralen
Spiralen sind in der Natur weit verbreitet und werden in vielen technischen Konstruktionen verwendet. Als Elektroingenieur können Sie beispielsweise induktive Spulen spiralförmig wickeln und spiralförmige Antennen entwerfen. Als Maschinenbauingenieur können Sie Spiralen bei der Konstruktion von Federn, Schrägzahnrädern oder sogar bei dem unten abgebildeten Uhrwerk verwenden.

Ein Beispiel einer in einem Uhrwerk verwendeten Archimedischen Spirale. Bild von Greubel Forsey. Lizensiert durch CC BY-SA 3.0, via Wikimedia Commons.
Wir werden uns hier auf eine bestimmte Art von Spirale konzentrieren, nämlich die, die in dem oben gezeigten Mechanismus vorkommt: die Archimedische Spirale. Eine Archimedische Spirale ist eine Art von Spirale, die einen festen Abstand zwischen ihren aufeinanderfolgenden Windungen hat. Aufgrund dieser Eigenschaft wird sie häufig für die Konstruktion von flachen Spulen und Federn verwendet.
Wir können eine Archimedische Spirale mit der folgenden Gleichung in Polarkoordinaten beschreiben:
wobei a und b Parameter sind, die den anfänglichen Radius der Spirale und den Abstand zwischen ihren aufeinanderfolgenden Windungen definieren, wobei letzterer gleich 2 \pi b ist. Man beachte, dass eine Archimedische Spirale manchmal auch als arithmetische Spirale bezeichnet wird. Dieser Name leitet sich von der arithmetischen Folge des Abstands vom Ursprung zu einem Punkt auf derselben Radialen ab.
Die parametrisierte Geometrie einer Archimedischen Spirale entwerfen
Nachdem wir nun die archimedischen Spiralen vorgestellt haben, wollen wir uns ansehen, wie man eine solches Design für die Analyse in COMSOL Multiphysics® parametrisiert und erstellt.
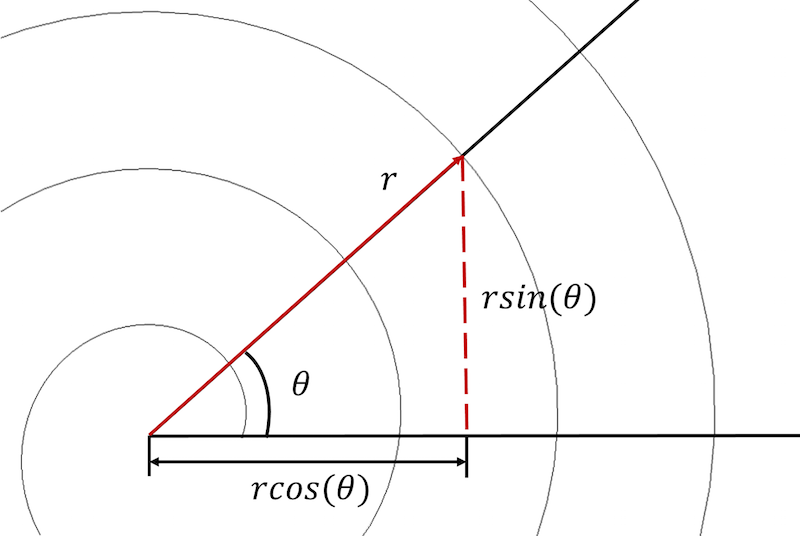
Eine Archimedische Spirale kann sowohl ich Polar- als auch in kartesischen Koordinaten beschrieben werden.
Zuerst müssen wir die Spiralgleichungen von einem polaren in ein kartesisches Koordinatensystem umwandeln und jede Gleichung in parametrischer Form ausdrücken:
x_{Komponente}=rcos(\theta) \\
y_{Komponente}=rsin(\theta)
\end{align*}
Diese Transformation ermöglicht es uns, die Gleichung der Archimedischen Spirale in eine parametrischen Form im kartesischen Koordinatensystem umzuformulieren:
x_{Komponente}=(a+b\theta)cos(\theta) \\
y_{Komponente}=(a+b\theta)sin(\theta)
\end{align*}
In COMSOL Multiphysics® müssen eine Reihe von Parametern bestimmt werden, die die Geometrie der Spirale definieren. Diese Parameter sind der Anfangsradius der Spirale a_{initial}, der Endradius der Spirale a_{final} und die gewünschte Anzahl der Windungen n. Die Wachstumsrate der Spirale b kann dann ausgedrückt werden als:
Außerdem müssen wir den Startwinkel theta_0 und den Endwinkel theta_f der Spirale bestimmen. Beginnen wir mit den Werten von theta_0=0 und theta_f=2 \pi n. Mit diesen Informationen sind wir in der Lage, eine Reihe von Parametern für die Spiralgeometrie zu definieren.
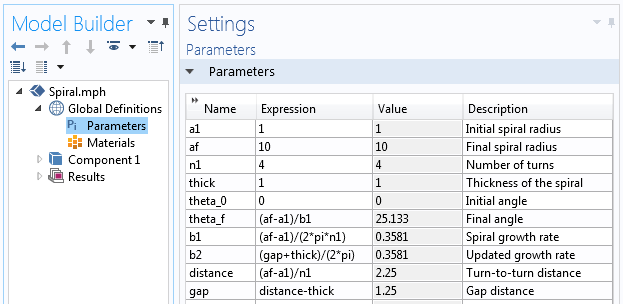
Die für die Spiralgeometrie verwendeten Parameter.
Um diese Spirale zu erstellen, beginnen wir mit einer 3D Component und erstellen eine Work Plane im Bereich Geometry. In der Geometrie der Work Plane fügen wir dann eine Parametric Curve hinzu und verwenden die oben genannten parametrischen Gleichungen mit einem variablen Winkel, um eine 2D-Version der Archimedischen Spirale zu zeichnen. Diese Gleichungen können direkt in das Feld der parametrischen Kurve eingegeben werden, oder wir können zunächst jede Gleichung in einer neuen Analytic Funktion wie folgt definieren:
X_{fun}=(a+bs)cos(s) \\
Y_{fun}=(a+bs)sin(s) \\
\end{align*}
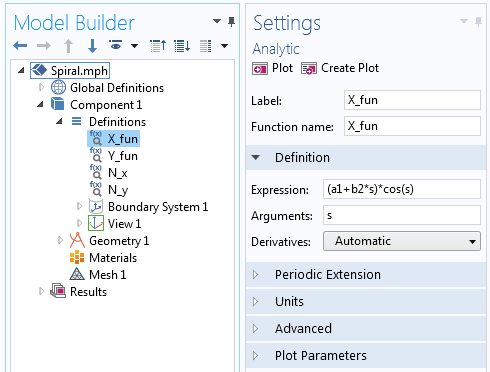
Die X-Komponente der in der Analytic Funktion definierten Gleichung für die Archimedischen Spirale.
Die Analytic Funktion kann in den Ausdrücken für die parametrische Kurve verwendet werden. In dieser parametrischen Kurve variieren wir den Parameter s vom Anfangswinkel der Spirale, theta_0, bis zum Endwinkel der Spirale, theta_f=2 \pi n.
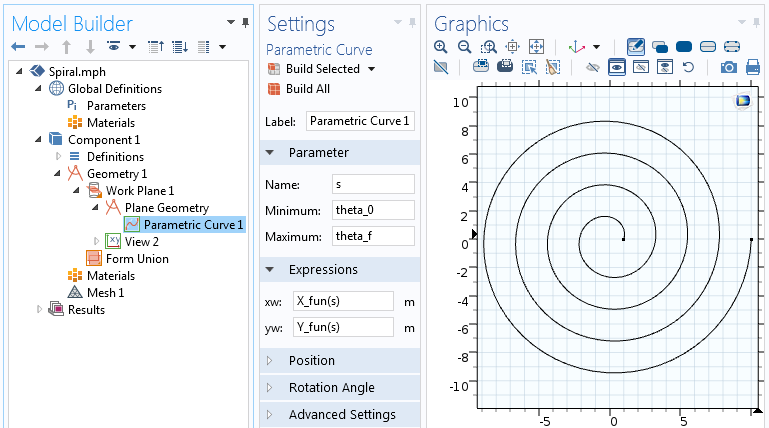
Die Einstellungen für das Feature Parametric Curve.
Die Gleichungen für parametrische Spiralen, die in der Funktion Parametric Curve verwendet werden, führen zu einer durch eine Kurve dargestellten Spirale. Bauen wir nun auf dieser Geometrie auf und fügen ihr eine Dicke hinzu, um ein festes 2D-Objekt zu erstellen.
Bis zu diesem Punkt wurde unsere Spirale durch den Anfangsradius a_{Anfang}, den Endradius a_{Ende} und die gewünschte Anzahl der Windungen n parametrisiert. Nun müssen wir die Dicke als weiteren Kontrollparameter in die Spiralgleichung einbeziehen.
Beginnen wir mit der Haupteigenschaft der Spirale, die besagt, dass der Abstand zwischen den Spiralwindungen gleich 2 \pi b ist. Dies ist auch äquivalent zu \frac{a_{final}-a_{initial}}{n}. Um die Dicke zu berücksichtigen, stellen wir den Abstand zwischen den einzelnen Windungen der Spirale als Summe der Spiralendicke und der verbleibenden Lücke zwischen den Windungen dar, Dicke+Lücke.
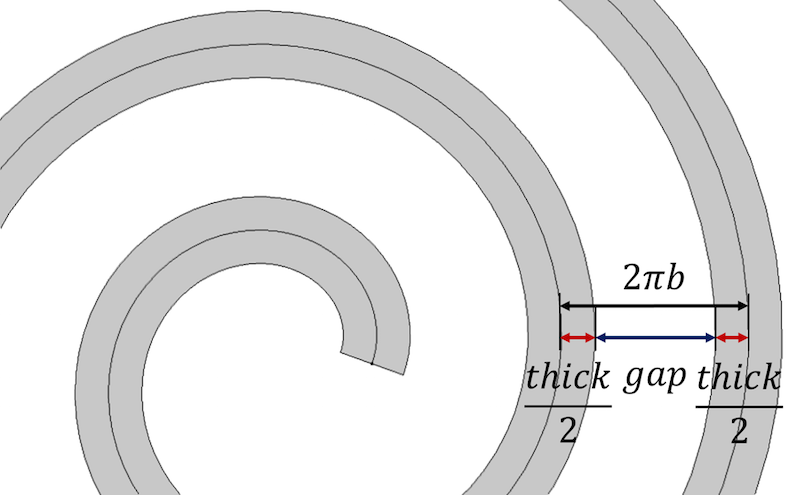
Der Abstand zwischen den Spiralwindungen ist über die Parameter Spiralendicke und Lücke definiert.
Um die Dicke zu kontrollieren und den gleichen Abstand zwischen den Windungen zu erhalten, kann der Abstand wie folgt beschrieben werden:
Abstand=\frac{a_{initial}-a_{final}}{n} \\
Lücke=Abstand-Dicke
\end{align*}
Nachdem wir die Dicke definiert und den Abstand zwischen den Windungen mittels der Dicke und konstantem Abstand zwischen den Mittellinien der Spirale ausgedrückt haben, können wir den Wachstumsparameter der Spirale mit der Dicke wie folgt beschreiben:
Abstand=2\pi b \\
b=\frac{Lücke+Dicke}{2\pi}
\end{align*}
Wir wollen auch den Endwinkel der Spirale mittels ihres Anfangs- und Endradius ausdrücken:
\theta_{final}=2 \pi n \\
a_{final}=\text{total distance}+a_{initial} \\
a_{final}=2 \pi bn+a_{initial} \\
n=\frac{a_{final}-a_{initial}}{2 \pi b} \\
\theta_{final}=\frac{2 \pi (a_{final}-a_{initial})}{2 \pi b} \\
\theta_{final}=\frac{a_{final}-a_{initial}}{b}
\end{align*}
Sollen Sie die Spirale mit einem anderen Winkel als Null beginnen? Wenn ja, müssen Sie im Ausdruck für den Parameter diesen Anfangswinkel zum Endwinkel hinzufügen: theta_f=\frac{a_{final}-a_{initial}}{b}+theta_0.
Wenn man die bestehende Spiralkurve zweimal dupliziert und diese Kurven mit einem Versatz von -\frac{Dicke}{2} und +\frac{Dicke}{2} in Bezug auf die ursprüngliche Spiralkurve platziert, kann man die Spirale mithilfe der Dicke aufbauen. Um die obere und untere Spirale richtig zu positionieren, müssen wir sicherstellen, dass die versetzten Spiralen senkrecht zur anfänglichen Spiralkurve stehen. Dies kann erreicht werden, indem man den Versatzabstand \pm\frac{Dicke}{2} mit dem Einheitsvektor senkrecht zur Spiralkurve multipliziert. Die Gleichungen der Normalenvektoren zu einer Kurve in parametrischer Form sind:
wobei s der Parameter ist, der in der Funktion Parametric Curve verwendet wird. Um eine Einheitsnormale zu bekommen, müssen wir diese Ausdrücke durch die Länge der Normalen teilen:
Unsere angepassten parametrischen Gleichungen für die Archimedische Spirale mit einer Verschiebung um die halbe Dicke sind:
x_{Komponente}=(a+bs)cos(s)-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{Dicke}{2} \\
y_{Komponente}=(a+bs)sin(s)+\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{Dicke}{2}
\end{align*}
Das Aufschreiben dieser Gleichungen in den Ausdrucksfeldern der parametrischen Kurve kann recht zeitaufwändig sein. Aus diesem Grund führen wir die folgende Notation ein:
N_x=-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}} \\
N_y=\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2 }}
\end{align*}
wobei jedes N_x und N_y über die Funktion Analytic in COMSOL Multiphysics® definiert wird, ähnlich wie wir X_{fun} und Y_{fun} für die erste parametrische Kurve definiert haben. Innerhalb der Funktion verwenden wir den Differenzierungsoperator d(f(x),x), um die Ableitung zu bilden, wie im folgenden Screenshot zu sehen ist.
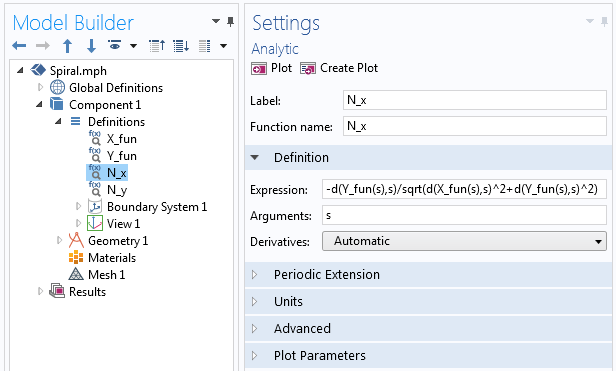
Beispiele für den in der Funktion Analytic verwendeten Differenzierungsoperator.
Die Funktionen X_{fun}, Y_{fun}, N_x und N_y können dann direkt in den Ausdrücken der parametrischen Kurve für die Kurve auf einer Seite verwendet werden:
x_{unten}=X_{fun}(s)+N_x(s)\frac{Dicke}{2} \\
y_{unten}=Y_{fun}(s)+N_y(s)\frac{Dicke}{2}
\end{align*}
Die Funktionen können auch für die Kurve auf der anderen Seite verwendet werden:
x_{oben}=X_{fun}(s)-N_x(s)\frac{Dicke}{2} \\
y_{oben}=Y_{fun}(s)-N_y(s)\frac{Dicke}{2}
\end{align*}
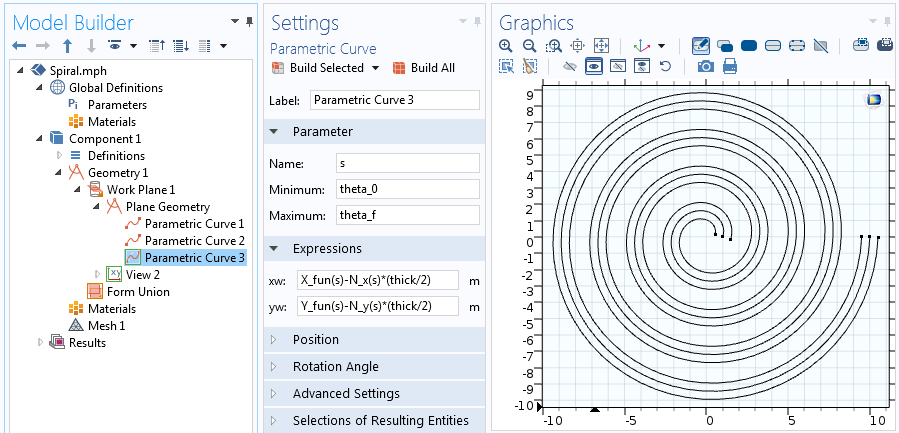
Gleichungen für die zweite der beiden versetzten parametrischen Kurven.
Um die Enden der beiden Kurven zu verbinden, fügen wir zwei weitere parametrische Kurven hinzu, indem wir die oben genannten Gleichungen leicht abändern. Für die Kurve, die die Mitte der Spirale verbindet, müssen wir X_{fun}, Y_{fun}, N_x und N_y für den Anfangswert des Winkels, theta, berechnen. Für die Kurve, die die äußere Seite der Spirale verbindet, müssen wir den Endwert von theta ermitteln. Die verbindende Kurve in der Mitte ist also:
X_{fun}(theta_0)+s\cdot N_x(theta_0)\cdot\frac{Dicke}{2} \\
Y_{fun}(theta_0)+s\cdot N_y(theta_0)\cdot\frac{Dicke}{2}
\end{align*}
Die äußere verbindende Kurve ist dabei:
X_{fun}(theta_f)+s\cdot N_x(theta_f)\cdot\frac{Dicke}{2} \\
Y_{fun}(theta_f)+s\cdot N_y(theta_f)\cdot\frac{Dicke}{2}
\end{align*}
In beiden obenstehenden Gleichungen liegt s im Bereich von -1 bis +1, wie im folgenden Screenshot zu sehen ist.
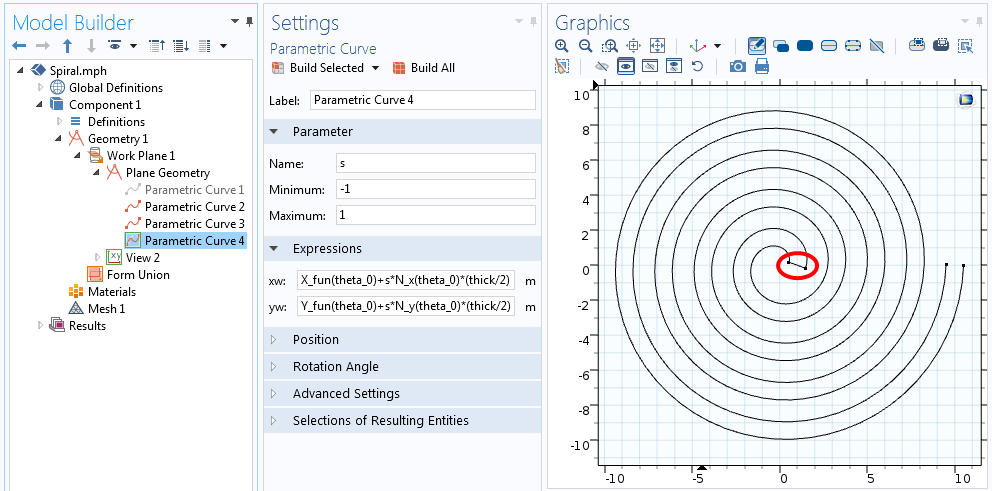
Gleichungen für die Kurve, die ein Ende der Spirale verbindet.
Wir haben jetzt fünf Kurven, die die Mittellinie der Spirale und alle vier Seiten des Profils definieren. Wir können die Kurve, die die Mittellinie beschreibt, deaktivieren (oder sogar löschen), da sie nicht wirklich notwendig ist, so dass nur der Umriss der Spirale übrig bleibt. Nachdem der Umriss unserer Spirale definiert ist, kann die Operation Convert to Solid verwendet werden, um ein einzelnes Geometrieobjekt zu erstellen. Diese 2D-Spirale kann schließlich über die Operation Extrude in 3D extrudiert werden.
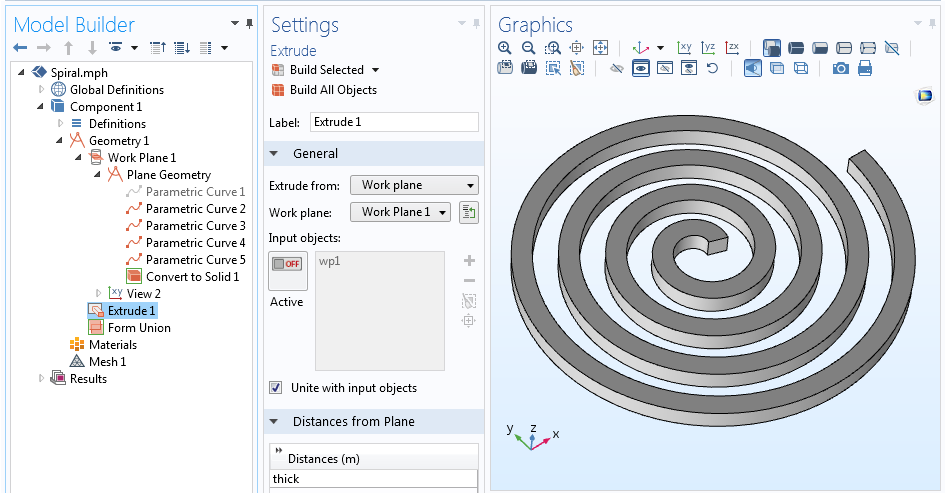
Die vollständige Geometriefolge und die extrudierte 3D-Geometrie.
Abschließende Bemerkungen zur Modellierung einer Archimedischen Spirale in COMSOL Multiphysics®
Wir haben Sie nun durch die Schritte zur Erstellung einer vollständig parametrisierten archimedischen Spirale geführt. Mit dieser Spiralgeometrie können Sie jeden der Parameter ändern und mit verschiedenen Designs experimentieren oder sie sogar als Parameter in einer Optimierungsstudie verwenden. Wir möchten Sie ermutigen, diese Technik in Ihren eigenen Modellierungsprozessen zu verwenden, um die Analyse Ihres speziellen spiralbasierten Konstruktionsentwurfs voranzutreiben.
Weitere Ressourcen zu Design und Analyse von Spiralen
- Um weitere Anwendungen der Simulation zur Gestaltung von Spiralmodellen zu erkunden, probieren Sie dieses Tutorial-Modell aus: Spiral Slot Antenna
- Oder lesen Sie eine Anwendergeschichte zum Thema: “Analysis of Spiral Resonator Filters”




Kommentare (0)