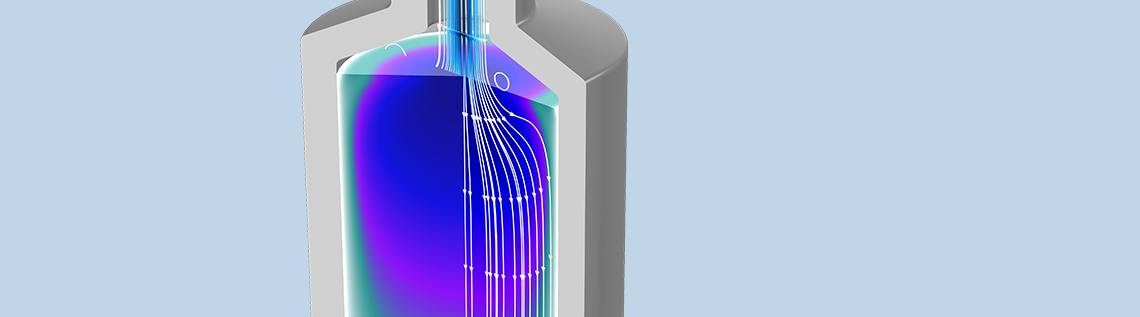
The need for advanced porous media modeling spans many industries. The Porous Media Flow Module, an add-on to the COMSOL Multiphysics® software available as of version 5.5, was made for this: It lets you quantitatively investigate mass, momentum, and energy transport in porous media. Interest areas for this product include fuel cell processes, pulp and paper drying, the production of food, filtration, and many more.
Modeling Porous Media Flow
Simulating mass, momentum, and energy flow in porous media is common in a number of engineering fields, such as chemical, civil, and nuclear engineering. The Porous Media Flow Module provides a comprehensive set of physics interfaces to help engineers and scientists simulate different types of physical processes in porous media.
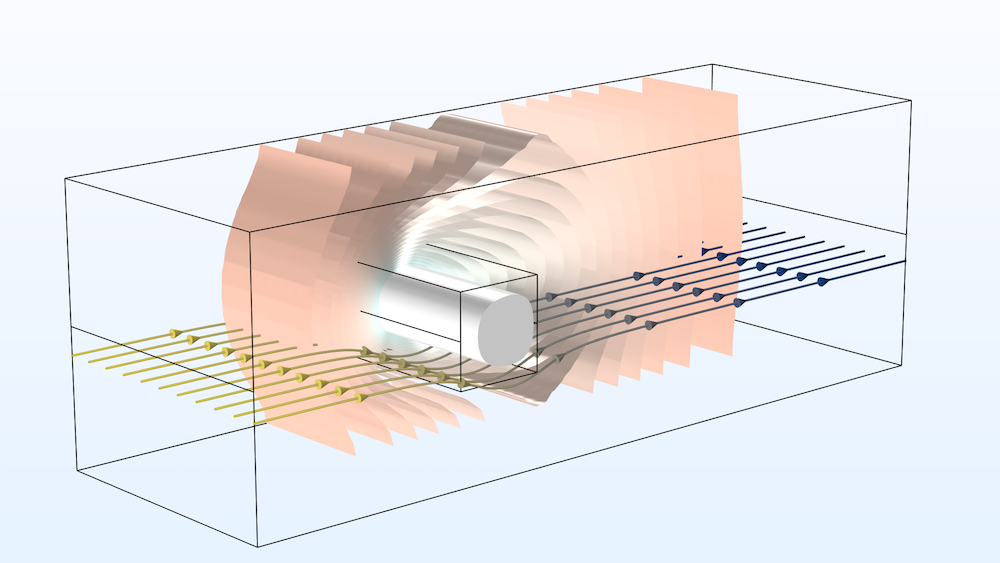
A frozen inclusion modeled using the Porous Media Flow Module.
The Porous Media Flow Module allows engineers within many different industries, such as mining, biomedicine, and the food industry, to analyze and optimize their processes in a user-friendly environment. Applications such as multiphase transport in porous media can be addressed within a fully multiphysics approach.
With the multiphysics capabilities of the Porous Media Flow Module, you can compute:
- Nonisothermal flow in a porous medium
- Effective properties for a multicomponent system
- Poroelasticity
- The transport of moisture and chemical species
Let’s take a look at a few of these application areas in more detail…
Multiphase Transport in Porous Media
The Porous Media Flow Module includes tools that can be used to simulate multiphase flow in porous media with two or any number of moving phases. You can specify porous media properties such as relative permeabilities and capillary pressures between phases to model wicking, moisture transport, or other transport phenomena in porous media.
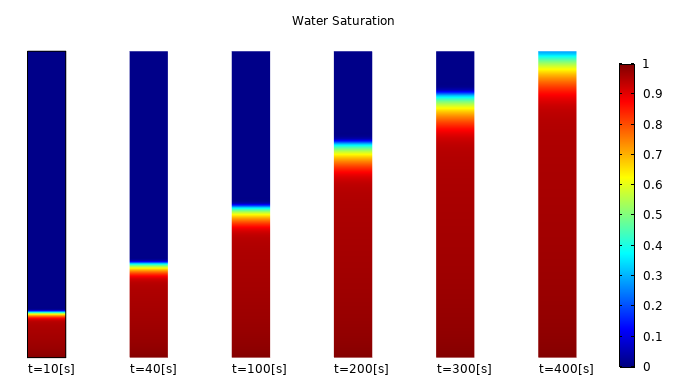
A model showing wicking in a paper strip, a porous medium.
When a dry strip of paper is put into contact with a fluid, it will absorb it due to capillary forces. Absorption will continue until gravitational forces balance the capillary forces. In this example, two phases, water and air, interact through the combination of the Darcy’s Law and Phase Transport in Porous Media interfaces.
Non-Darcian Flow in Porous Media
In a previous blog post, we discuss physics interfaces available for simulating flow in saturated and variably saturated porous media, including the Darcy’s Law and Brinkman Equations interfaces.
Darcy’s law applies to low interstitial velocity in the pores, which typically means Reynolds numbers below 100. For higher velocities and Reynolds numbers, an additional nonlinear correction can be added to the momentum equation. The Porous Media Flow Module includes the possibility to model non-Darcian flows, where the velocity field is nonlinear with respect to the pressure drop.
The available options to model non-Darcian flow in porous media are the Forchheimer, Ergun, Burke–Plummer, and Klinkenberg models for the Darcy’s Law and Multiphase Flow in Porous Media interfaces; and Forchheimer and Ergun models for Brinkman equations.
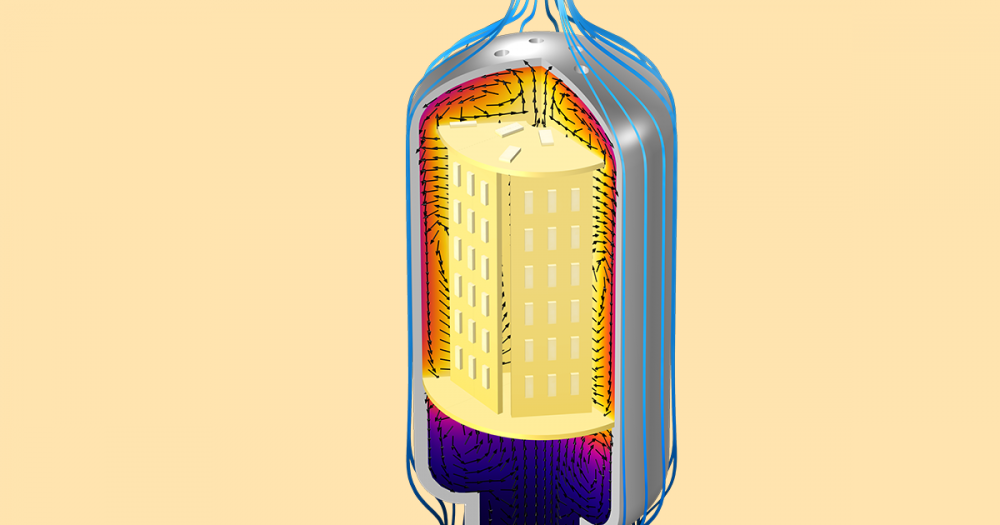
Local Thermal Equilibrium and Nonequilibrium for Heat Transfer in Porous Media
Heat transfer in porous media may occur due to conduction, convection, and dispersion, and it must take into account the different thermal properties of solid and fluid phases. With the Porous Media Flow Module, it’s possible to model heat transfer in porous structures using two modeling approaches:
- Local thermal equilibrium (LTE), where the temperature of the solid matrix and the fluid phase are in local equilibrium
- Local thermal nonequilibrium (LTNE), where distinct energy equations are formulated for the solid and fluid phases, and it is important to take into account for the heat transfer at the fluid-solid interface

A model of a packed bed latent heat storage unit including phase change effects and local thermal nonequilibrium.
Fracture Flow in Porous Media
Modeling mass momentum and energy transport in fractured porous media is relevant to chemical, civil, and nuclear engineers, to name a few. The Porous Media Flow Module includes physics interfaces to model pressure, temperature, and chemical species transport on internal boundaries within a porous matrix. This approximation saves you from meshing the actual fractures and the computational resources this entails.

A model of a ceramic water filter with an activated carbon core.
Ceramic water filters are commonly used to remove chemicals and particles from drinking water. The small pores in the ceramic core remove large particles and bacteria, and the activated carbon can also remove heavy metals and chlorine. Cracks in the ceramic core might result in remaining pollutants in the drinking water.
Phase Change in Porous Media
The Porous Media Flow Module also includes a tailored interface to model phase change in porous media. Typical phase transition phenomena include the melting of ice into water or the evaporation and condensation of vapor in building materials.
Next Step
Find out more about the dedicated functionality for modeling mass, momentum, and energy transport in porous media in the Porous Media Flow Module by clicking the button below:



Comments (8)
Ziad Saghir
June 26, 2020Dear Dr Gonzales
I am studying forced convection in a porous block using nanofluid. I solved the problem using single fluid approach and results in agreement with the experiment conducted in my lab. I am interested in solving the problem in using two phase flow approach. My porosity is 0.91. Which comsol module do you recommend. I successfully used Darcy law but my problem require viscous effect like Darcy Brinkman. Please advise
Best regards
Ziad Saghir(email: zsaghir@ryerson.ca)
Ed Gonzalez
June 29, 2020 COMSOL EmployeeHi Ziad,
Please contact your local COMSOL office using https://www.comsol.com/contact and describe your application, and one of my colleagues will contact you to discuss the details.
Greetings
Ed
Yousif Muhammad
June 29, 2020Thanks for the great blog, I have been using “Local Thermal Equilibrium and Nonequilibrium for Heat Transfer in Porous Media” module for my thermal energy storage project.
Vikash Kumar
March 15, 2021Hi Gonzalez
In the model for three-phase flow, how the equation can be modified. The below equation is valid for two phases, which is air (s2) and water(s1). what if I have third phase(s3, let say glycerin)
P0 = -(phtr.pc_s2)*step1(s1)-rho_air*L0*g_const
Ed Gonzalez
March 16, 2021 COMSOL EmployeeDear Vikash,
You can model multiphase flow in porous media (three or more phases) with the help of the Phase Transport in Porous Media interface. Please contact our support team at https://www.comsol.com/support
Vikash Kumar
August 21, 2021Dear Gonzalez, I contact comsol support, but they couldn’t able to help me. If you can suggest a solution, it would highly appreciable
Vikash Kumar
August 21, 2021Dear Gonzalez, The Brooks, and Corey model are applicable for two phases, for three phases no such model is available. Could you please suggest some model.
Vikash Kumar
September 9, 2021Dear Gonzalez
Kindly support me. My mail id is vikashkumar0603@gmail.com I would be highly obliged