
When the Newtonian telescope was first developed in 1668, it was recognized as the earliest operating reflecting telescope. With its low cost and simplistic design, this optical system became a favorable alternative to refracting telescopes, and the technology continues to be widely used today. Using the Ray Optics Module, we can analyze ray propagation within this type of telescope system.
Pause and ‘Reflect’
The first practical refracting telescope appeared in the year 1608. As indicated by its name, this technology forms images through refraction, the change in direction of light as it crosses between two media in which the speed of light is different. A simple refracting telescope uses a lens as an objective to collect and focus light. Noted as the first kind of optical telescope, this technology would later soar to popularity during the second half of the 19th century.
A problem with this device, however, arose in the form of chromatic aberration. This type of distortion results from the failure of a lens to focus all the colors at the same point of convergence. In refracting telescopes, the angle of refraction at each surface is dependent upon the wavelength, causing different wavelengths of light to be focused at varying points. This resulted in blurred images or fringes of color acting as a halo around objects.
While developing the theory of color, British scientist Sir Isaac Newton made a connection between this technical flaw in refracting telescopes and the prisms with which he was experimenting. He identified the telescope’s lens as the root of the issue. Like his prisms, the lens of the refracting telescope broke white light into a rainbow of colors surrounding large, bright objects.
With this discovery came a solution: create a telescope without using a lens as the objective. This brings us to the roots of the Newtonian telescope.
Developing the Newtonian Telescope
While building his first reflecting telescope, Newton chose to replace the primary lens with a metal mirror made of tin and copper. When selecting the shape of the objective mirror, he opted for a spherical shape in an effort to simplify the telescope’s design.
On his reflector, Newton chose to add a secondary diagonally mounted mirror. This component was placed near the primary mirror’s focus so as to reflect the image at a 90° angle to an eyepiece mounted on the telescope’s side. This design element was particularly significant as it enabled the image to be viewed with very little obstruction of the objective mirror.

A photo showing a replica of the second reflecting telescope developed by Newton and presented to the Royal Society of London in 1672. (“NewtonsTelescopeReplica” by Solipsist (Andrew Dunn). Licensed under Creative Commons Attribution Share-Alike 2.0, via Wikimedia Commons).
In addition to operating without color distortion, the optical device also enabled Newton to view the four Galilean moons of Jupiter as well as the crescent phase of Venus. While the technology impressed members of the Royal Society of London, the reflecting telescope was not widely adopted at first due to construction difficulties, which ranged from creating an effective reflector to surfaces that tarnished quickly.
Building on Newton’s design, John Hadley presented an improved version of the telescope to the Royal Society in 1721. The new version addressed several issues surrounding the development of a parabolic mirror.
Design Advantages
Along with eliminating chromatic aberration, many other advantages can be noted in the development of the Newtonian telescope. With this design, it became easier to achieve a short focal ratio, which in turn produced a wider field of view.
Additionally, the overall fabrication of the telescope was simpler as it required only one surface to be ground and polished into a rather complex shape. In comparison to its refractive counterpart, this reflecting telescope proved much more cost effective to produce.
Simulating the Ray Propagation of Unpolarized Light
From tracing origins to tracing rays — let’s now shift our focus to modeling the ray propagation of light within the Newtonian telescope system. This phenomenon can be analyzed by using the Newtonian Telescope model in the Ray Optics Module, new with COMSOL Multiphysics version 5.0.
In this example, the model telescope is comprised of two mirrors — a spherical primary mirror and a planar secondary mirror — and an ellipsoidal lens. Using the secondary mirror, a 45° angle is formed with the rays that are reflected from the primary mirror. Light is directed toward the ellipsoidal lens by the secondary mirror, forming images of the objects upon the focal surface. Here, the rays are released only from a subset of points on the telescope’s aperture in order to not be obstructed by the secondary mirror.
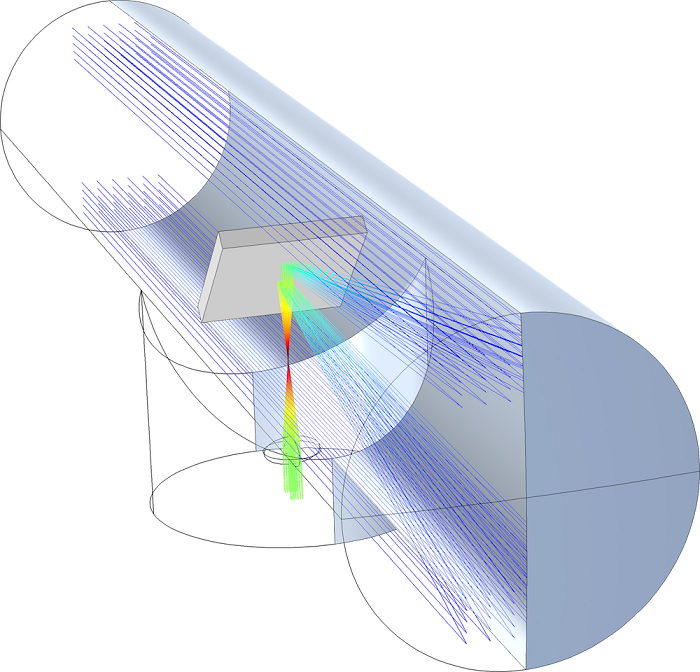
The trajectories and intensity of rays as they travel through the telescope.
To visualize the performance of the optical system design, this study utilizes a spot diagram. This plot indicates the points at which rays launched from the telescope’s aperture hit the image plane. Typically, designs of good quality should have spots appearing within a circle corresponding to the central diffraction spot from the aperture of the optical system.
The spot diagram uses a color expression to indicate the ratio between ray intensity in the image plane and initial intensity. As indicated in the diagram below, the rays arriving at the focal surface have an intensity that varies from 65.3 to 88.8 times greater than the initial intensity of the distributed rays.
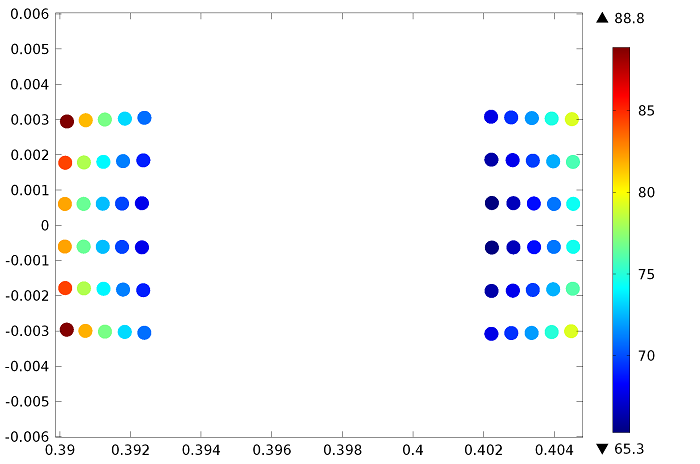
Spot diagram highlighting the ratio between ray intensity and initial intensity. Note that the dots in the diagram are symmetric about the x-axis but not the y-axis. This is attributed to the fact that the x-axis lies in the symmetry plane of the telescope.
Next Steps
- Download the Newtonian Telescope model
- Read more about the Ray Optics Module




Comments (0)