
Shape optimization can be used to enhance device design in many application areas, including electromagnetics and RF. In this blog post, we will provide two examples of how you can benefit from using shape optimization and show you what you can achieve when applying the shape optimization features in the COMSOL Multiphysics® software to microwave and millimeter-wave (mmWave) applications.
This is the second blog post in a two-part series on shape optimization in electromagnetics. The first blog post focuses on shape optimization in wave optics. Read Part 1 here.
Background Information
Before we dive into shape optimization, we should note why one may use it over parameter optimization. The key difference between shape and parameter optimization is that shape optimization works by deforming the mesh, which makes the mesh compatible with gradient-based optimization. This increases the efficiency of the method to the point where it’s possible to optimize thousands of control variables for a reasonable computational time on a standard workstation. While parameter optimization has its own benefits, it’s also slow because of its incompatibility with gradient-based optimization. As explained in the first post in this series, “Shape Optimization in Electromagnetics: Part 1”, this “limits the number of optimization variables, and thus the design freedom.” This is the primary reason why we are focusing on shape optimization in this series.
The examples shown here will be solved with the method of moving asymptotes (MMA) as the optimization algorithm. In particular, the globally convergent version of this method, GCMMA, will be used, as this tends to provide superior results for minimax problems. The method also supports move limits, which reduces the likelihood of issues with inverted elements. For these two reasons, it’s the preferred optimization method for most shape optimization problems. Note, however, that it’s also possible to perform optimization using second-order methods such as IPOPT or SNOPT, and, for simple problems, convergence can be faster than MMA.
Example 1: Filter
Let’s consider shape optimization by first looking at the Optimization of a Waveguide Iris Bandpass Filter — Transformation Version model as an example. It would be relatively simple to solve this problem using parameter optimization, but shape optimization is faster. This model is conceptually similar to the filter example in the first blog post, and both examples use the Transformation feature. The geometry in this example, however, is different, and a minimax objective is used:
where f_\mathrm{pass} is the pass frequency, and \mathrm{S11}_\mathrm{dB} and \mathrm{S21}_\mathrm{dB} are the logarithmic values of the S-parameters.
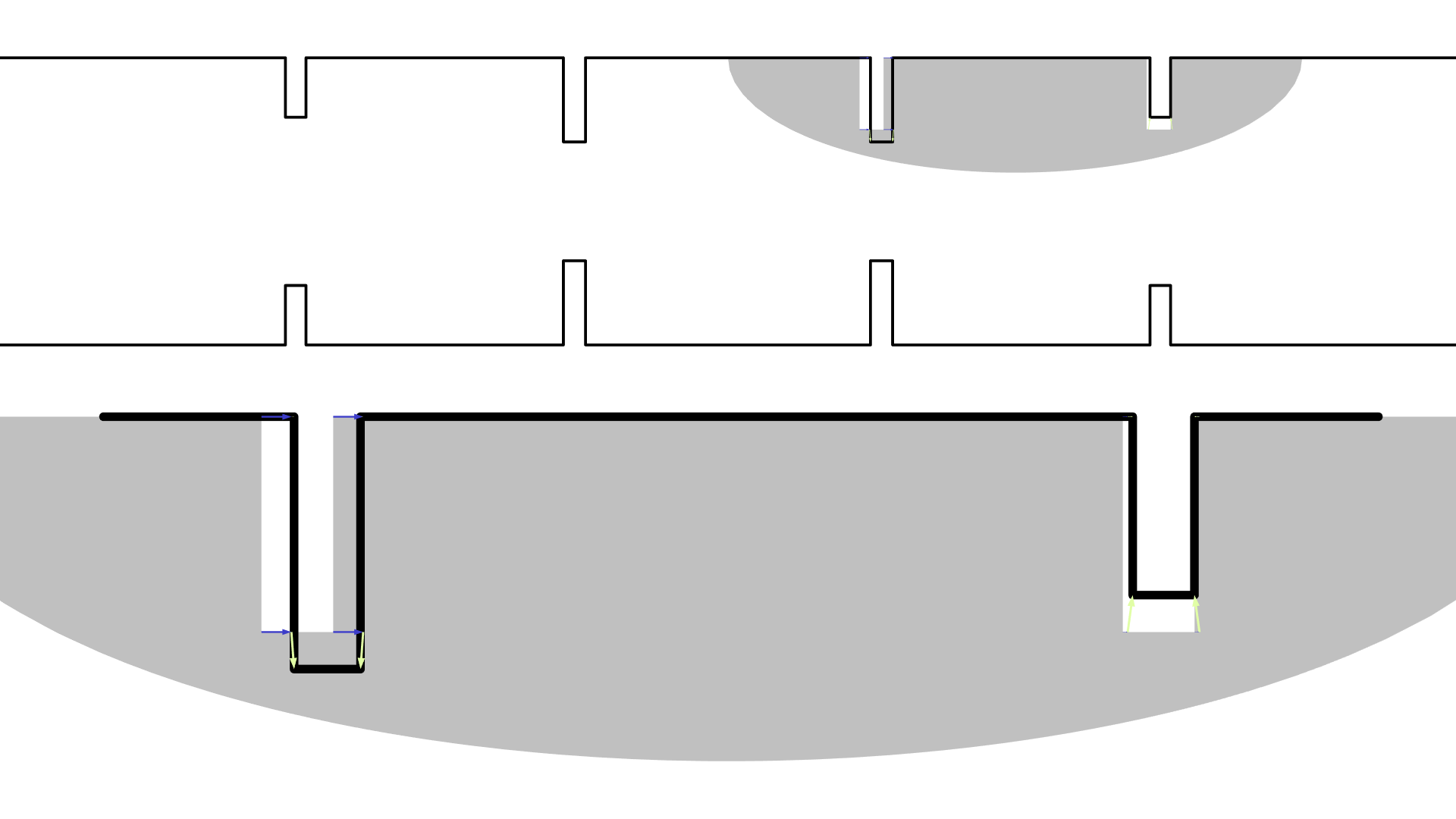
The geometry consists of four irises, and these are optimized by controlling the size of two of them with a Transformation feature. A Symmetry/Roller feature is used on adjacent boundaries so that the position of the irises can also be changed. Note that the two irises can vary independently of each other since the Transformation feature automatically splits the selection if it consists of different groups that do not share points. This is particularly convenient when there are many objects to be optimized, as demonstrated in the first part of this blog post series. In this example, the twofold symmetry is maintained by copying the deformation using a General Extrusion operator. The resulting design and S-parameters are drawn in the plot below.
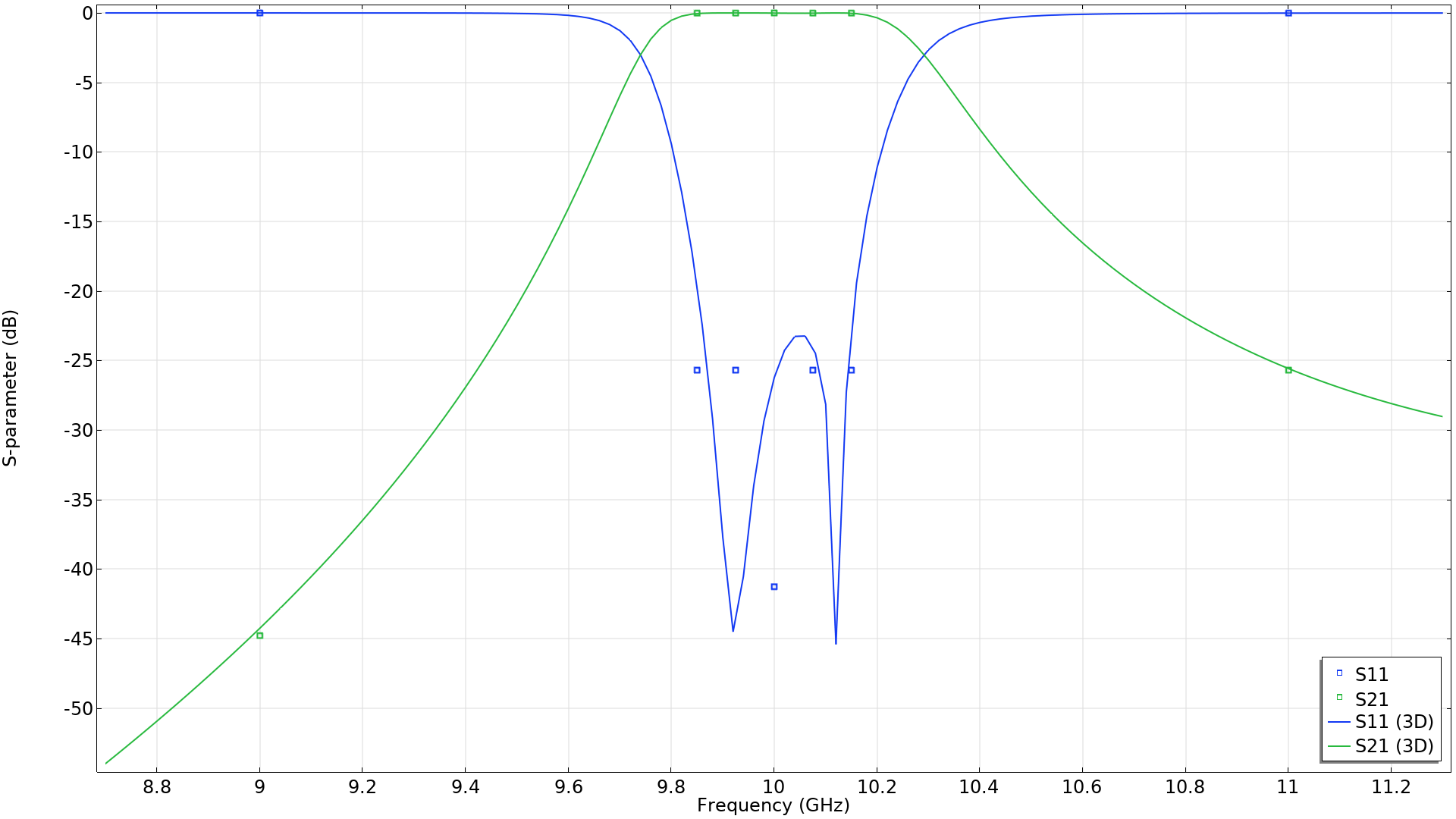
Shape optimization of an RF filter gives the design drawn in black lines (left). The lines in the gray ellipse are optimized, and the shape change is copied to the other lines so that the twofold symmetry is maintained. The corresponding S-parameters are plotted as a function of the frequency in the graph to the right. The points in the graph indicate the frequencies used for optimization.
The optimized design can be extruded so that the performance can be verified in a 3D component, as shown with the lines in the graph above.
One can also design a filter by combining the Polynomial Boundary feature with a different initial geometry as demonstrated in Optimization of a Waveguide Iris Bandpass Filter — Polynomial Version. This has 33 % more control variables and slightly better objective (for the 3D verification), but it also has sharper corners. It’s difficult to predict the best strategy for a particular application beforehand, and one will generally achieve higher performance with more design freedom, but this might be costly later in the design process. It’s thus common that one has to compromise between high performance and cost. COMSOL® makes it easy to set up the same problem in different ways with varying amounts of design freedom, providing users with the data necessary to make an informed decision.
Example 2: Diplexer
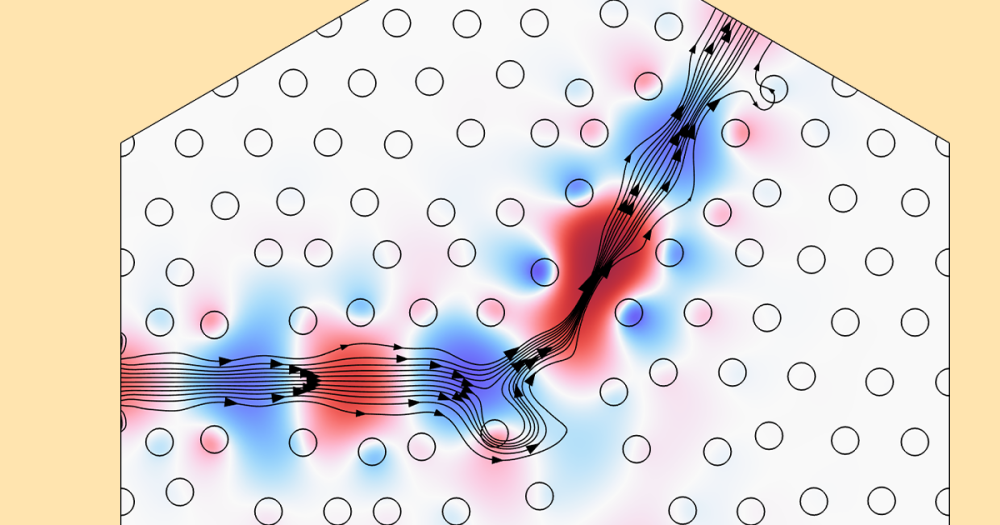
The second example is a diplexer, so the idea is to accept an input signal and route it to different output ports for different frequencies. This is similar to the second example in the first blog post, except here we will use the Polynomial Boundary feature. The coordinates of the vertices in the geometry are optimized, but the lines remain straight since first-order polynomials are used. Also, while the specification of the objective function follows the same ideas as outlined previously, it’s desired that the output spectrum is free of peaks (resonances) in the out-of-band rejection range. Enforcing this requires a somewhat elaborate expression. The formulation of the objective function can be seen in the Designing a Waveguide Diplexer for the 5G Mobile Network using Shape Optimization model. A Symmetry/Roller feature is imposed on the lines adjacent to the input and output ports, so that these lines can change length, but not orientation. The optimization is illustrated in the animation below.
The animation shows the z-component of the electric field for the two pass frequencies during the optimization. It also shows the relevant S-parameters.
The frequencies used for optimization are drawn as points in the graph below, while the lines represent a frequency sweep with a much finer resolution based on a mesh generated in the deformed configuration.
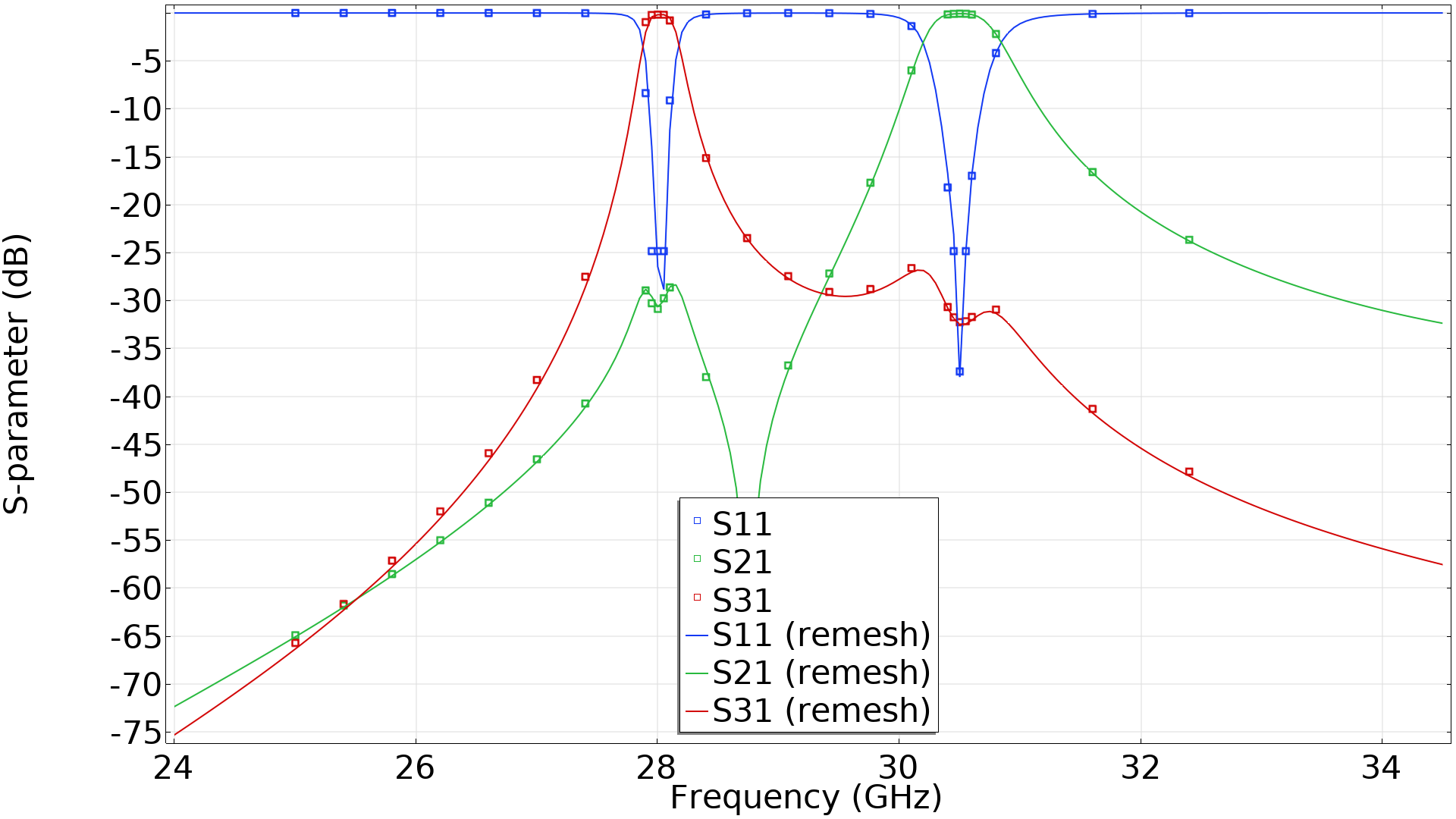
The graph shows the S-parameters for the optimized design as a function of the frequency. The lines are computed after remeshing in the deformed configuration.
As indicated with the points in the graph above, the problem calls for the evaluation of 26 frequencies, but two objective functions are used for every frequency — so evaluating the sensitivity requires solving 52 linear problems. The problem is embarrassingly parallel, and the graph below demonstrates how the computational time can be reduced by using cluster functionality.
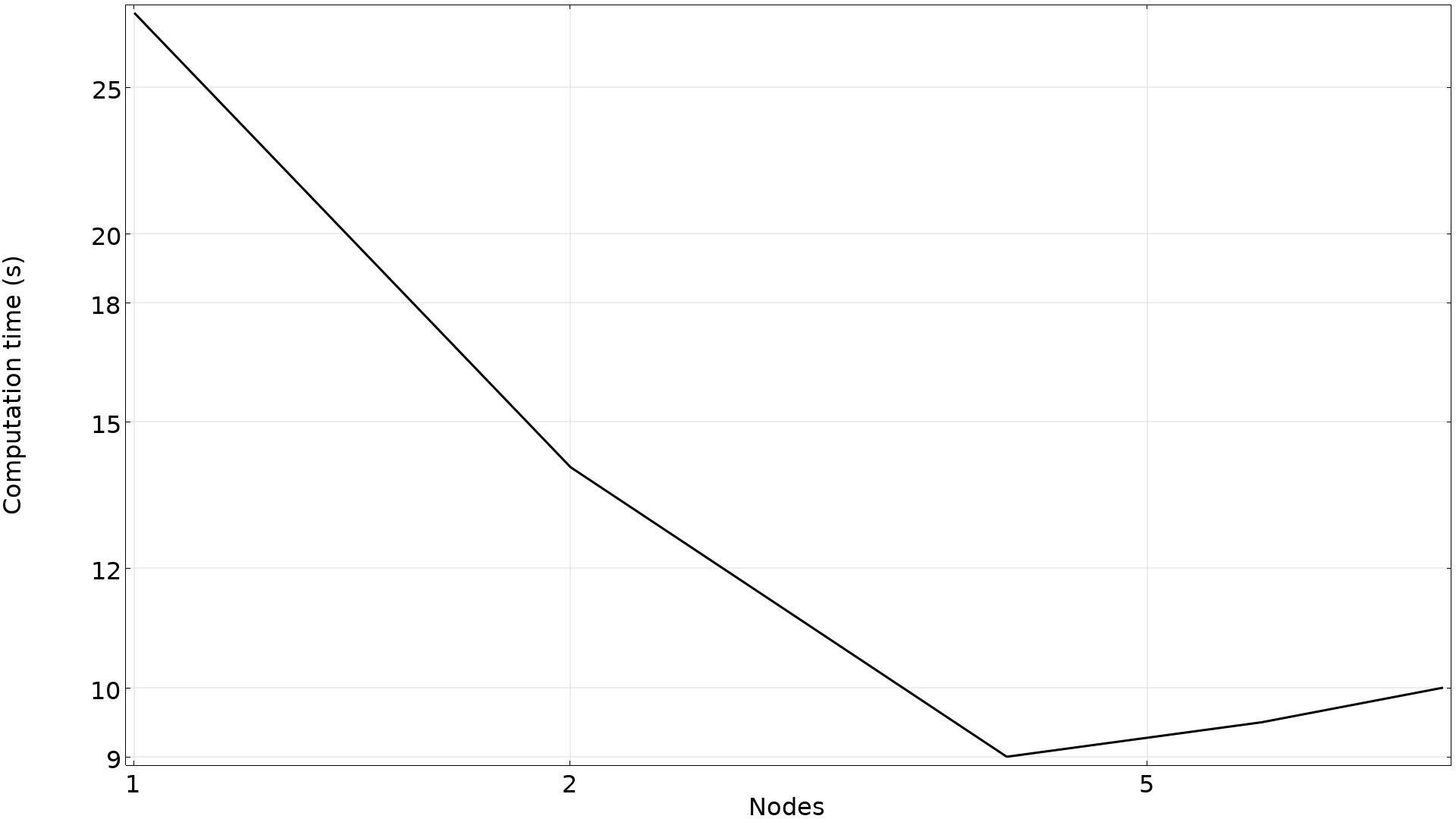
The computational time for a single optimization iteration is illustrated for 1, 2, 4, and 8 nodes on a cluster. Good scaling is observed with 4 nodes even though the model only has 8.5 k degrees of freedom. But, beyond this point, the added cost of communication exceeds the savings in computational time, so the total computational time actually increases.
The good scaling means that it’s possible to solve the optimization problem in under 30 minutes with the use of 6 nodes.
Final Thoughts
In this blog series we have discussed the benefits of performing shape optimization and have shown several examples within electromagnetics. Note that while this series focused on shape optimization in two dimensions, it’s also possible to perform shape optimization for 3D wave propagation problems.
Next Steps
Interested in working with other tutorial models that focus on shape optimization? Here are our suggestions:
- To see how to design a filter with triangular irises using the Polynomial Boundary feature, download the Optimization of a Waveguide Iris Bandpass Filter — Polynomial Version model.
- If you are interested in maintaining a certain wall thickness in your model using a General Extrusion operator and/or stopping optimization once a certain criteria has been met, check out the Shape Optimization of a Water Heater model.
- To see an example of performing shape optimization for 3D wave propagation problems, download the Shape Optimization of a Rectangular Loudspeaker Horn in 3D model.



Comments (0)