
The Van Allen radiation belts consist of highly energetic charged particles that have become trapped in Earth’s magnetic field. These particles follow the shape of the field and give the belts a donut-like appearance. To study the behavior of the particles in the Van Allen belts, scientists can use the Particle Tracing Module, an add-on product to the COMSOL Multiphysics® software.
What Are the Van Allen Belts?
The Van Allen belts, named after James Van Allen, are two donut-shaped belts of radiation that surround Earth. Extending outward from about 1000 to 60,000 km, these belts fluctuate in size, sometimes expanding and shrinking in large orders of magnitude over the course of a couple of hours.
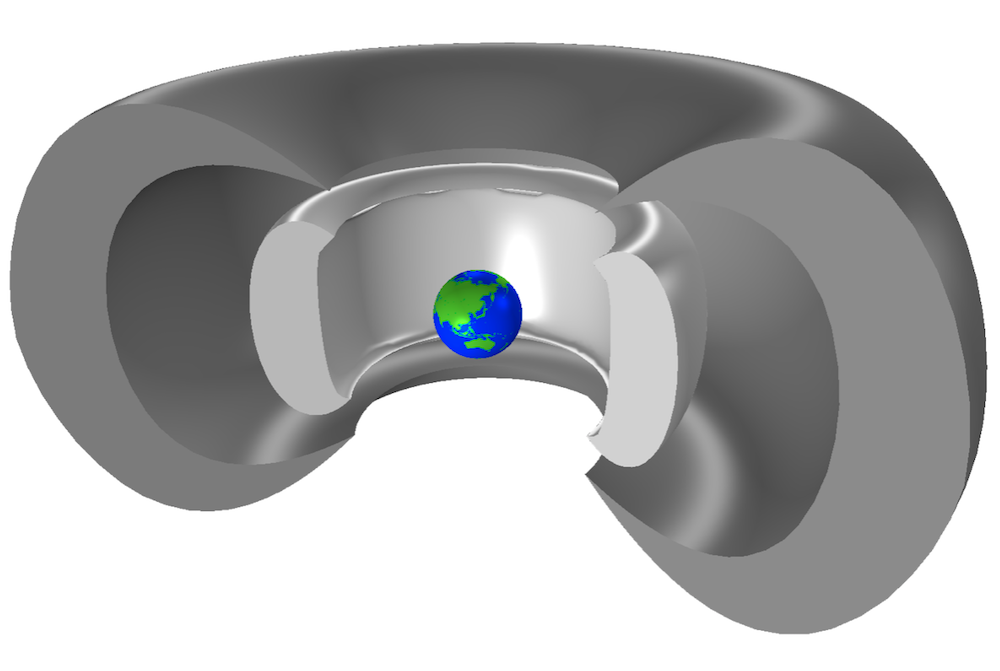
The inner (light gray) and outer (dark gray) Van Allen belts around Earth. The projection of Earth’s landmass is based on images by M.J. Brodzik and K.W. Knowles (Ref. 1).
While research into what affects the shape and size of these belts is still ongoing, scientists have made significant breakthroughs over the years. In 2012, NASA launched the Van Allen Probes, which showed just how complex the belts are. Much to the researchers’ surprise, the probes detected a temporary third belt (caused by a solar storm), which disappeared within a few weeks. The team also learned that only some of the particles within the belts affect the shape, while others are present at all times.
Due to the complexity of the belts, it’s important to clearly understand the fundamental physics. With particle tracing simulation, it’s simple to study the movement of particles trapped in Earth’s magnetic field and see how they give the belts their distinctive shape.
The Motion of Particles in Earth’s Magnetic Field
Earth’s magnetic field is extensive, surrounding the planet for thousands of kilometers. The field is similar to a dipole, although there are certain asymmetries and irregularities. Because the magnetic field is responsible for trapping the particles and they follow its shape, it’s important for scientists to have an accurate model of the field. The standard is, of course, the International Geomagnetic Reference Field (IGRF), which is regularly updated based on the latest findings.
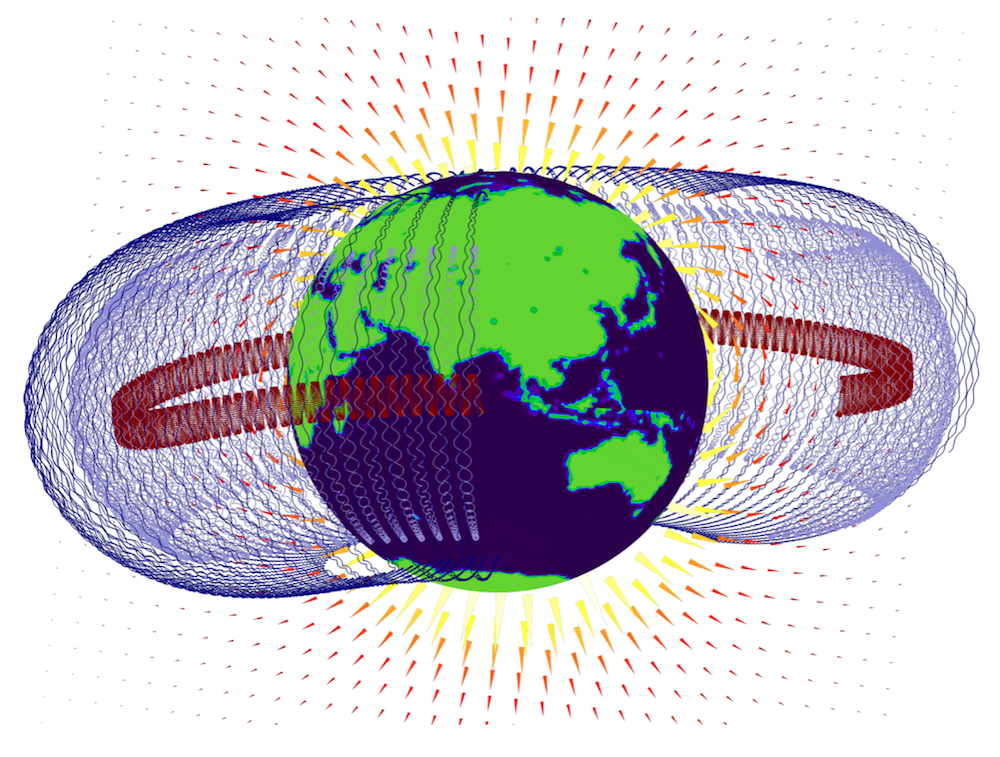
Simulation of the Van Allen belts around Earth. The projection of Earth’s landmass is taken from images in Ref. 1. (Note that this image was created by running the model discussed below for a longer time interval.)
When particles enter this field, they begin to spiral around a field line toward one of the poles. As they approach, their pitch angle (i.e., the angle between the direction of the magnetic field and a particle’s trajectory) increases due to the increasing magnitude of the magnetic field, leading to the dip in the donut’s center. With the higher angle, eventually, the particle reaches a point (known as the mirror point) where it bounces, heading toward the other hemisphere. If the particle doesn’t become lost to the atmosphere, the pattern continues and the particle drifts from one field line to the next, gradually making its way around Earth.
Simulating the Motion of Particles Using the IGRF Model
This 3D example examines the path that particles, specifically protons, take while trapped in Earth’s magnetic field. The model consists of a simple sphere of radius Re, which represents Earth, and a larger spherical simulation domain of radius 5Re, where the particle trajectories are computed.

The magnetic field domain around Earth. Note that in the model, Earth is represented by a simple sphere. Here, the projection of Earth’s landmass is taken from images in Ref. 1.
To quickly compute the magnetic fields, it’s possible to use an external function to incorporate the data from IGRF into a simulation. Accessing this data is simple using the built-in Earth’s magnetic field option in the Magnetic Force feature, available in both the Charged Particle Tracing interface and Particle Tracing for Fluid Flow interface. Here, the Charged Particle Tracing interface is used with a time-dependent study.
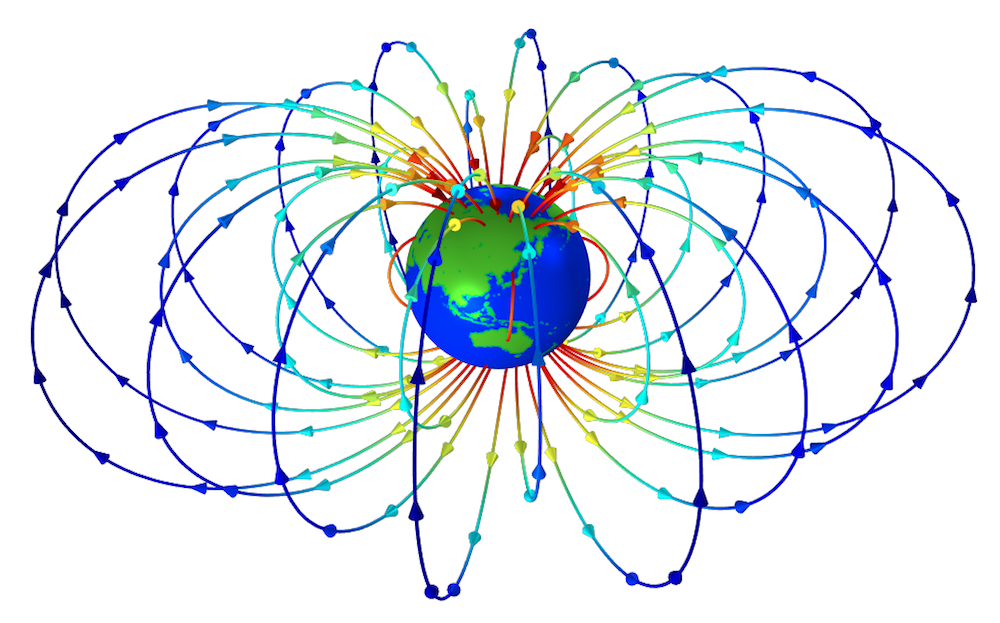
The magnetic field lines are based on data from IGRF, while Earth’s landmass is based on images in Ref. 1.
Another feature, named Release from Grid, makes it easy to model the release of protons at a particular equatorial pitch angle. In this model, the equatorial pitch angle of the 10-MeV proton is set to 30°.
Examining the Results of the Particle Tracing Simulation
The simulation shows the three components of the proton’s motion:
- Gyration
- Bounce
- Drift
While not displayed below, the timescales for drift motion are much longer than those for bounce motion, which are in turn much longer than the gyration period.
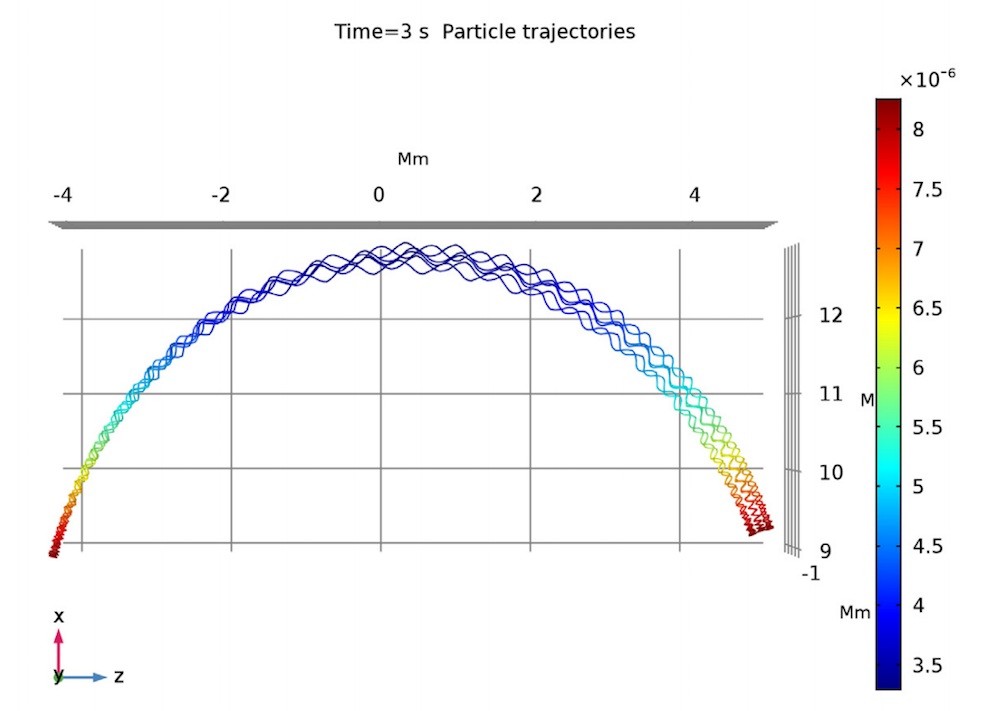
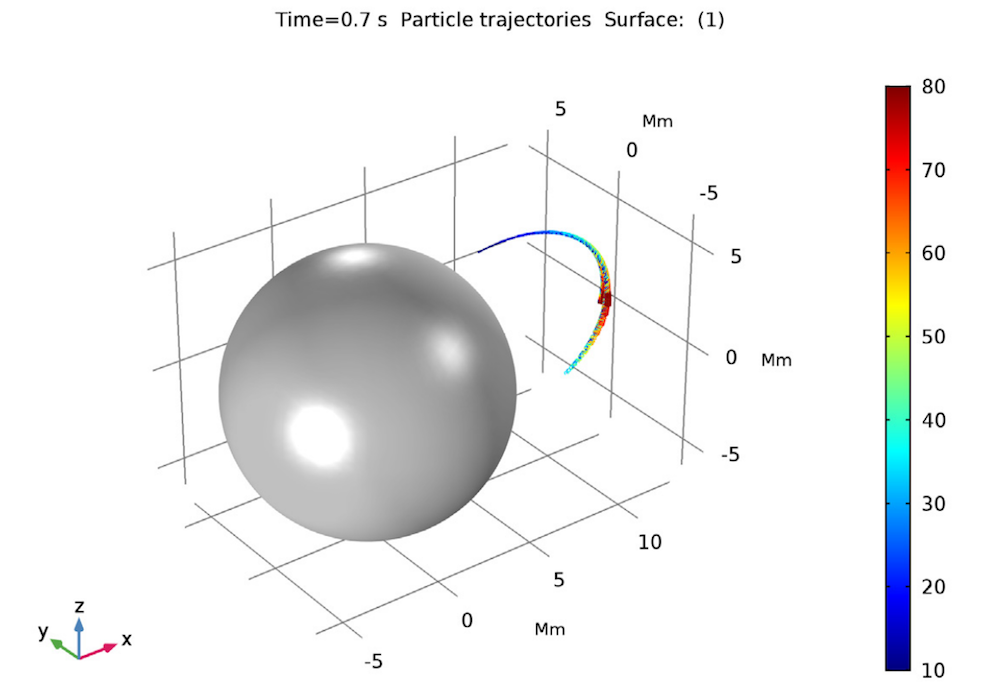
The trajectory of a proton in Earth’s magnetic field.
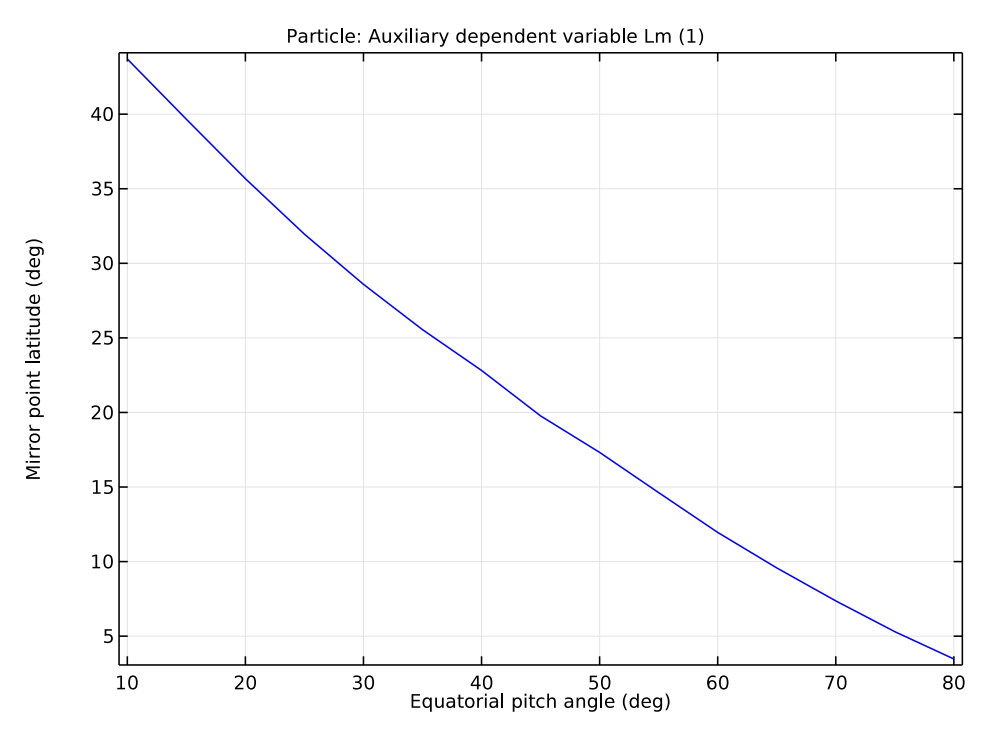
Scientists can also use models like this one to look at the effect of various equatorial pitch angles on the mirror point latitude. As expected, the mirror point latitude increases as the pitch angle of the particle decreases. At the limits of the plot, a particle with an equatorial pitch angle of 90° remains in the equatorial plane, whereas a particle with a pitch angle of 0° travels directly along the field line without bouncing. If there’s no bounce, the particle falls down toward Earth to form an aurora.
Left: The trajectories of multiple trapped protons, with the color expression corresponding with different equatorial pitch angles. Right: Mirror point latitude against the equatorial pitch angle for a particle.
To better visualize the results, you can create an animation. The one below depicts the movement of a trapped proton, showing how the particle’s pitch angle increases near the poles. You can also see the beginnings of how the particle’s movement creates the belts’ signature donut-like shape.
Animation of a trapped proton in the Van Allen belts. The projection of Earth’s landmass is based on images in Ref. 1.
With particle tracing simulation, scientists can gain a better understanding of the behavior of particles in the Van Allen belts, important information for more complex studies in the future.
Next Steps
If you want to try modeling the motion of protons within Earth’s magnetic field, click the button below. Doing so will take you to the Application Gallery, where you can log into your COMSOL Access account and then get the tutorial documentation and MPH-file.
Additional Resources
- Read more about particle tracing simulation in the Phase Space Distributions in Beam Physics blog series
- Learn how to add custom particle-particle interaction forces in the Rotating Galaxy tutorial
References
- Brodzik, M. J. and K. W. Knowles. 2002. EASE-Grid: A Versatile Set of Equal-Area Projections and Grids in M. Goodchild (Ed.) Discrete Global Grids. Santa Barbara, California USA: National Center for Geographic Information & Analysis.





Comments (0)