
In a recent video on the Stand-up Maths Youtube channel, the problem of the hopping hoop is discussed. Despite its apparent simplicity, the physics and mathematics of this problem has attracted interest from a number of researchers over the last half-century. In this blog post, we present a few models that can provide physical insight into what is really going on.
The Problem
The original problem statement is: An ideal, massless, rigid ring has a single point mass attached to its perimeter. If the ring is rolled along a horizontal plane, is it possible that it will disconnect from that plane and hop up into the air? The motion starts with the ring in the unstable equilibrium position where the mass is at its highest point.
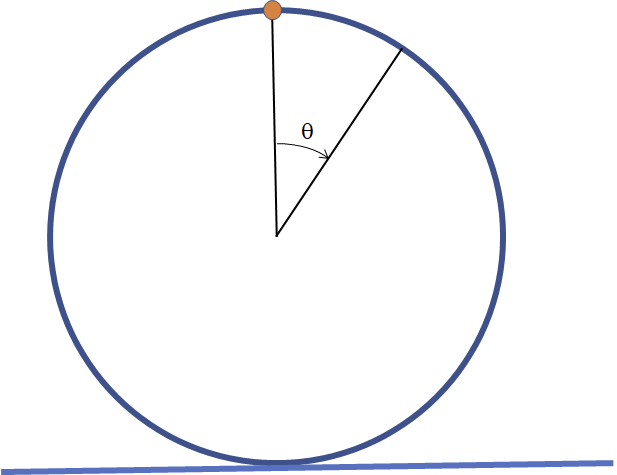
In this blog post, we will look at a ring that is similar to one that is discussed in the video, with some slight modifications. For instance, the ring is no longer massless, but has a uniformly distributed mass. The total mass of the system is m, where \gamma m is the fraction of the mass assigned to the point mass, and the rest of the total mass, (1-\gamma)m, is distributed around the ring. Using the special case \gamma = 1, the original configuration is then recovered. The exact physical properties are not important here, but can be used for reference: The ring radius is R = 1 \ m, the total mass is m = 1 \ \text{kg}, and the mass distribution parameter is \gamma = 3/4. The coefficient of friction between the ring and the plane is set to \mu = 1.
There are a few different places in the geometry where the velocity can be measured. Unless anything else is stated, velocity (v) means the velocity of the ring center. During pure rolling motion, it’s related to the angular velocity through v = R \dot \theta.
A First Attempt
To become better acquainted with the problem, we will start by rolling the ring at a low speed. The ring is simulated using a rigid body in the Multibody Dynamics interface. The Rigid Body Contact feature is used to simulate the connection between the ring and the plane.
The reference configuration (at zero rotation) is when the point mass is located at the top of the ring. If we give the ring just the smallest push (in this case, an initial velocity of {v}_{\textsl 0} = 0.1 \ m/s), the rotation will have a very slow start, but as the vertical position of the point mass drops, the speed increases. The rotational speed varies substantially during one revolution, and as the point mass reaches the top again, the ring has almost reached a standstill. This is shown in the animation below.
The ring is colored by velocity. The black trace shows the path of the point mass (a cycloid). The green trace shows the path of the center of gravity of the system. The arrows are proportional to the contact forces.
Let’s investigate some key features in more detail. First, we plot the velocities. The angular velocity is multiplied by the hoop radius so that it can be directly compared with the translational velocity at the center. As long as the motion is a pure rotation, the curves will coincide.
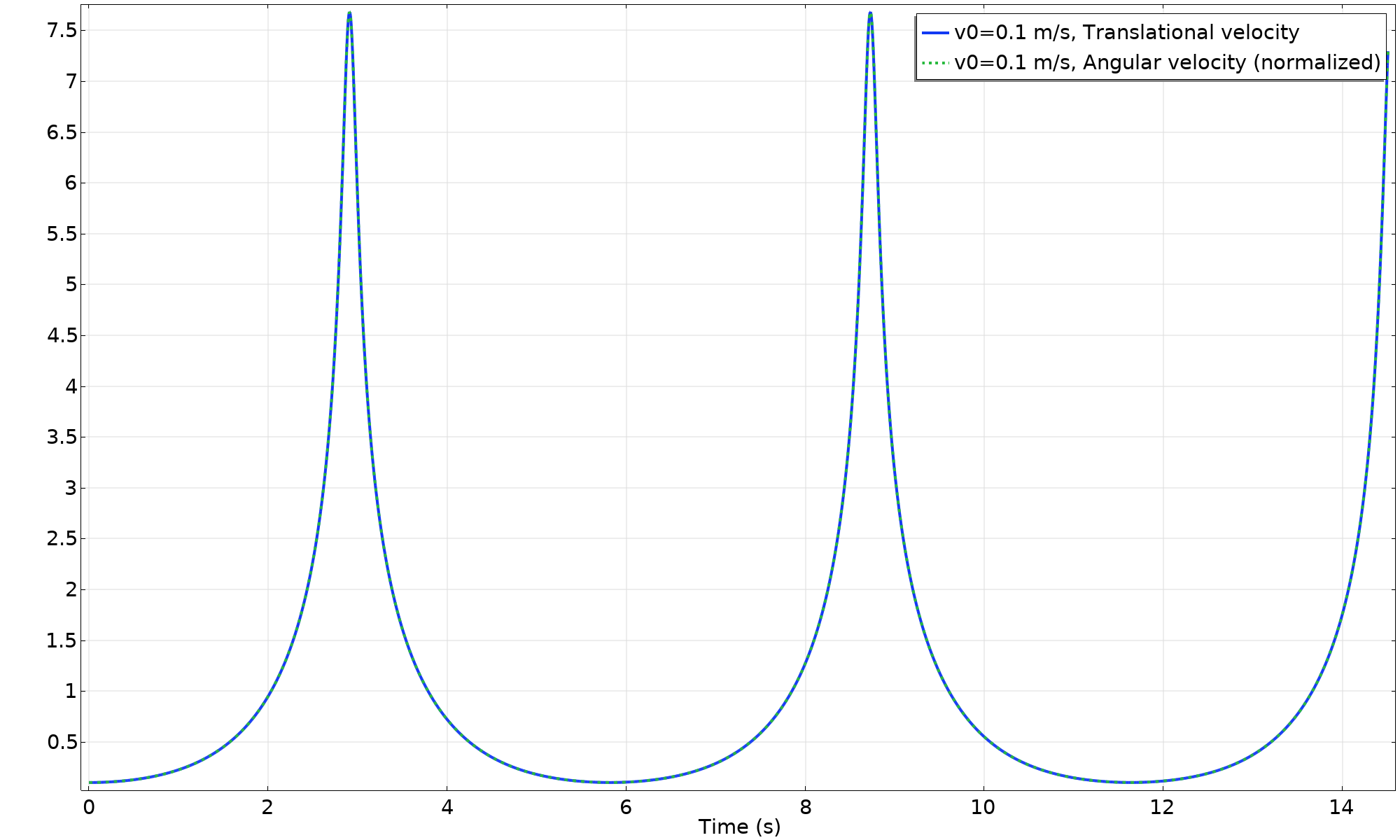
The velocity plotted versus time.
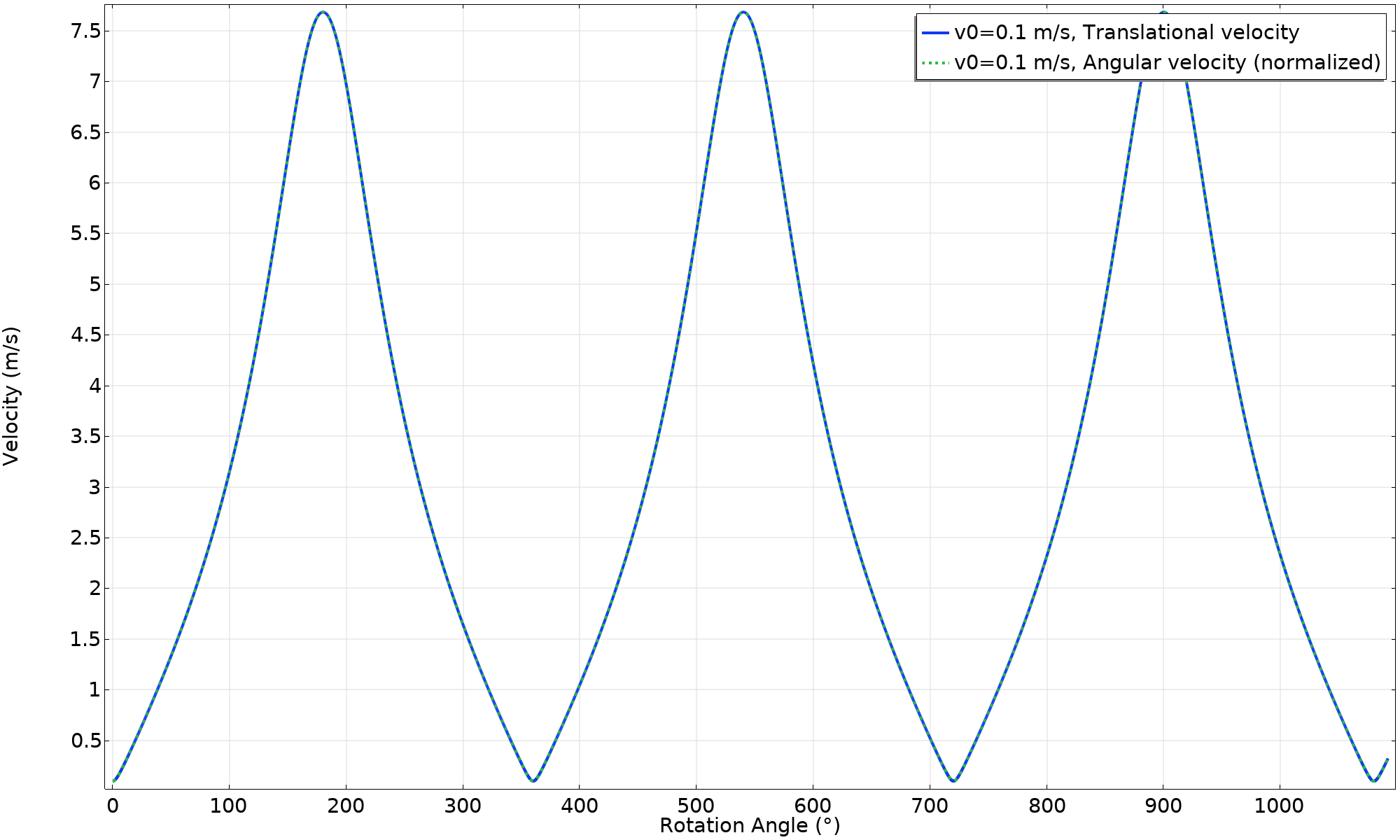
The velocity plotted versus rotation angle.
The potential energy of the point mass can be considered as the driving force for the rotation. The mass of the ring itself does not change altitude unless the ring happens to hop, so that fraction of the mass does not contribute to potential energy if the ring is simply rolling.
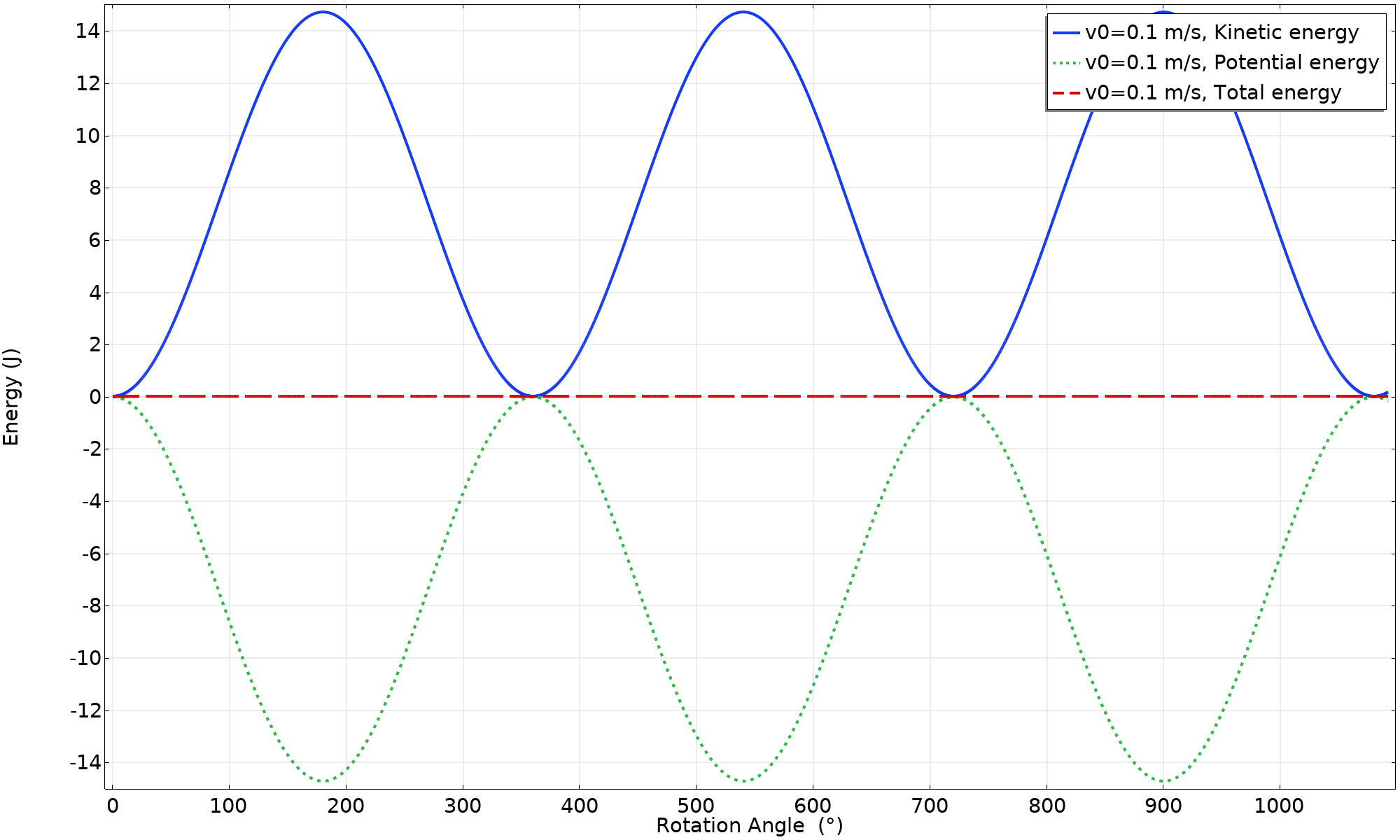
The potential and kinetic energies of the system.
When plotted against the angle, the energy conversion varies as a pure harmonic function. This is a direct consequence of the vertical position of the point mass.
We will make a short digression into the theory, with a fun twist at the end.
The potential energy of the system is only affected by the vertical position of the point mass, and can be written as:
The reference height is selected so that the potential energy is zero when the point mass reaches its top position.
The kinetic energy can, after some algebra that includes the location and velocity of the center of gravity, be written as:
Given the expressions for both types of energy, the principle of energy conservation can be used to arrive at a closed-form expression for the angular velocity as a function of the rotational angle:
Inserting the expressions for the kinetic and potential energy, we get:
The angular velocity as function of the angle is thus:
The maximum angular velocity must occur at \theta = \pi, and is then:
Note what happens as \gamma approaches 1 (the original problem with only a point mass). The maximum angular velocity approaches infinity! This sounds alarmingly unphysical.
The problem is that in a rolling motion, the contact point between the ring and the floor is always at rest. When all the mass is located there, the kinetic energy is thus zero. At the same time, the kinetic energy should equal the potential energy lost. This does not sum up! Also, as the original author of this problem (John Littlewood, in his book A Mathematicians Miscellany) states, there should be a hopping motion already when reaching \theta = 90°.
Anyway, this will not happen in reality. To obtain a high velocity, very large accelerations are needed. As a consequence, there will, sooner or later, be sliding for any finite value of the coefficient of friction.
Finally, let’s take a look at the contact forces.
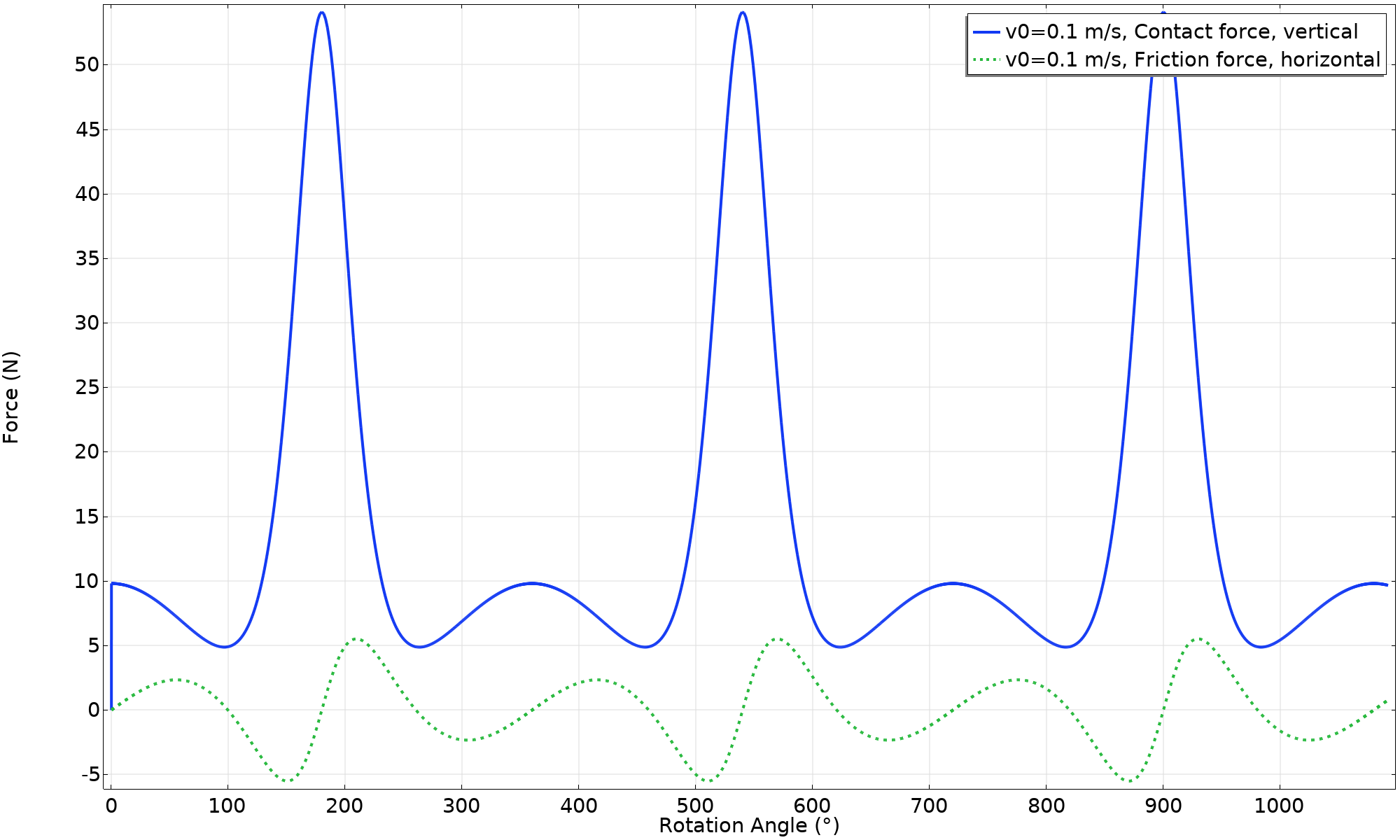
Contact forces acting on the ring.
The horizontal force, caused by friction, is what drives the acceleration and deceleration of the ring. In order to have the pure rolling motion predicted by this animation, there are two requirements:
- The vertical contact force must always be positive (F_{\text n} > 0). If F_{\text n} = 0, the ring has lost contact with the surface.
- The horizontal friction force cannot exceed what is allowed by Coulomb’s friction law (|F_{\text f}| < μ F \text {n}). If this happens, there will be slipping.
An easy check of the friction criterion is to plot the quantity F_{\text f} / μ F \text {n}. In this case, the margin is wide; only about 38% of the available friction force is utilized. Another way of viewing this is that a friction coefficient of at least 0.38 is necessary for maintaining a pure rolling motion.
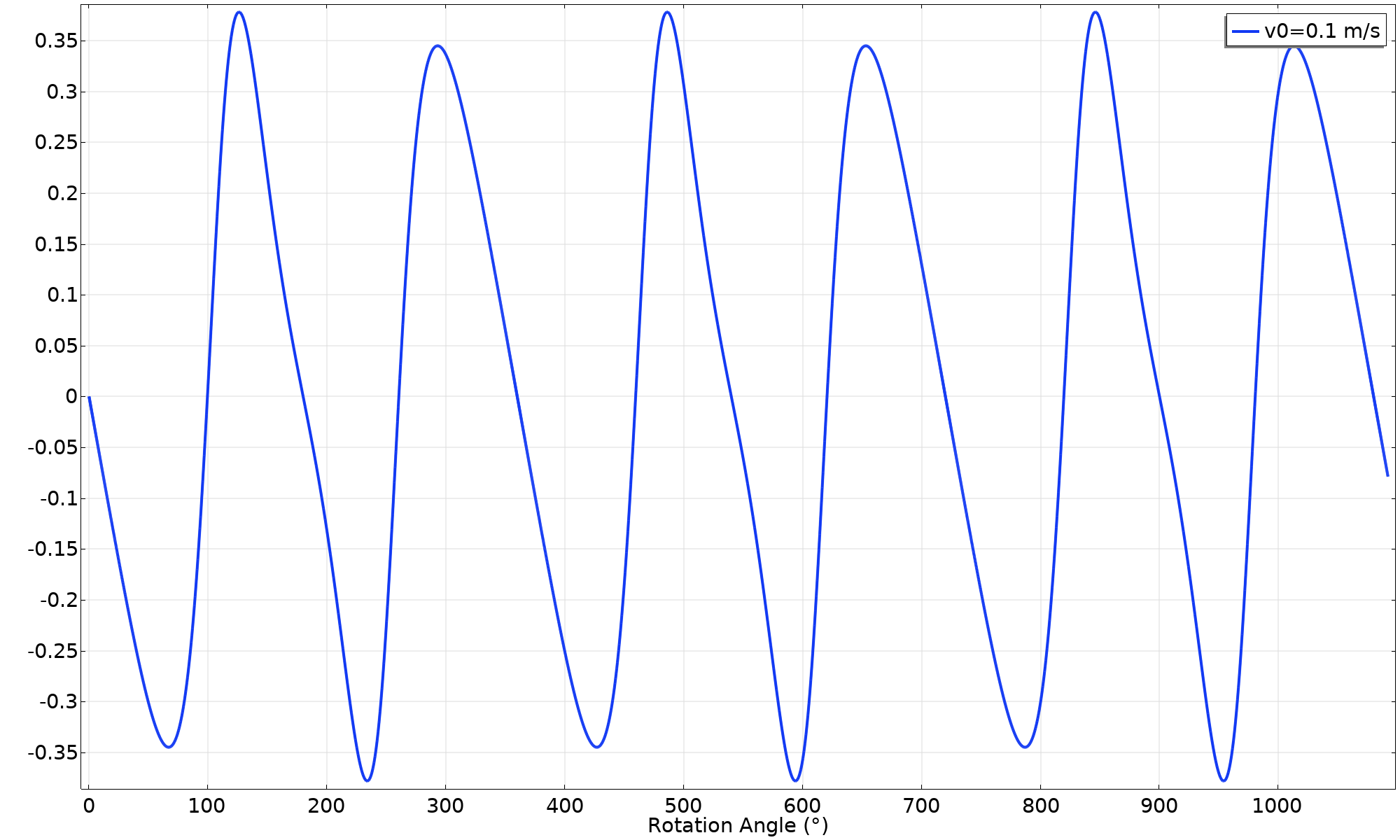
Friction force utilization factor.
Increase the Speed
In the next attempt, a higher initial velocity (v_ \textsl {0} = 2 \ \text {m/s}) is given to the ring. As seen below, there is still a pure rolling motion. However, there are some interesting changes in the results, such as:
- The velocity is higher, but more uniform.
- The minimum contact force has decreased. The reason for this is that with a higher rotational speed, the centrifugal force on the point mass increases. Therefore, when the combination of location and speed is right, there is a large vertical force, offsetting the self-weight of the ring.
- A much larger fraction of the available friction force is used. This is due to the combination of lower contact force and higher reaction force balancing the inertial forces.
Animation of the motion (v_ \textsl {0} = 2 \ \text {m/s}).
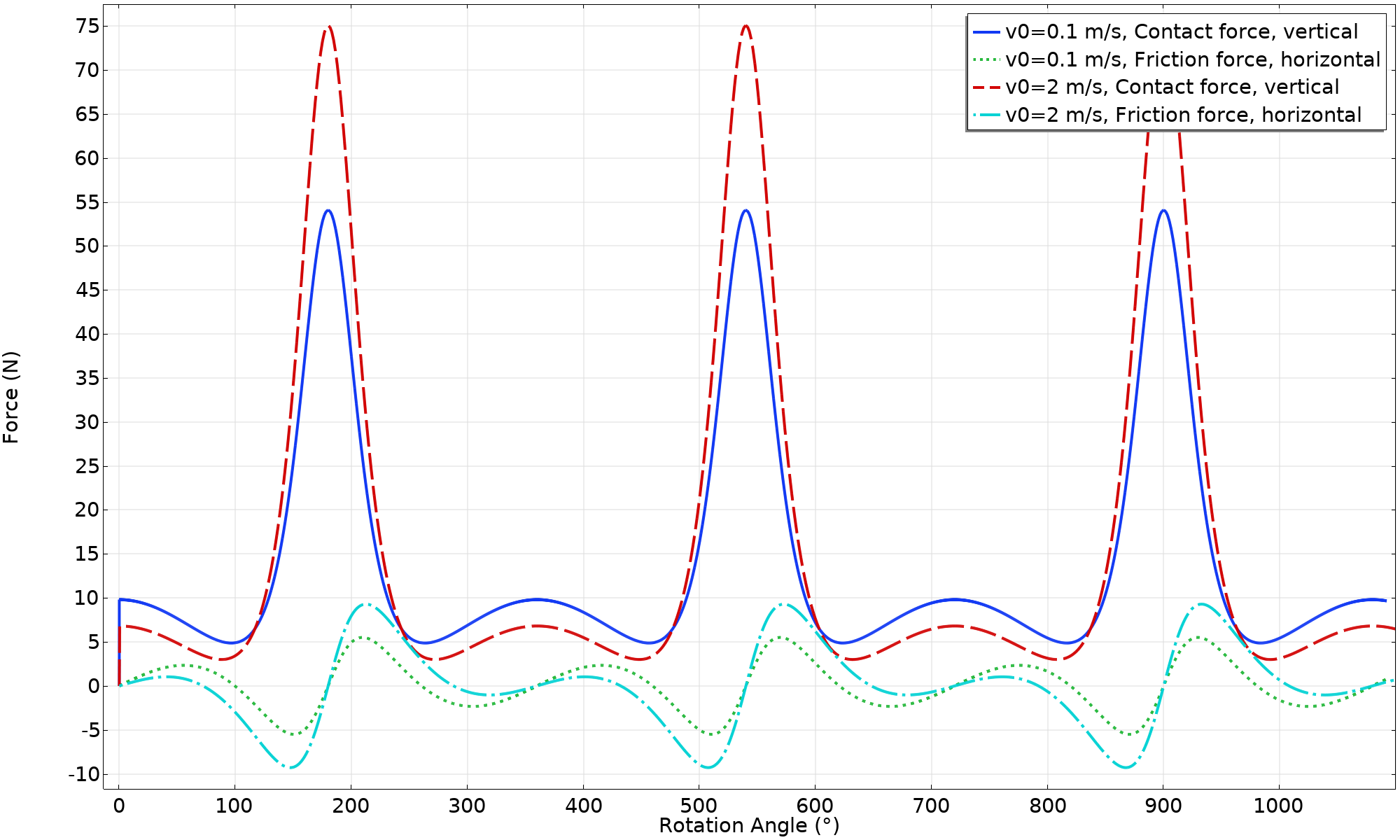
Contact forces acting on the ring (v_ \textsl {0} = 2 \ \text {m/s}).
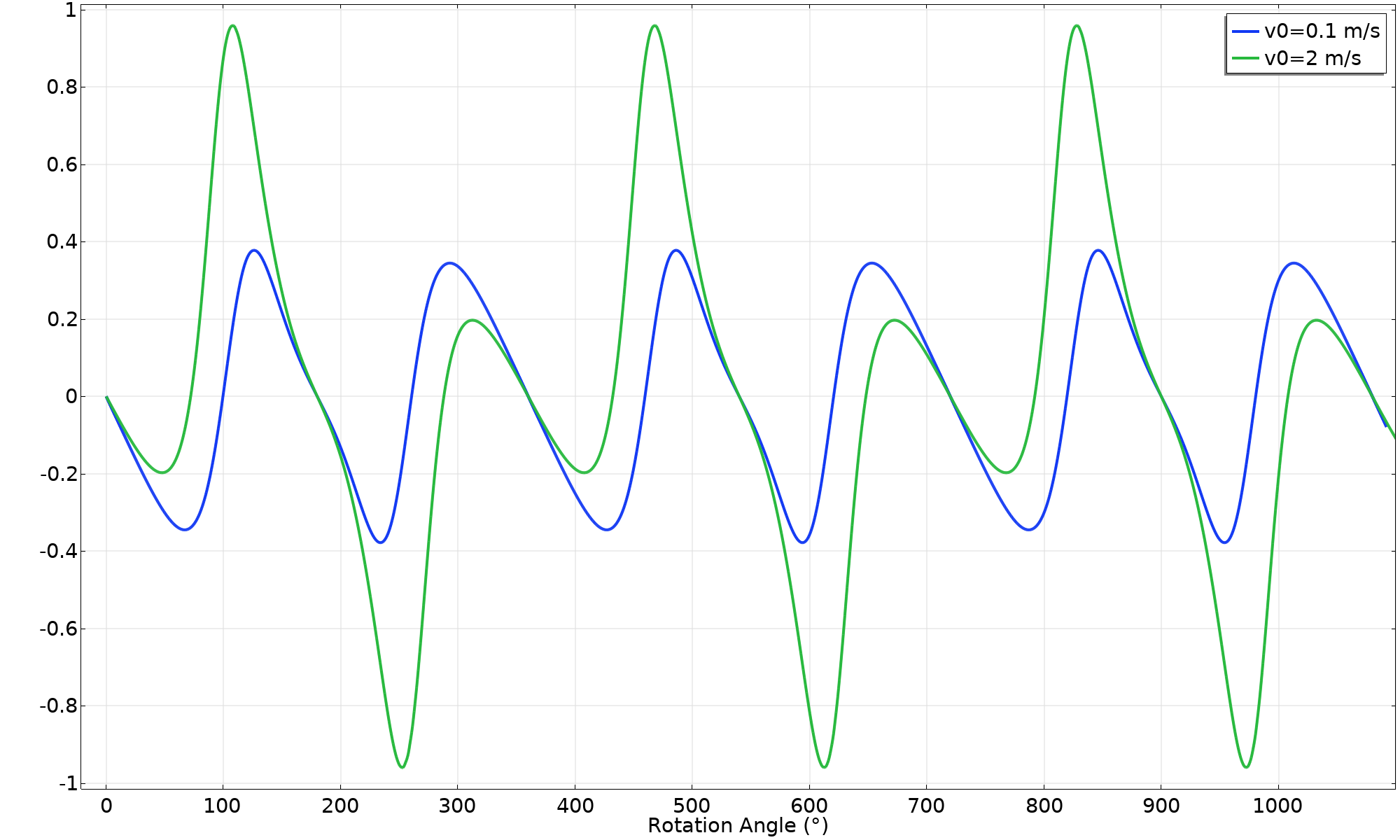
Friction force utilization factor (v_ \textsl {0} = 2 \ \text {m/s}).
If we connect the dots, it’s evident that at some marginally higher initial velocity, slip will occur between the ring and the horizontal surface. In the next attempt, we use v_ \textsl {0} = 2.8 \ \text {m/s}. Now we can see that the friction utilization factor levels out at 1, which means sliding. This is not so easy to determine from an animation, but the velocity plot reveals something: The translational and angular velocities are no longer identical.
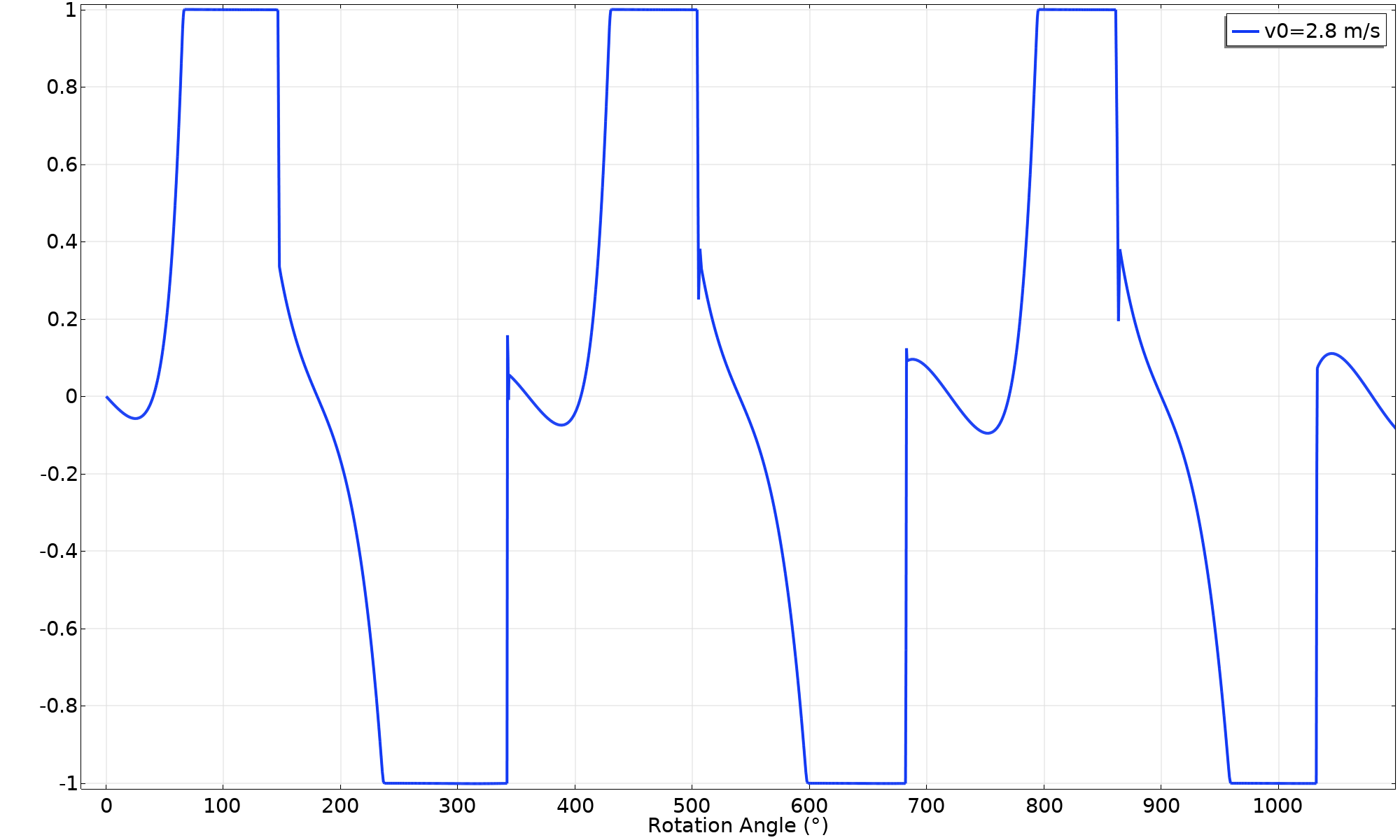
Friction force utilization factor (v_ \textsl {0} = 2.8 \ \text {m/s}).
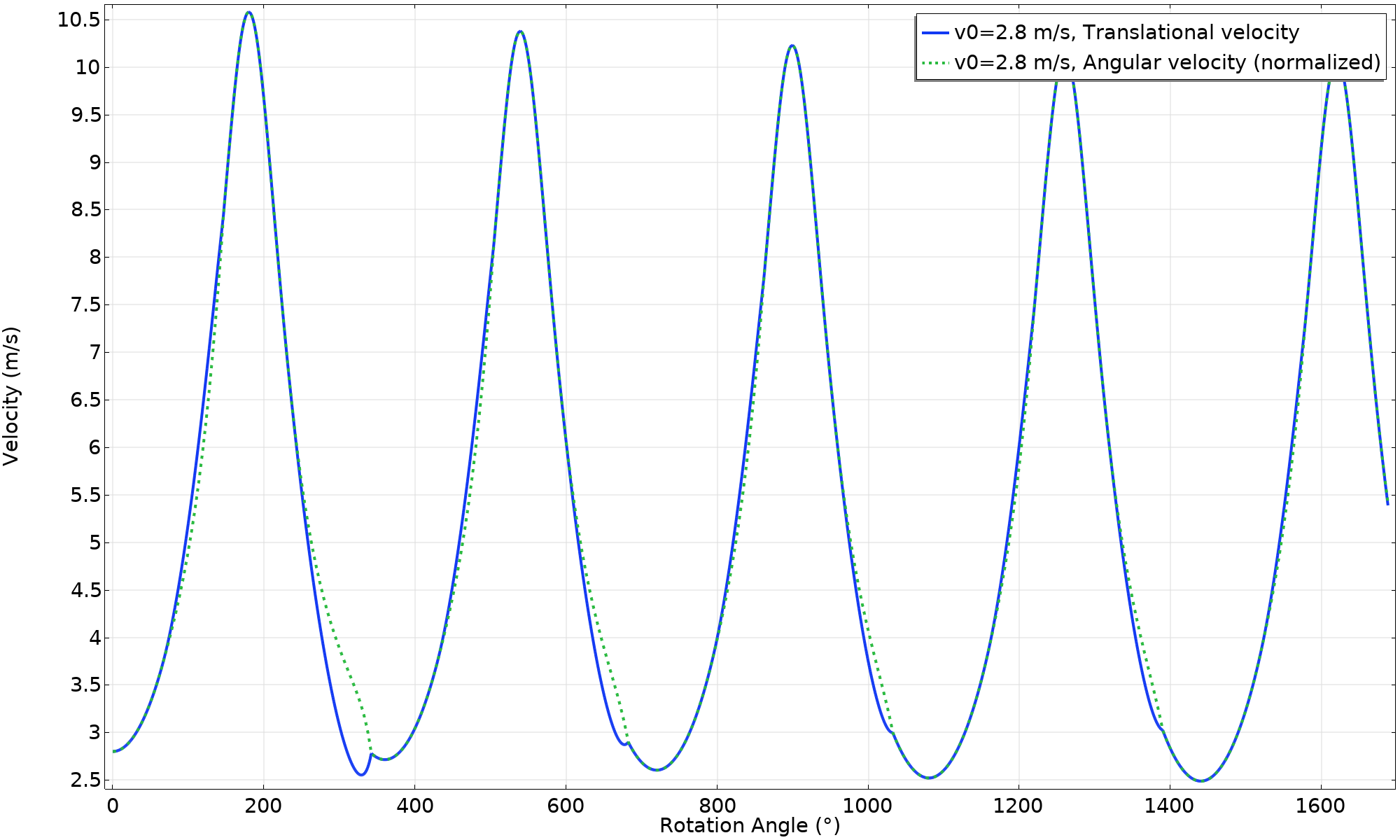
Velocity (v_ \textsl {0} = 2.8 \ \text {m/s}).
As can be seen, the peak value of the velocity is decreasing for each cycle. If we were to continue the simulation, it would end in a pure rolling motion (once enough energy has been dissipated). Below, the energy balance is shown. The “total” energy is defined as the sum of the potential energy and the kinetic energy.
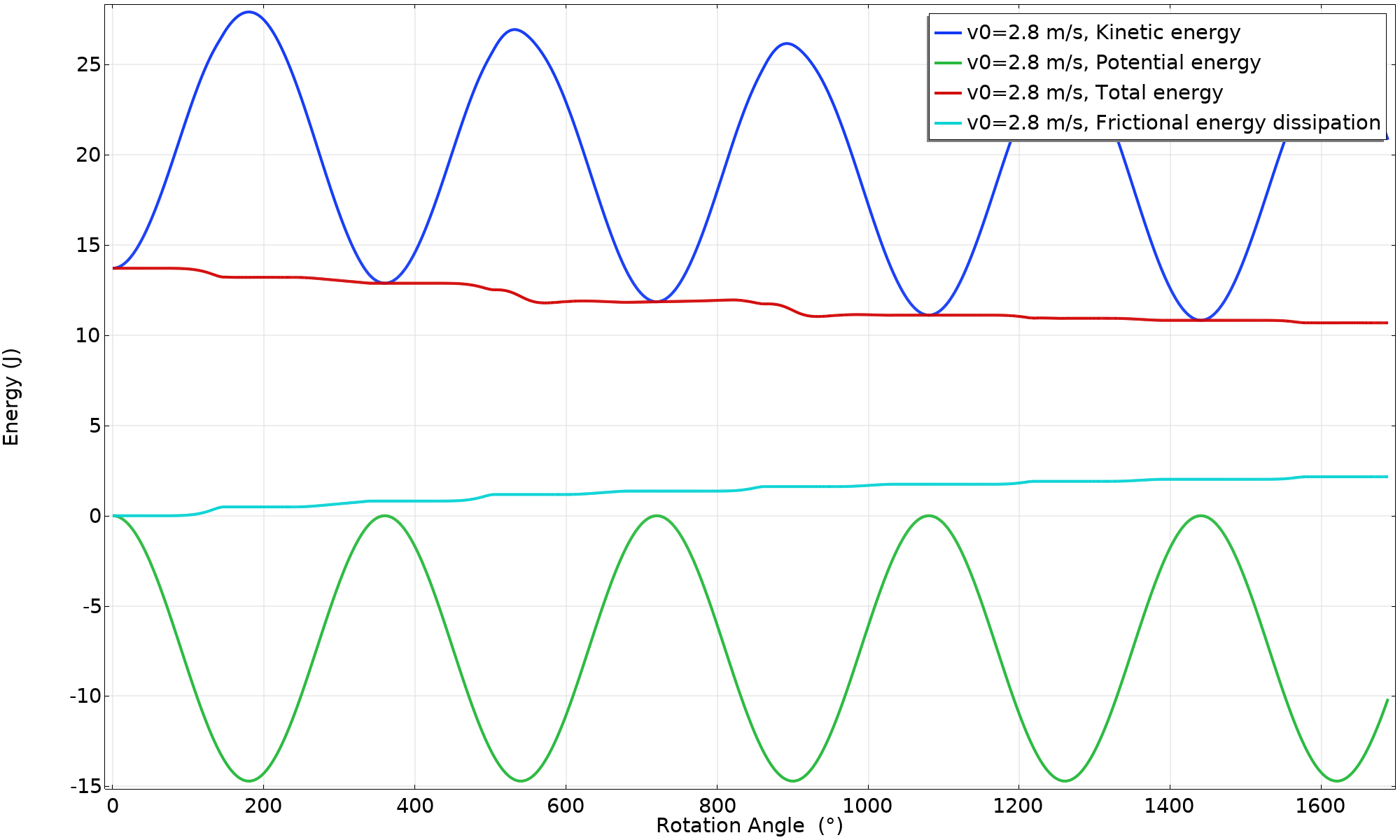
Energy balance (v_ \textsl {0} = 2.8 \ \text {m/s}).
Let’s Hop!
The initial velocity is now increased to 3.1 m/s. This makes the animation really interesting.
Animation of the motion (v_ \textsl {0} = 3.1 \ \text {m/s}).
Note that the jump comes just before a full revolution has been completed. This is, as predicted, at the upper-right corner of the phase diagram shown in the YouTube video. In the plot, the trace for the center of gravity is colored red when the hoop is airborne. That part of the curve forms a projectile motion parabola.
The velocity plot shows that the angular velocity is constant when the hoop is flying. It must be, since no external moment is applied. Less intuitive is that the velocity is not constant, even though there are no forces. Why?
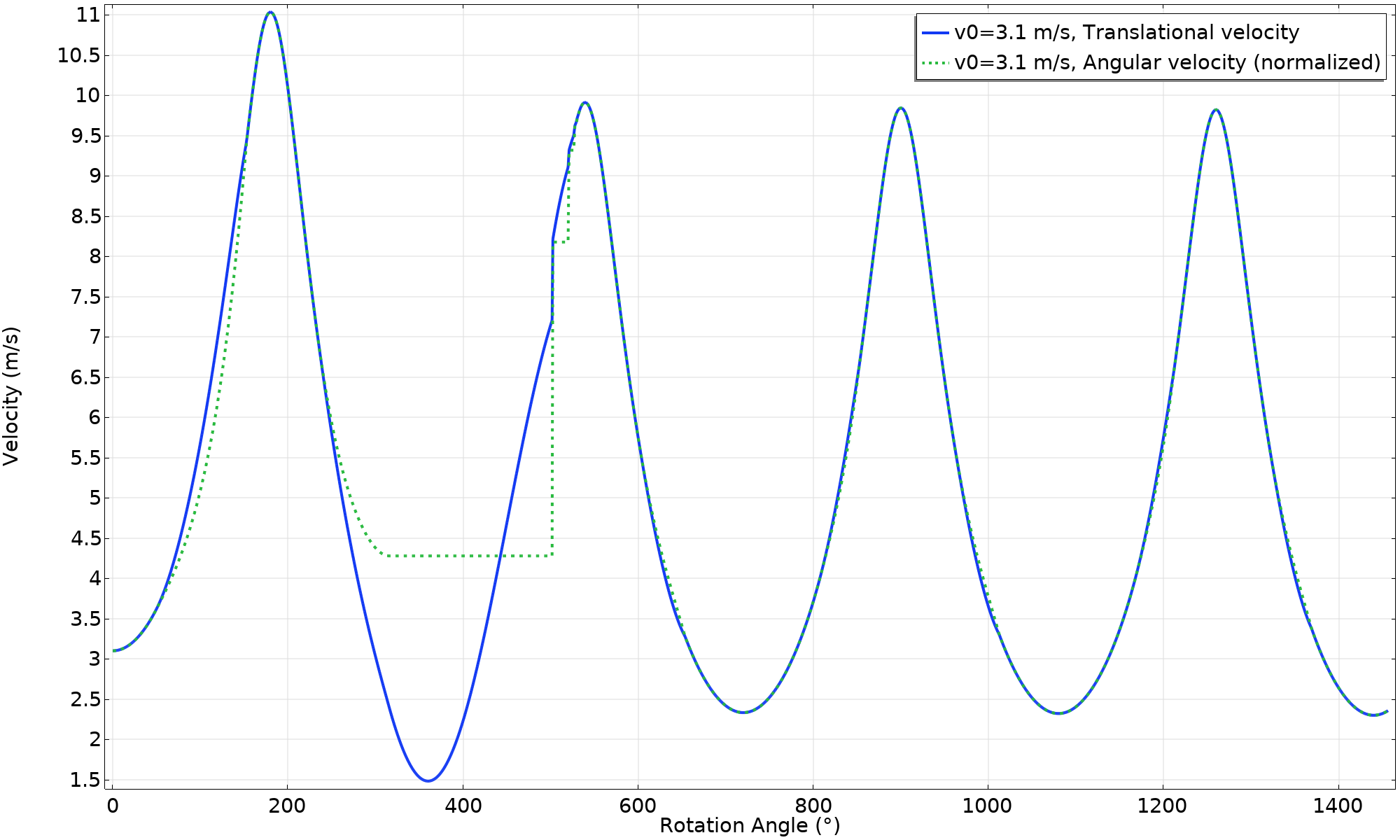
Velocity (v_ \textsl {0} = 3.1 \ \text {m/s}).
Well, the velocity being plotted is that of the center of the ring, whereas it’s the center of gravity that has a constant velocity, The center of gravity actually rotates around the center of the ring.
The energy balance plot gives further insight.
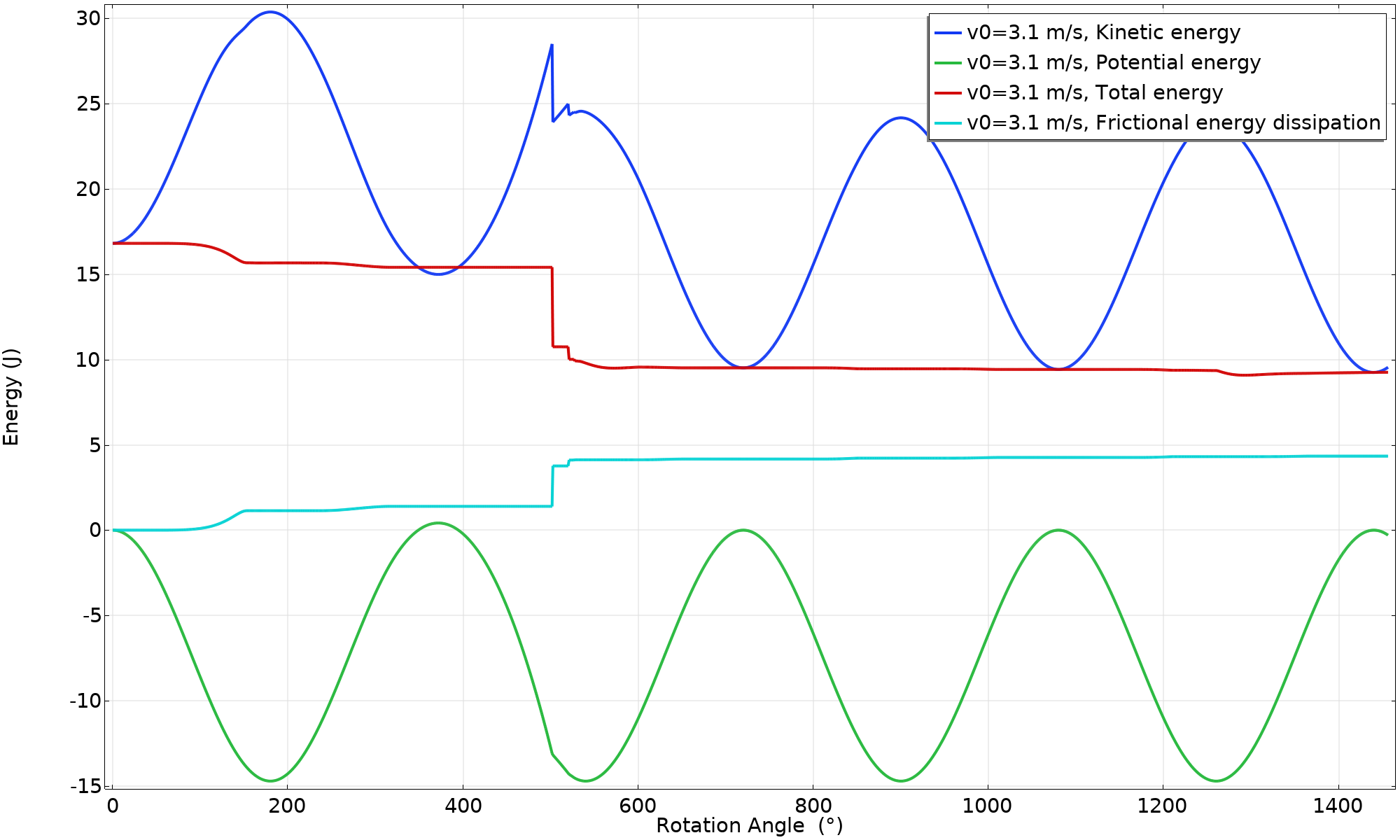
Energy balance (v_ \textsl {0} = 3.1 \ \text {m/s}).
Note that the potential energy is slightly larger than zero during a short period between 350° and 395°, causing the total energy to be larger than the kinetic energy. This is an effect of the center of the ring having moved upward. The expression for the potential energy used in the graphs is based on the actual location, not on the abovementioned expression for W_p, in which rolling is assumed.
In this simulation, there is a pure rolling motion after the landing. This result cannot, however, be trusted. If you look closely, you can see that the energy lost during impact is significantly larger than the frictional losses at the same moment. Both of these loss mechanisms will be closely related to the numerical modeling of the contact condition. We do not have enough data to say something about what should happen during the collision between two rigid objects.
Revisiting Low Friction
We saw in the initial attempt that a friction coefficient lower than approximately \mu = 0.4 would cause sliding, even at very low initial velocity. To check what happens, let’s try it with \mu = 0.3.
Animation of the motion (v_{0} = 0.1 \ m/s, \mu = 0.3).
Since there is sliding, energy is dissipated. There is not enough kinetic energy left in the system to lift the point mass back up to the top position. The wheel starts rolling in the opposite direction, and then rocks back and forth. The lower value of the friction induces sliding several times, as can be seen in the velocity and energy plots. As the movement is not monotonous with respect to the angle, the quantities are plotted versus time, in this case.
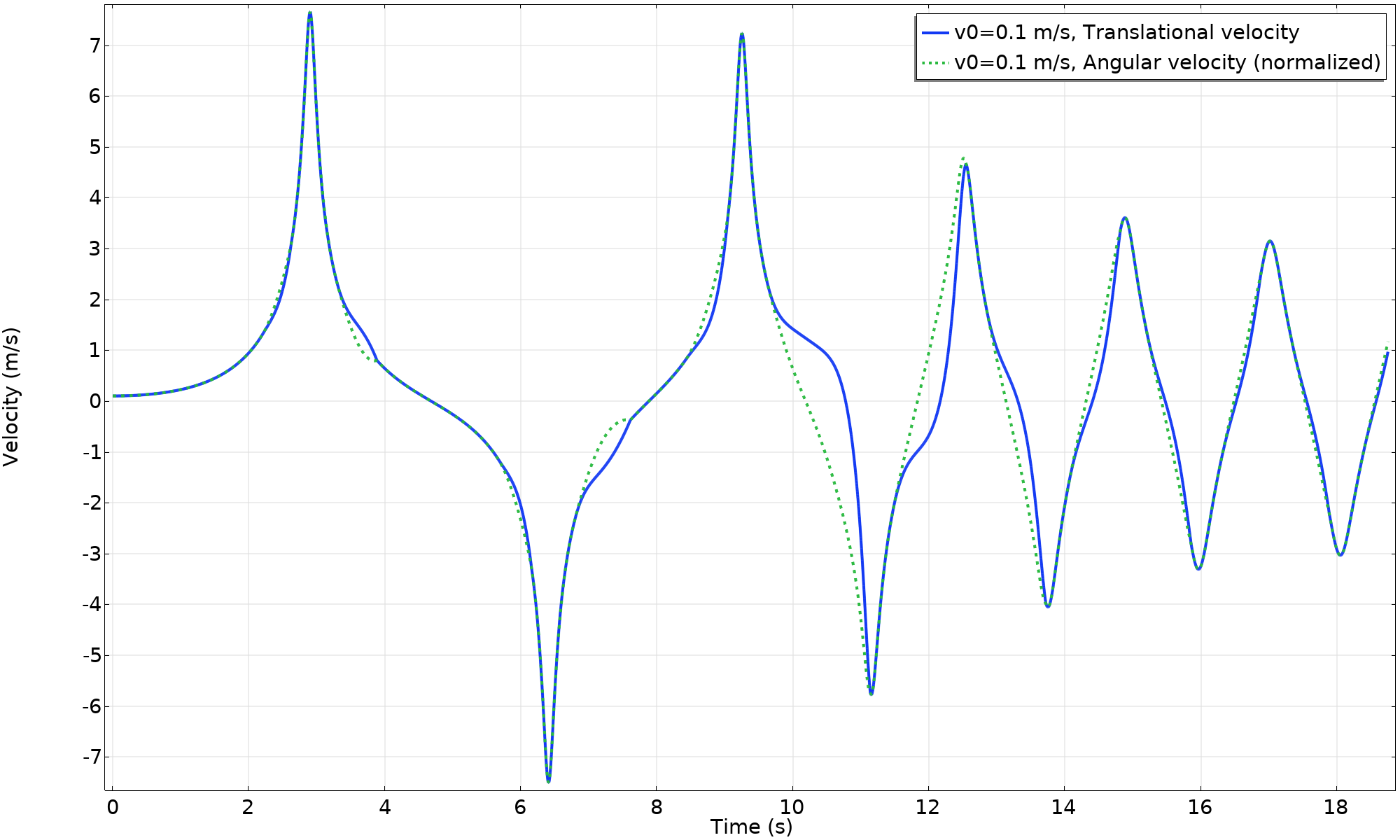
Velocity (v_{0} = 0.1 \ m/s, \mu = 0.3).
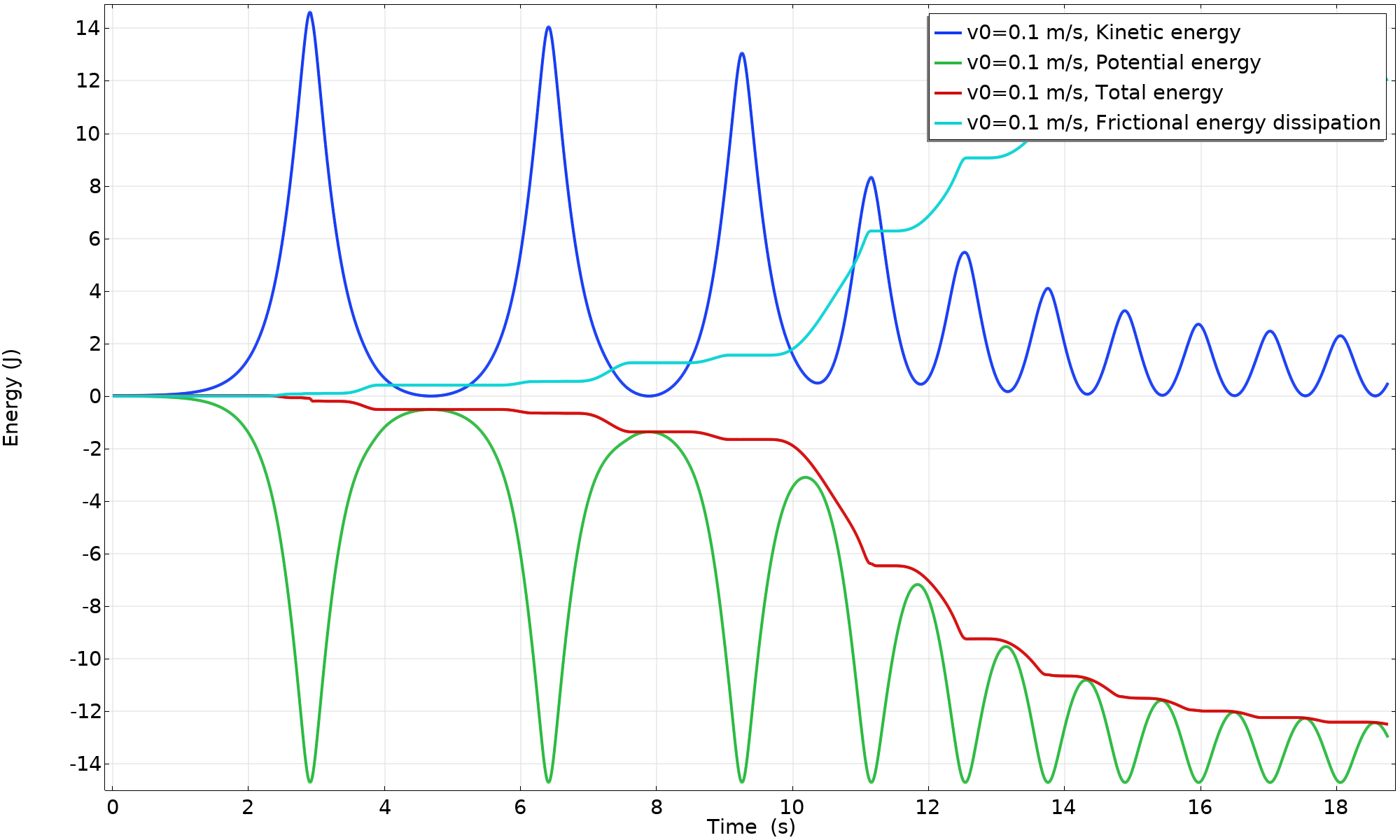
Energy balance (v_{0} = 0.1 \ m/s, \mu = 0.3).
Concluding Remarks
Note that the 2D animations shown above can be expanded into 3D. Below, you can view this done for the animation of the motion where v_ \textsl {0} = 3.1 \ \text {m/s}.
Throughout this blog post, we have shown that the behavior of a hopping hoop is much more intricate than you may think at first sight. Analyze the behavior yourself by downloading the tutorial model using the button below:
Further Resources
Want to learn more about this hopping hoop phenomenon? Check out these resources:





Comments (3)
Ivar KJELBERG
March 18, 2023Hello Henrik,
As usual nice model, and a good example.
One little comment: to allow your formulas to be fully parametrised, I suspect your “Definitions Variable” Wg should read rather like:
Wg = g_const*mtot*((aveop1(y)-root.Rc)*gamma+aveop2(y)*(1-gamma))
But so long the parameter Rc=1[m] I suspect this value for Wg is fully valid, as designed.
Another comment is that as you set the density rho to “0” and use an added mass, your internal variables for the inertia Iz are “0” or fail for the total mass (as there is a +eps trick missing in the calculation og mdb.rd1.m and mdb.rd2.m) and that your internal inertia Iz variable does not take into account the added masses (this I understand is by design in COMSOL).
Sincerely,
Ivar
Henrik Sönnerlind
March 20, 2023 COMSOL EmployeeHi Ivar,
Thanks for your comments. I have replaced the file in Application Gallery with one where the parametrization is fixed according to your suggestion.
The reason I did not assign a mass density to the ring, but rather used an Added Mass feature, is that I wanted the mass properties of an ideal ring with zero thickness. Anyway, we will look into those comments about mass evaluation.
Regards,
Henrik
Ivar KJELBERG
March 21, 2023Hi Henrik,
Thanks for that, I have noticed that many people miss the fact that added mass are not included (by default) in the inertia calculations, sometimes they even forget to add the forces introduced by these added masses features, which also have to be added manually, as you have done in your model. I do understand your way of NOT including them by default, sometimes the true desired of the user is not clear either. Perhaps it’s worth to highlight this even better in the documentation, still one needs to RTFM … 🙂
Sincerely ,
Ivar