
Each year, tennis players from around the world compete at the U.S. Open, one of the oldest and largest tennis tournaments. With the 2015 tournament approaching, I found myself reflecting on my own experiences playing tennis, particularly how the feeling you get after hitting the ball is never quite the same. Is this simply a figment of the imagination or is there a physical answer? As I will explain here, so-called “sweet spots” can account for this feeling.
The Vibration Node of a Tennis Racket
In mechanical vibration theory, the vibrations nodes are defined as the points that never move when a wave is passing through them. Because of a wave created by the impact of a ball hitting a racket, the racket will, in turn, begin to oscillate and vibrate. By looking at the mode shapes of the racket — held by a player at the end of the grip — we can identify points where the vibration motion is zero (i.e., where the magnitude is zero at any time during vibration). Here are the first three mode shapes of a tennis racket computed with COMSOL Multiphysics:
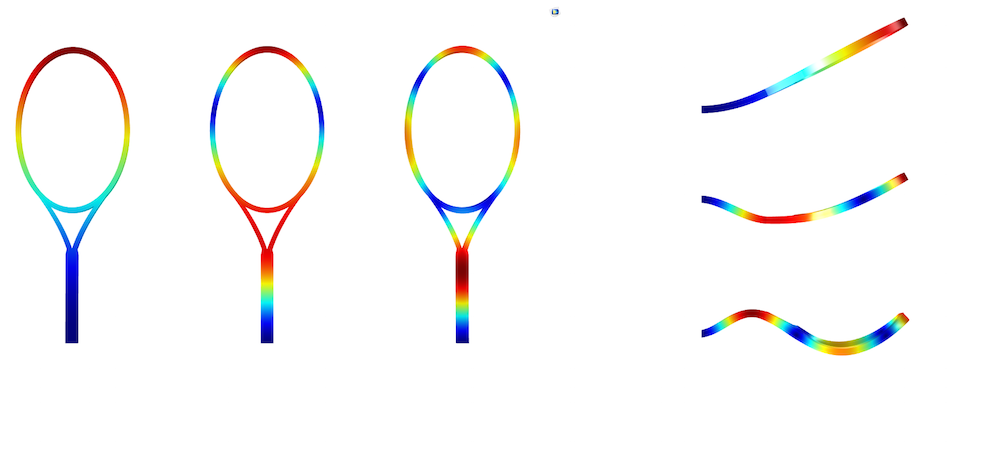
The first three mode shapes of a tennis racket, from left to right and top to bottom. The fundamental mode is at 15 Hz, the second mode is at 140 Hz, and the third mode is at 405 Hz.
As illustrated above, many different points feature this behavior. So why am I talking as if there is only one vibration node? In reality, there is actually an infinite number of vibration nodes. Upon impact, the ball generates an infinite number of harmonic series at different frequencies. An infinite number of frequencies are excited at one time, but which vibration node is the “sweet spot”? Is it the fundamental mode shape vibration node or is it a node that results from the crossing of different harmonics?
The fundamental mode vibration node cannot be the sweet spot for an obvious reason: It is located at the grip. Try hitting the ball with the grip to pass it over the net. If you are very lucky, you may succeed, but most likely, you won’t. The second vibration mode, meanwhile, has two nodes: one at the grip and one on the strings near the frame head. The latter is considered the sweet spot. Any player that hits the ball at this point will feel almost no vibration during impact.
There are, of course, vibration nodes on the strings for higher modes, as depicted in the third mode from the simulations above. However, as the natural frequency of the mode increases, the magnitude of the vibration drastically decreases. The graph below shows the frequency response of a sinusoidal load of 5 ms — approximately the duration of a ball’s impact upon hitting a racket — on a beam-like structure. For frequencies higher than 300 Hz, the magnitude is almost zero. That is, the influence of the third mode or higher is negligible. No matter where the ball strikes, even at points where the magnitude of the mode shape has reached its maximum, the higher modes will not have any influence at all because they are not excited.
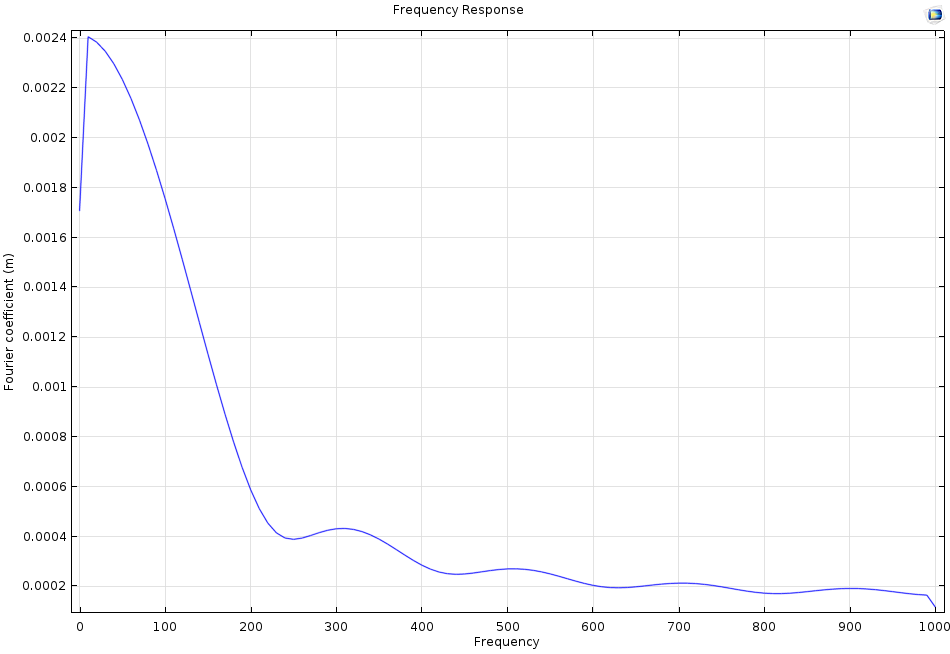
A plot showing the frequency response of a sinus load of 5 ms.
A Tennis Racket’s Center of Percussion
When the ball hits the tennis racket near one end, with no other force acting on it, the racket will rotate about an axis toward the other end. As the point where the ball strikes the racket becomes closer to the center of mass, the distance from the axis of rotation will decrease. In a case where the ball hits the center of mass, the racket will translate without any rotation. The center of rotation is, from a mathematical point of view, at an infinite distance from the racket.
That said, it is possible to find an impact location that produces a center of rotation near the end of the grip where the player holds the equipment. We can find a location at a certain distance from the center of mass where the ball hits the racket and results in a center of rotation near the end of the grip. Referred to as the center of percussion (COP), this location is sometimes considered a sweet spot as well. No force is applied to the hands, as the racket rotates about a center of rotation near the end of the grip, avoiding the player’s hands.

Compared to older wooden tennis rackets from the 1970s, modern forms of this equipment feature a much larger head. This new design element has been used to move the center of percussion near the middle of the strings rather than by the racket’s frame. Image by CORE-Materials, via Wikimedia Commons.
Let’s now take a quick look at what happens from a mechanical standpoint. For this purpose, we assume that the racket can be modeled as a rigid beam-like structure.
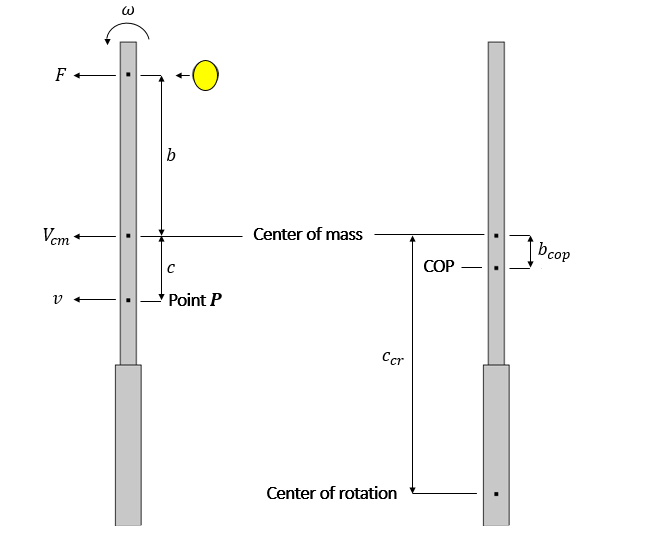
Sketch of the beam-like structure. The parameters used in the following equations are defined in this figure.
A force F applied to a free beam of mass M at a distance b from the center of mass implies that the center of mass translates at a speed V_{cm}. From Newton’s second law,
Moreover, a torque is generated by the force F about the center of mass:
where I is the beam moment of inertia along the rotation axis and \omega is the angular velocity. Consider P, a point at a distance c from the center of mass. The speed v of this point is v=V_{cm}-c\omega, leading to:
Since the center of rotation corresponds to the point where there is no translational acceleration, the COP is at a distance b_{cop} from the center of mass, which is given by
where c_{cr} is the distance between the center of rotation and the center of mass. Given that the distance between the center of mass and the ideal center of rotation (at the grip end) is known, it is rather straightforward to determine the position of the COP for a particular racket shape.
The Power Point
The power point, sometimes called the third sweet spot, is the best bouncing point. In other words, this is where the ball achieves the most bounce upon contact. From a mathematical standpoint, the power point is defined as the point with the highest coefficient of restitution (COR), the ratio of the rebound height to the incident height of the ball. The coefficient of restitution is quite useful in the sense that it is the result of all of the design elements that affect the speed of the ball. Design engineers do not need to know the influence of each parameter, as the COR provides a combined overview of all of these factors.
The power point is located at the throat of the racket, near the center of mass. The closer the point is to the throat, the greater the stiffness and the lower the energy loss during racket deformation. When a ball hits a racket, the impact energy is divided into kinetic energy and elastic energy (energy of deformation) throughout the ball, racket, and strings. At the power spot, deformation is very small, causing the racket to give almost all of the kinetic energy back to the ball.
The power spot is very useful when returning a fast serve. Indeed, if you must return a fast serve, you do not have much time to move your racket and prepare your stroke, so you will return the ball as it comes. However, it is important to note that the closer the ball comes to the power spot, the better your stroke will be.
The Dead Spot
One last interesting spot on the racket that I’d like to mention is the dead spot. When a ball strikes the dead spot, the ball will not bounce at all. All of the ball’s energy is given to the racket and no energy is given back to the ball. This is due to the fact that the effective mass of the racket at the dead spot — usually close to the tip — is equal to the mass of the ball. Mechanically speaking, the ratio between the resulting force and the acceleration at the dead spot is equal to the mass of the ball.
To better understand the physical phenomena at hand, let’s imagine the ideal collision between a rigid ball at an initial speed V_0 and another rigid ball, initially at rest, that features the same mass m. The conservation of energy and the conservation of momentum lead to:
Therefore, it turns out that:
If a ball collides with another ball that is of the same mass but at rest, the ball will stop dead and give all of its energy to the other ball. Thus, when a ball hits the dead spot of a racket at rest, the ball will not bounce at all. This would be a very bad spot to use when trying to return a serve. On the other hand, when you actively hit a stationary ball, as in your own serve, the dead spot will provide a high momentum transfer of energy from the racket to the ball.
Then, when it is your turn to serve, what is the optimal point? This is not only determined by the mathematics of sweet spots. In most cases, the answer would be rather close to the tip. Because of the way you move your arm, the racket will feature a significantly higher speed at the tip than at the throat. Thus, the optimal point is determined by a combination of high impact speed and good momentum transfer properties.
Game-Set-Match
We have now gained insight into the physical meaning behind the three well-known sweet spots of a tennis racket. At the vibration node, the uncomfortable vibration that tennis players feel over their hand and arm is minimal. At the center of percussion, the initial shock to the player’s hand is also minimal. Lastly, at the power point, the ball rebounds with the maximum level of speed.

The location of the sweet spots on a tennis racket.
Before You Hit the Court…
Perfect your game; check out these additional resources for improving your tennis skills:
- Tennis Science for Tennis Players, H. Brody.
- “Physics of the tennis racket“, H. Brody.
- “Physics of the tennis racket II: The “sweet spot“, H. Brody.
- “Physics of the tennis racket III: The ball-racket interaction“, H. Brody.
Read More About the Science of Sports
- Simulation provides a deeper understanding of the physics behind a number of other sports. Browse our Physics of Sports blog posts to learn more.





Comments (6)
Subhassh M
March 16, 2018Nice
Ruja ignotava
August 9, 2020Such a Great info regarding Racquet’s. i also purchase rackets before some days from Best Badmintion racquets after getting info. Thanks Alot.
John Luke
August 21, 2021I recently bought my favorite tennis rackets from a review website using the information you provided about tennis racquets and sweet spots. I appreciate the effort you put in.
Mohit Malhotra
August 27, 2021Great Article! I am also a blogger in badminton. Please check this blog also.
Rajni Bisht
November 30, 2021Enjoyed reading the article above, really explains everything in detail, the article is very interesting and effective. Thank you and good luck with the upcoming articles. And to know more about tennis rackets check out my site Sports Uncaged .
RacquetGuys RacquetGuys
March 24, 2023Thanks bro for quoting me.
I fully agree to your theory, it’s as simple as that. I picked up tennis last year and facing lots of issue, then one of my fiend’s dad told me about Racquetguys website. I am shocked that they sell all type of racquets which is latest in market. I purchase my Wilson clash 100 (295gm) and now I am at improver level. Thank you! That is helpful to know – much appreciated.