
Wenn Sie zum ersten Mal versuchen, eine Partikelverfolgungssimulation mit sehr kleinen Partikeln in einem Fluid durchzuführen – in der Regel mit einem Durchmesser von einigen zehn Mikrometern oder weniger – werden Sie vielleicht feststellen, dass der zeitabhängige Löser viel kürzere Zeitschritte als üblich verwendet. Dies ist häufig darauf zurückzuführen, dass die Bewegungsgleichungen der Partikel eine numerische Steifheit aufweisen. In diesem Blog-Beitrag stellen wir das Konzept der Steifheit in Bezug auf die Partikelsimulation vor und geben dann einige Richtlinien für die Auswahl der richtigen Gleichungsformulierung basierend auf der Partikelgröße.
Beispiel: Schwerkraftwirkung auf kleine Kugeln
Betrachten wir ein kleines kugelförmiges Teilchen, das mit einer gleichmäßigen Geschwindigkeit u (SI-Einheit: m/s) durch ein umgebendes Fluid fällt. Das Teilchen folgt dem zweiten Newtonschen Bewegungsgesetz,
(1)
wobei
- mp (SI-Einheit: kg) die Masse des Teilchens
- q (SI-Einheit: m) der Positionsvektor des Teilchens und
- Ft (SI-Einheit: N) die auf das Teilchen wirkende Gesamtkraft ist
Für ein Teilchen, das in einem Fluid absinkt, ist die Gesamtkraft die Summe der Schwerkraft Fg und des Strömungswiderstands FD,
(2)
\qquad
\mathbf{F}_\textrm{D} = 3\pi \mu d_\textrm{p}\left(\mathbf{u}-\mathbf{v}\right)
wobei
- ρp (SI-Einheit: kg/m3) die Dichte des Teilchens
- ρ (SI-Einheit: kg/m3) die Dichte des umgebenden Fluids
- g (SI-Einheit: m/s2) die Beschleunigung aufgrund der Schwerkraft (etwa 9.8 m/s2 vom Meeresspiegel abwärts)
- μ (SI-Einheit: Pa s) die dynamische Viskosität des umgebenden Fluids
- dp (SI-Einheit: m) der Durchmesser des Teilchens
- u (SI-Einheit: m/s) die Geschwindigkeit des umgebenden Fluids und
- v (SI-Einheit: m/s) die Geschwindigkeit des Teilchens ist (v ≡ dq/dt)
Der Term (ρp – ρ)/ρp im Ausdruck für die Schwerkraft steht für den Auftrieb. Er nähert sich 1 an, wenn die Teilchen viel schwerer sind als das Fluid, das sie verdrängen – wie zum Beispiel feste Partikel in Luft. Er nähert sich 0 an, wenn die Teilchen und das umgebende Fluid die gleiche Dichte haben. In diesem Fall werden die Teilchen als auftriebsneutral bezeichnet.
Der hier verwendete Ausdruck für den Strömungswiderstand stammt aus dem Gesetz von Stokes. Dieses Gesetz ist geeignet, wenn die relative Reynolds-Zahl des Teilchens sehr klein ist,
\textrm{Re}_\textrm{r} \equiv \frac{\rho d_\textrm{p}\left|\mathbf{u}-\mathbf{v}\right|}{\mu} \ll 1was für kleinere Teilchen wahrscheinlicher ist.
Nehmen wir an, dass die Teilchen ihre Größe nicht ändern (also sind dp und mp konstant). Die Masse einer Kugel ist
(3)
Durch die Kombination der Gleichungen 1–3 erhalten wir einen vereinfachten Ausdruck für die Bewegungsgleichung des Teilchens,
(4)
=
\frac{\rho_\textrm{p}-\rho}{\rho_\textrm{p}}\mathbf{g}
+
\frac{1}{\tau_\textrm{p}}\left(\mathbf{u}-\mathbf{v}\right)
wobei die Konstante τp eingeführt wurde,
τp besitzt Zeiteinheiten und wird die Lagrangesche Zeitskala oder die Reaktionszeit der Teilchengeschwindigkeit genannt, aus Gründen die bald deutlich werden.
Zur weiteren Vereinfachung nehmen wir an, dass das umgebende Fluid in Ruhe ist (u = 0) und das Teilchen anfangs ebenfalls (q = 0 und v = 0 zum Zeitpunkt t = 0). Nehmen wir außerdem an, wir richten unser Koordinatensystem so aus, dass der Gravitationsvektor in die –y-Richtung zeigt. Dann wird, ausgehend von Gleichung 4, die Gleichung für die y-Komponente der Teilchenposition zu
(5)
=
-\frac{\rho_\textrm{p}-\rho}{\rho_\textrm{p}}g-\frac{1}{\tau_\textrm{p}}v_y
Die exakte oderanalytische Lösung für Gleichung 5 mit den Anfangsbedingungen qy = 0 und vy = 0, ist
q_y &= -v_\textrm{t}\left\{t+\tau_\textrm{p}\left[\exp\left(-\frac{t}{\tau_\textrm{p}}\right)-1\right]\right\}\\
v_y &= -v_\textrm{t}\left[1-\exp\left(-\frac{t}{\tau_\textrm{p}}\right)\right]\\
\end{aligned}
wobei vt die Endgeschwindigkeit ist,
Umwandlung in dimensionslose Variablen
Um besser zu verstehen, wie das Teilchen während der ersten Vielfachen von τp beschleunigt, können wir die Zeit, Position und Geschwindigkeit (t, qy, vy) durch die entsprechenden dimensionslosen Größen (t‘, qy‘, vy‘) ersetzen, die wie folgt definiert sind:
q_y^{\prime} \equiv \frac{q_y}{v_\textrm{t}\tau_\textrm{p}} \quad\quad \\
v_y^{\prime} \equiv \frac{v_y}{v_\textrm{t}}
Das Einsetzen dieser dimensionslosen Variablen in die analytische Lösung ergibt
q_y^{\prime} &= -t^{\prime}-\exp\left(-t^{\prime}\right)+1\\
v_y^{\prime} &= -1+\exp\left(-t^{\prime}\right)\\
\end{aligned}
In der folgenden Abbildung werden die dimensionslose Position und Geschwindigkeit als Funktionen der dimensionslosen Zeit t‘ dargestellt. Dieser Plot veranschaulicht, dass sich die Teilchengeschwindigkeit asymptotisch der Endgeschwindigkeit nähert, wobei der Großteil der Beschleunigung während der ersten paar Vielfachen der Lagrangeschen Zeitskala τp stattfindet. Die Teilchenposition scheint sich nach dieser anfänglichen Beschleunigungsperiode linear zu ändern.
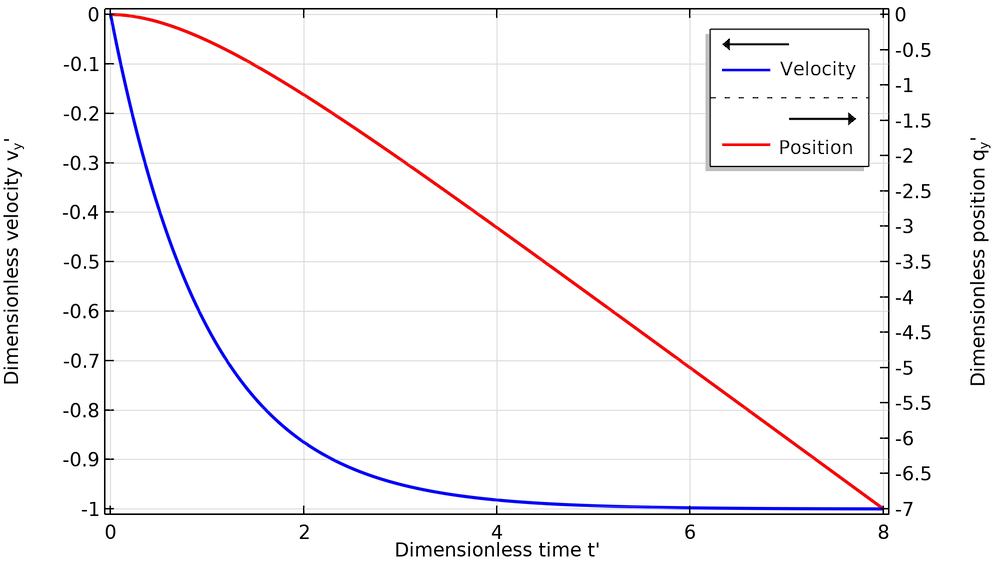
Plot der dimensionslosen Position und Geschwindigkeit eines Teilchens, das sich aus dem Ruhezustand heraus durch die Schwerkraft absetzt.
Zeitskalen für typische Teilchengrößen
Um eine bessere Vorstellung von den Zeitskalen zu bekommen, die bei der Teilchenbeschleunigung eine Rolle spielen, stellen Sie sich vor, die Teilchen seien Quarzglasperlen mit einer Dichte von etwa 2200 kg/m3. Die folgende Tabelle enthält einige Werte für die Lagrangesche Zeitskala in Luft und in Wasser für verschiedene Teilchengrößen.
| Fluid | Durchmesser des Teilchens (μm) | Dynamische Viskosität des Fluids (Pa s) | Dichte des Fluids (kg/m3) | Reaktionszeit (s) |
Endgeschwin digkeit (m/s) |
|---|---|---|---|---|---|
| Water | 1 | 1.009 × 10-3 | 998.2 | 1.2 × 10-7 | 6.5 × 10-7 |
| Water | 20 | 1.009 × 10-3 | 998.2 | 4.8 × 10-5 | 2.6 × 10-4 |
| Water | 50 | 1.009 × 10-3 | 998.2 | 3.0 × 10-4 | 1.6 × 10-3 |
| Air | 1 | 1.814 × 10-5 | 1.204 | 6.7 × 10-6 | 6.6 × 10-5 |
| Air | 20 | 1.814 × 10-5 | 1.204 | 2.7 × 10-3 | 2.6 × 10-2 |
| Air | 50 | 1.814 × 10-5 | 1.204 | 1.7 × 10-2 | 0.17 |
Die Abhängigkeit von τp vom Quadrat des Durchmessers bedeutet, dass große Teilchen eine viel längere Reaktionszeit und eine viel höhere Endgeschwindigkeit als kleine Teilchen haben. Dies hat zwei wesentliche Konsequenzen:
- Große Teilchen fallen viel schneller zu Boden als kleine Teilchen.
- Wenn große Teilchen mit einer gewissen Anfangsgeschwindigkeit in ein Fluid geschleudert werden, folgen sie ballistischen Bahnen, die eine beträchtliche Strecke zurücklegen können, bevor die Widerstandskraft sie abbremst. Im Gegensatz dazu erreichen kleinere Teilchen viel schneller die Geschwindigkeit des Fluids. Wenn sie sich ausbreiten, ist dies eher auf die turbulente Diffusion des umgebenden Fluids zurückzuführen.
Numerisches Particle Tracing
Im vorherigen Abschnitt hatten wir das Glück, dass Gleichung 4 eine exakte analytische Lösung hatte. Eine exakte Lösung war nur aufgrund aller vereinfachenden Annahmen möglich, insbesondere aufgrund der Tatsache, dass die Fluidgeschwindigkeit u überall Null war. In den meisten realen Systemen ist die Geschwindigkeit des umgebenden Fluids nicht nur nicht Null, sondern auch räumlich ungleichmäßig, was es sehr unwahrscheinlich macht, dass sich eine exakte Lösung mit Stift und Papier finden lässt.
Bei allgemeineren Problemen können wir auf numerische Simulationen zurückgreifen, um eine ungefähre Antwort zu erhalten. Die Grundidee besteht darin, dass wir bei gegebener Anfangsposition des Teilchens q0 und seiner Anfangsgeschwindigkeit v0 zum Anfangszeitpunkt t = 0 numerische Zeitschrittverfahren verwenden, um die Lösung in einer Reihe von diskreten Zeitschritten t1, t2, t3 usw. anzunähern. Zu diesem Zweck wurden zahlreiche verschiedene Time-Stepping-Algorithmen entwickelt, von denen viele in der COMSOL® Software verfügbar sind.
Die numerische Lösung einer Reihe von Differentialgleichungen führt zu einem gewissen Fehler – der Differenz zwischen der realen Teilchenbewegung und der berechneten numerischen Lösung. Während man normalerweise nicht darauf hoffen kann, eine perfekte Lösung aus einer numerischen Simulation zu erhalten, ist es ein realistischeres Ziel, dass die simulierte Teilchenbewegung genauer wird, wenn die Zeitintervalle (t1, t2 – t1, t3 – t2, etc.) kleiner werden.
Der Nachteil ist, dass Sie bei kleineren Zeitschritten mehr Zeitschritte benötigen, um dieselbe Ausgabezeit zu erreichen. Letztendlich kann dies zu einer spürbaren Erhöhung der Lösungszeit führen, d. h. der Zeit, die der Benutzer auf den Abschluss der Simulation warten muss. Ingenieure, die mit numerischer Simulation arbeiten, müssen immer ein angemessenes Gleichgewicht zwischen Lösungsgenauigkeit und Lösungszeit anstreben.
Das Interface Particle Tracing for Fluid Flow, das mit dem Particle Tracing Module, einem Add-On zu COMSOL Multiphysics®, erhältlich ist, simuliert die Bewegung einzelner Partikel in einem umgebenden Fluid, indem es das zweite Newtonsche Gesetz numerisch löst. Auf einer grundlegenden Ebene löst dieses Interface Gleichung 1, während Sie auf der rechten Seite eine Vielzahl unterschiedlicher Kräfte hinzufügen können. Es enthält auch viele Optionen zum Festlegen der anfänglichen Teilchenposition und -geschwindigkeit sowie zur Erkennung und Behandlung von Teilchenkollisionen mit Oberflächen in der umgebenden Geometrie.
Umgang mit kleinen Teilchen und langen Zeitskalen
In vielen praktischen Anwendungen ist die Bandbreite der gewünschten Lösungszeiten für ein Partikelverfolgungsmodell viel größer als die Lagrangesche Zeitskala τp. Nehmen wir zum Beispiel an, dass wir die Bewegung einiger Quarzglaspartikel mit einer Größe von 20 µm in Wasser über eine Gesamtsimulationszeit von 1 Sekunde verfolgen wollen. Wie wir in der vorherigen Tabelle gesehen haben, beträgt die Lagrangesche Reaktionszeit für solche kleinen Partikel in Wasser etwa 5 × 10-5 Sekunden, sodass die Gesamtsimulationszeit etwa 2000 τp beträgt. Wenn wir noch kleinere Partikel über einen Zeitraum von Minuten oder Stunden verfolgen wollten, können wir uns leicht Szenarien vorstellen, in denen unsere Gesamtsimulationszeit millionenfach größer als τp wäre.
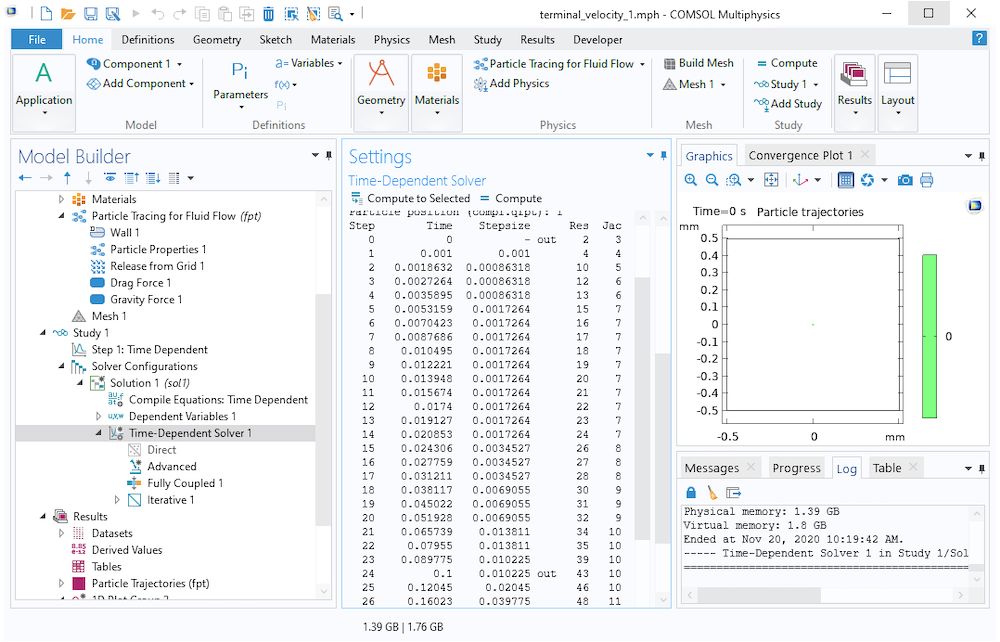
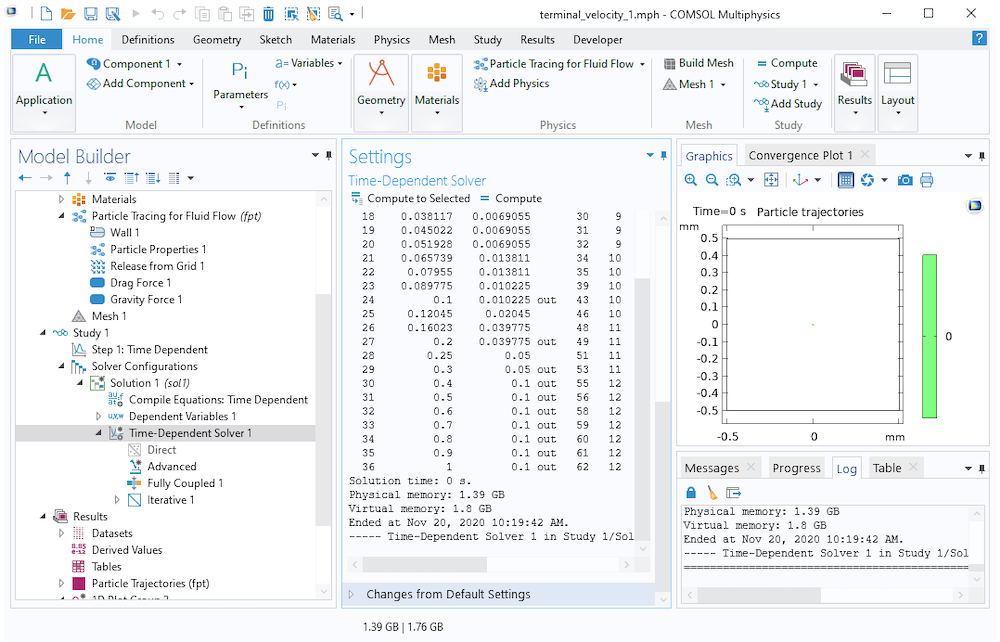
Der folgende Screenshot zeigt ein Protokoll der Zeitschritte, die der zeitabhängige Löser bei der Verfolgung dieser 20-µm-Partikel durchläuft. Der Bereich der Ausgabezeiten im Knoten Step 1: Time Dependent wurde auf range(0,0.1,1) festgelegt, was bedeutet, dass nur Ausgaben in Vielfachen von 0,1 s gespeichert werden. Dies hindert den Löser jedoch nicht daran, bei Bedarf kleinere Zeitschritte zu verwenden, um eine genaue Lösung zu erhalten. Wie hier gezeigt, beginnt der Löser mit Zeitschritten in der Größenordnung von 1 ms oder kleiner und nimmt dann allmählich größere Schritte vor, wenn sich das Teilchen seiner Endgeschwindigkeit nähert.
In COMSOL Multiphysics® verwenden die Particle-Tracing-Physik-Interfaces im Allgemeinen den Time-Stepping-Algorithmus Strict, der erfordert, dass zumindest einige der vom Löser ausgeführten Schritte mit den Ausgabezeiten übereinstimmen, wie z. B. Schritt 24 unten. Dies ist keine allgemeine Anforderung; bei einigen Physik-Interfaces können die Ausgabezeiten durch Interpolation zwischen den nächsten Schritten des Lösers ermittelt werden.
Gegen Ende der Studie können die Zeitschritte recht groß sein, da das Teilchen kaum noch beschleunigt wird. Letztendlich benötigt der Löser 24 Zeitschritte, um die erste Ausgabezeit bei 0,1 s zu erreichen, aber nur 12 weitere Zeitschritte, um die Endzeit bei 1 s zu erreichen.
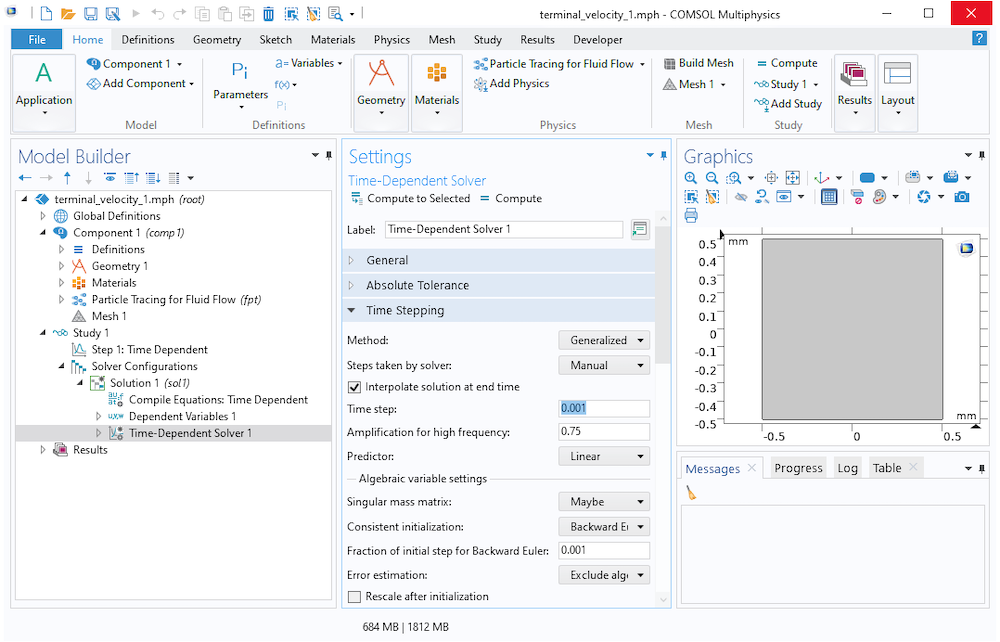
Die Bewegungsgleichung eines Teilchens, das sich unter dem Einfluss der Schwerkraft absetzt, ist ein Beispiel für eine steife gewöhnliche Differentialgleichung. Die Standard-Zeitschrittmethode, die in den meisten Partikelverfolgungsmodellen verwendet wird, heißt Generalized alpha und ist ein implizites Zeitschrittverfahren zweiter Ordnung, das sich gut für die Behandlung steifer Probleme eignet. Wenn zusätzliche Stabilität erforderlich ist, gibt es einen numerischen Dämpfungsterm, der in den Einstellungen des Lösers Time-Dependent angepasst werden kann und als Amplification for high frequency bezeichnet wird. Aus diesem Grund können die Zeitschritte größer werden, wenn sich die Partikelgeschwindigkeit der Endgeschwindigkeit nähert. (Im Gegensatz dazu benötigt die explizite Runge-Kutta-Methode RK34 7425 Schritte, um dasselbe Problem zu lösen!)
Wenn jedoch Teilchen zu verschiedenen Zeiten in das Simulationsgebiet eintreten würden oder wenn die Geschwindigkeit des Fluids im Hintergrund räumlich ungleichmäßig wäre (sodass die Teilchen später in der Studie noch beschleunigen könnten), müsste der Löser möglicherweise bis zum Endzeitpunkt weiterhin so kleine Zeitschritte ausführen. Wenn wir versuchen, sehr kleine Partikel über einen langen Simulationszeitraum zu verfolgen, werden diese Studien letztendlich eine beträchtliche Menge an Rechenzeit in Anspruch nehmen, da der Löser Hunderttausende oder sogar Millionen von Schritten ausführt.
Ein eng verwandtes Phänomen, das für neue Nutzer der COMSOL® Software verwirrend sein kann, ist die Freisetzung von Teilchen in das Simulationsgebiet mithilfe der Randbedingung Inlet. Angenommen, diesen Teilchen wird eine Anfangsgeschwindigkeit zugewiesen, die in das Simulationsgebiet zeigt. Beachten Sie in den vorherigen Screenshots, dass die anfängliche Zeitschrittgröße (bei einer Gesamtsimulationszeit von 1 Sekunde) 1 Millisekunde betrug. Wenn die anfängliche Zeitschrittgröße immer noch viel größer als τp ist, könnte der Strömungswiderstand überkompensieren, was dazu führt, dass die Teilchengeschwindigkeit kurzzeitig die Richtung ändert und wieder auf den Rand am Einlass zeigt. In diesem Fall könnten die Teilchen fälschlicherweise eine Kollision mit dem Rand erkennen, wodurch sie dort stecken bleiben.
Umgang mit numerischer Steifheit in Particle-Tracing-Modellen
Es gibt zwei Hauptmethoden, um mit numerisch steifen Modellen der Teilchenbewegung in einem Fluid umzugehen – Modelle, bei denen der Abstand zwischen den Ausgabezeiten mehrere Größenordnungen größer ist als τp.
Die erste ist die „gewaltsame“ Methode: Weisen Sie den Löser einfach an, kleinere Zeitschritte zu verwenden. Wenn Sie keine überwältigende Menge an Ergebnissen mit potenziell riesigen Dateigrößen erzeugen möchten, können Sie die Ausgabezeiten unverändert lassen, aber in den Einstellungen für den zeitabhängigen Löser weiter unten in der Löser-Sequenz eine kleinere Schrittgröße oder maximale Schrittgröße angeben.
Der andere Ansatz, der seit COMSOL Multiphysics® Version 5.6 möglich ist, besteht darin, den Trägheitsausdruck aus Gleichung 4 zu streichen. Zunächst formulieren wir Gleichung 4 als ein Paar gekoppelter Gleichungen erster Ordnung,
\frac{\textrm{d} \mathbf{q}}{\textrm{d}t} &= \mathbf{v}\\
\frac{\textrm{d} \mathbf{v}}{\textrm{d}t} &= \frac{\rho_\textrm{p}-\rho}{\rho_\textrm{p}}\mathbf{g} + \frac{1}{\tau_\textrm{p}}\left(\mathbf{u}-\mathbf{v}\right)\\
\end{aligned}
Anstatt die Teilchenbewegung während der ersten paar Vielfachen von τp vollständig aufzulösen, nehmen wir nun einfach an, dass der Strömungswiderstand immer im dynamischen Gleichgewicht mit allen anderen Kräften steht.
(6)
+
\frac{1}{\tau_\textrm{p}}\left(\mathbf{u}-\mathbf{v}\right)
=
\mathbf{0}
Mit anderen Worten: Wir nehmen einfach an, dass das Teilchen sofort seine Endgeschwindigkeit erreicht. Dies ist eine angemessene Annäherung, wenn die Zeit, die benötigt wird, um sich der Endgeschwindigkeit zu nähern, um viele Größenordnungen kleiner ist als die gesamte Simulationszeit. Gleichung 6 kann nach v aufgelöst werden,
oder, allgemeiner gefasst,
(7)
wobei Fother die Summe aller Kräfte mit Ausnahme des Strömungswiderstands ist.
Dann müssen wir nur noch diesen Ausdruck für v über die Zeit integrieren, um die Teilchenposition q zu erhalten.
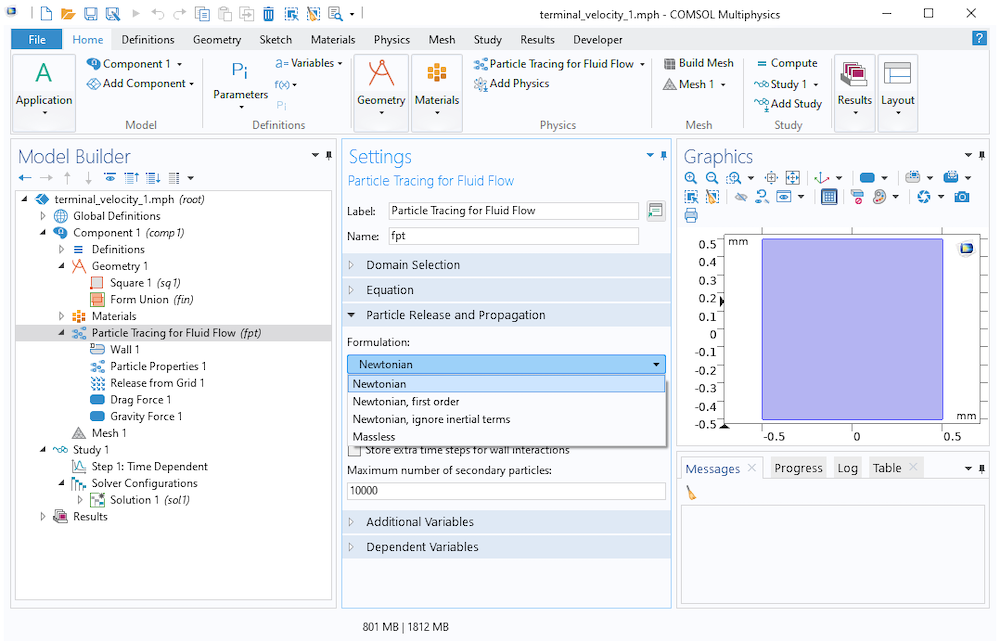
Um auszuwählen welches Gleichungssystem das Interface Particle Tracing for Fluid Flow lösen wird, navigieren Sie zum Abschnitt Particle Release and Propagation. Aus der Liste Formulation können Sie eine der folgenden Optionen wählen:
- Newtonian: Löst Gleichung 1
- Newtonian, first order: Teilt Gleichung 1 in ein Paar gekoppelter Gleichungen erster Ordnung für q und v und löst diese
- Newtonian, ignore inertial terms (verfügbar ab Version 5.6): Eine vereinfachte Formulierung, die die Geschwindigkeit mithilfe von Gleichung 7 definiert und dann nach q löst
- Massless: Eine noch weiter vereinfachte Formulierung, für die Sie v direkt angeben um nach q zu lösen
Beachten Sie, dass die Anzahl der verfügbaren integrierten Kräfte für die Formulierungen „Newtonian und Newtonian, first order etwas größer ist als für die Formulierung Newtonian, ignore inertial terms. Kräfte, die explizit von der Teilchengeschwindigkeit oder den relativen Positionen anderer Teilchen abhängen, wurden ausgeschlossen.
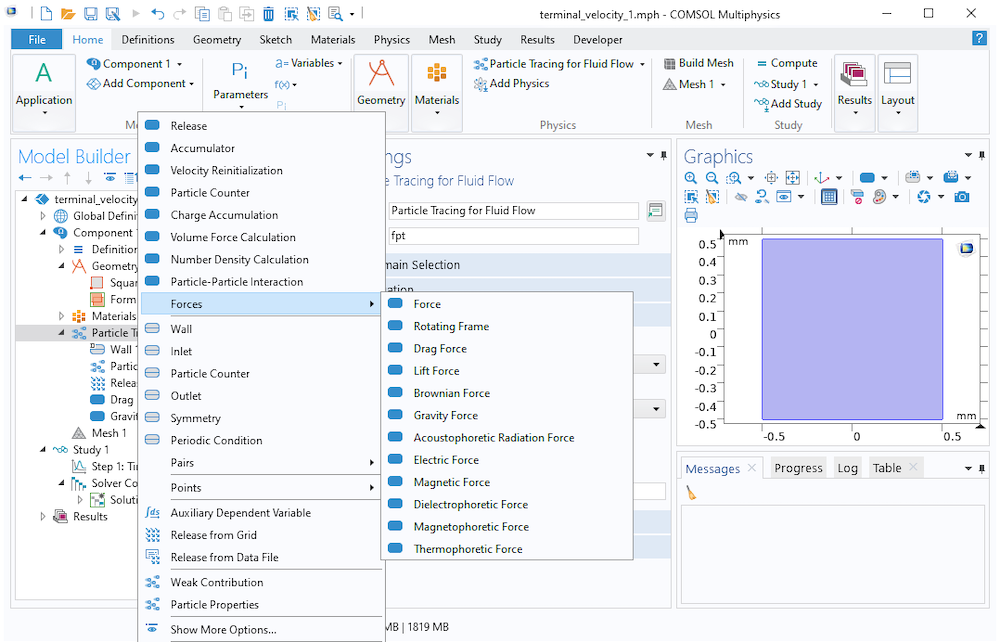
Verfügbare Kräfte für die Formulierung Newtonian .
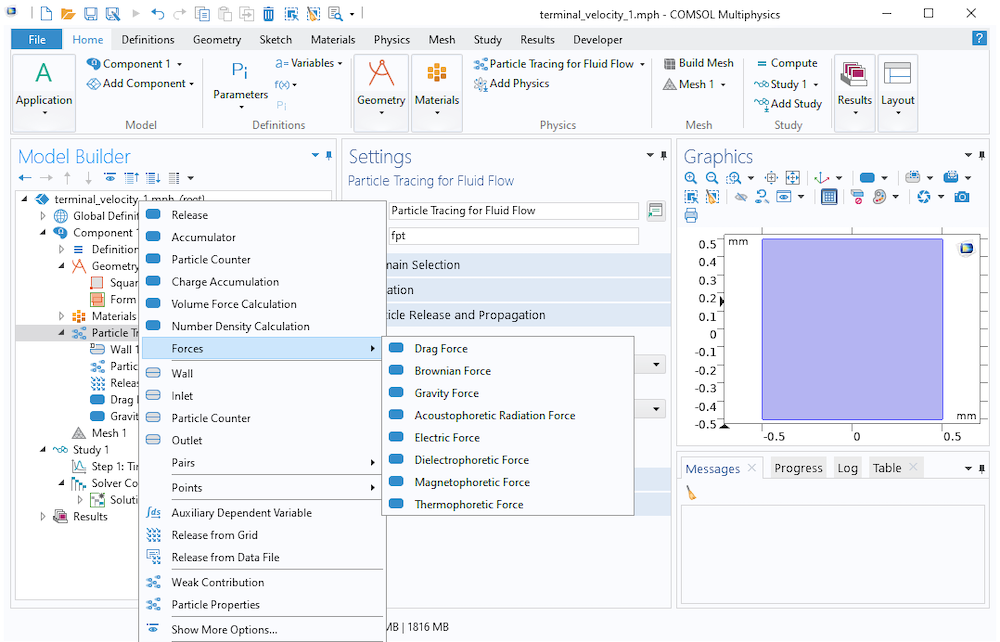
Verfügbare Kräfte für die Formulierung Newtonian, ignore inertial terms .
Die folgenden Beispiele aus der Application Library verwenden die Formulierung Newtonian, ignore inertial terms, um sehr kleine Partikel über einen langen Lösungszeitraum zu verfolgen:
- Teilchenbahnen in einem laminaren statischen Mischer
- Dielektrophoretische Trennung von Blutplättchen und roten Blutkörperchen
In diesen Beispielen wird die Formulierung Newtonian verwendet, da die Teilchen groß genug sind, damit die Trägheit einen signifikanten Einfluss auf die Teilchenbewegung hat:
Abschließende Gedanken zu Particle Tracing in Fluiden
Wenn Sie die Bewegung kleiner Partikel in einem Fluid mithilfe des Interfaces Particle Tracing for Fluid Flow simulieren, sollten Sie in der Regel zunächst die Lagrangesche Zeitskala τp schätzen, die mit den Partikeln verbunden ist,
und diese Zeitskala mit der Bandbreite der Lösungszeiten vergleichen, die Sie modellieren möchten.
Wenn Sie eine Verteilung verschiedener Teilchengrößen haben, nehmen Sie diese Schätzung auf der Grundlage der kleinsten Teilchengröße vor, da die kleinsten trägen Teilchen im Modell diejenigen sind, die bestimmen, wie numerisch steif die Bewegungsgleichungen sind.
Wenn Sie die Teilchenbewegung über einen Zeitraum vorhersagen möchten, der viel größer ist als die Reaktionszeit der Geschwindigkeit (sagen wir einfach um einen Faktor von mehreren Tausend oder mehr), dann sollten Sie überlegen, ob die Trägheit tatsächlich eine bedeutende Rolle bei der Teilchenbewegung spielt. Wenn nicht, können Sie die Option Newtonian, ignore inertial terms (verfügbar ab Version 5.6) wählen.
Wenn Sie dennoch die Trägheit berücksichtigen möchten, können Sie die Formulierung Newtonian oder Newtonian, first order verwenden. Beachten Sie jedoch, dass das zu lösende Gleichungssystem numerisch steif ist und Sie möglicherweise die Größe der Zeitschritte, die der Löser ausführt, manuell reduzieren müssen, um nichtphysikalische Schwingungen in der Teilchenposition und -geschwindigkeit zu verhindern.




Kommentare (0)