
Wenn Sie auf eine Schale aus Glas oder Metall schlagen, hören Sie einen Ton, dessen Intensität mit der Zeit abklingt. In einer Welt ohne Dämpfung würde der Ton ewig verweilen. In Wirklichkeit gibt es mehrere physikalische Prozesse, durch die sich die kinetische und elastische Energie in der Schale in andere Energieformen auflöst. In diesem Blogbeitrag gehen wir darauf ein, wie Dämpfung dargestellt werden kann und welche physikalischen Phänomene in schwingenden Strukturen zu Dämpfung führen.
Wie wird die Dämpfung quantifiziert?
Es gibt mehrere Möglichkeiten, wie die Dämpfung aus mathematischer Sicht beschrieben werden kann. Einige der bekanntesten Beschreibungen sind unten zusammengefasst.
Eine der offensichtlichsten Erscheinungsform der Dämpfung ist der Amplitudenabfall während freier Schwingungen, wie im Fall einer Klangschale. Die Abklinggeschwindigkeit hängt davon ab, wie groß die Dämpfung ist. Meist nimmt die Schwingungsamplitude exponentiell mit der Zeit ab. Dies ist der Fall, wenn der Energieverlust während eines Zyklus proportional zur Amplitude des Zyklus selbst ist.

Eine typische Klangschale. Bild von Sneharamm0han — Eigenes Werk. Lizensiert unter CC BY-SA 4.0, via Wikimedia Commons.
Beginnen wir mit der Bewegungsgleichung für ein System mit einem einzigen Freiheitsgrad (DOF) mit viskoser Dämpfung und ohne externe Lasten,
Nach Division mit der Masse m erhalten wir eine normierte Form, üblicherweise geschrieben als
Hier ist \omega_0 die ungedämpfte Eigenfrequenz und \zeta wird als Dämpfungsverhältnis bezeichnet.
Damit die Bewegung periodisch ist, muss das Dämpfungsverhältnis auf den Bereich 0 \le \zeta < 1. begrenzt werden. Die Amplitude der freien Schwingung in diesem System wird mit dem Faktor
abklingen, wobei T0 die Periode der ungedämpften Schwingung ist.
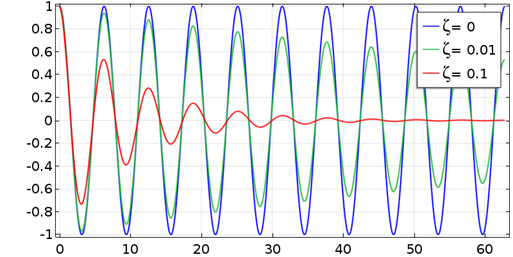
Abklingen einer freien Schwingung für drei verschiedene Werte des Dämpfungsverhältnisses.
Ein weiteres verwendetes Maß ist das logarithmische Dekrement δ. Dies ist der Logarithmus des Verhältnisses zwischen den Amplituden zweier aufeinanderfolgender Spitzen,
wobei T die Periode ist.
Die Beziehung zwischen dem logarithmischen Dekrement und dem Dämpfungsverhältnis ist
Ein weiterer Fall, in dem der Dämpfungseffekt eine wichtige Rolle spielt, ist, wenn eine Struktur einer harmonischen Anregung mit einer Frequenz nahe der Eigenfrequenz ausgesetzt ist. Genau bei Resonanz tendiert die Schwingungsamplitude gegen unendlich, es sei denn, das System ist gedämpft. Die tatsächliche Amplitude bei Resonanz wird ausschließlich durch die Dämpfung bestimmt.
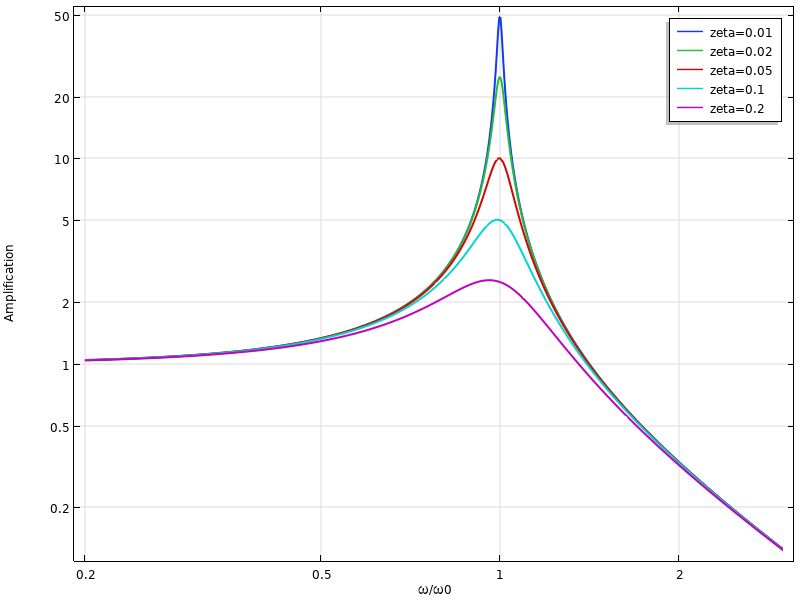
Verstärkung für ein Single-DOF-System bei verschiedenen Frequenzen und Dämpfungsverhältnissen.
Bei einigen Systemen, wie z. B. Resonatoren, ist es das Ziel, so viel Verstärkung wie möglich zu erreichen. Daraus ergibt sich ein weiteres beliebtes Dämpfungsmaß: der Qualitätsfaktor oder Q-Faktor. Er ist definiert als die Resonanzverstärkung. Der Q-Faktor ist mit dem Dämpfungsverhältnis wie folgt verknüpft
Ein weiterer Ausgangspunkt für die Beschreibung der Dämpfung ist die Annahme, dass eine gewisse Phasenverschiebung zwischen der aufgebrachten Kraft und der resultierenden Verschiebung oder zwischen Spannung und Dehnung besteht. Von Phasenverschiebungen zu sprechen, ist nur für eine stationäre harmonische Schwingung sinnvoll. Wenn man die Spannung gegenüber der Dehnung für eine ganze Periode aufzeichnet, erhält man eine Ellipse, die eine Hystereseschleife beschreibt.
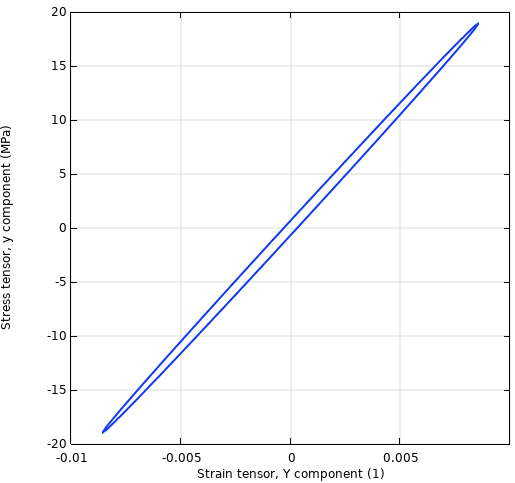
Spannungs-Dehnungs-Historie.
Man kann sich die Materialeigenschaften als komplexwertig vorstellen. Für einachsige lineare Elastizität kann die komplexwertige Spannungs-Dehnungs-Beziehung wie folgt geschrieben werden
Dabei wird der Realteil des Elastizitätsmoduls als Speichermodul und der Imaginärteil als Verlustmodul bezeichnet. Häufig wird der Verlustmodul durch einen Verlustfaktor, η, beschrieben, so dass
Hier kann E als Speichermodul E’ bezeichnet werden. Man kann auch eine andere Definition finden, in der E das Verhältnis zwischen der Spannungsamplitude und der Dehnungsamplitude ist, also
In diesem Fall
Diese Unterscheidung ist nur bei hohen Werten des Verlustfaktors wichtig.
Ein gleichwertiges Maß für die Verlustfaktordämpfung ist der Verlusttangens, definiert als
Der Verlustwinkel δ ist die Phasenverschiebung zwischen Spannung und Dehnung.
Die durch einen Verlustfaktor definierte Dämpfung verhält sich etwas anders als die viskose Dämpfung. Die Verlustfaktordämpfung ist proportional zur Verschiebungsamplitude, während die viskose Dämpfung proportional zur Geschwindigkeit ist. Daher ist es nicht möglich, die eine Zahl direkt in die andere umzurechnen.
In der folgenden Abbildung wird die Reaktion eines Single-DOF-Systems für die beiden Dämpfungsmodelle verglichen. Es ist zu erkennen, dass die viskose Dämpfung oberhalb der Resonanz eine höhere Dämpfung als die Verlustfaktordämpfung und unterhalb der Resonanz eine geringere Dämpfung voraussagt.
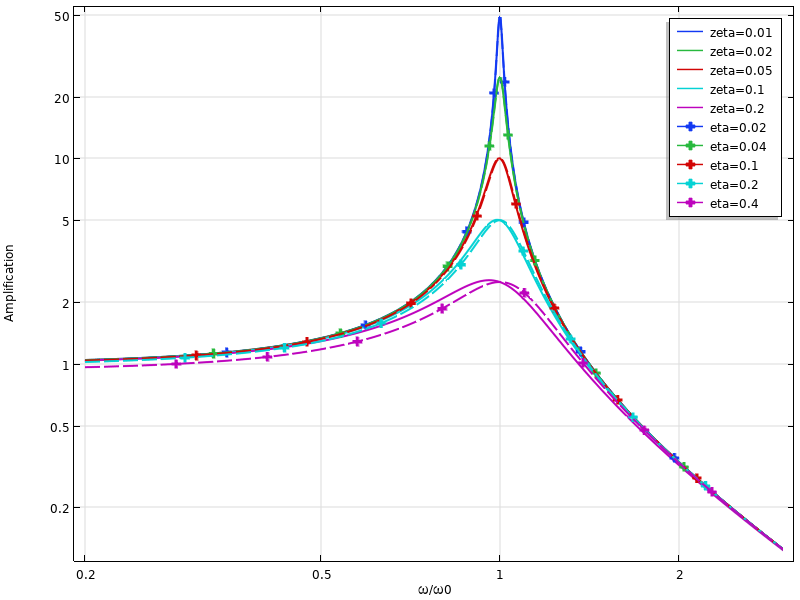
Vergleich des dynamischen Verhaltens bei viskoser Dämpfung (durchgezogene Linien) und Verlustfaktordämpfung (gestrichelte Linien).
Normalerweise wird die Umrechnung zwischen dem Dämpfungsverhältnis und der Verlustfaktordämpfung bei einer Resonanzfrequenz betrachtet, und dann ist \eta \approx 2 \zeta. Dies gilt jedoch nur für eine einzige Frequenz. In der folgenden Abbildung wird ein Zwei-DOF-System betrachtet. Die Dämpfungswerte wurden bei der ersten Resonanz angepasst, und es ist klar, dass die Vorhersagen bei der zweiten Resonanz erheblich abweichen.
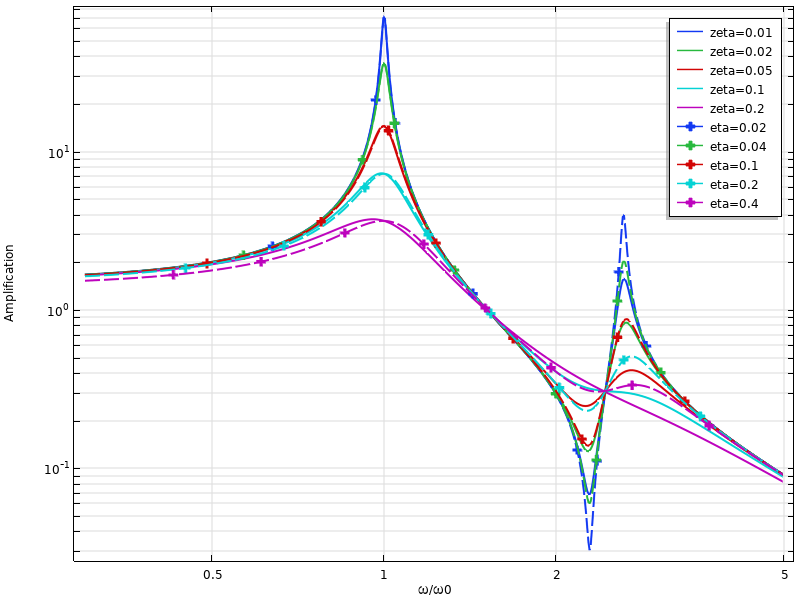
Vergleich des dynamischen Verhaltens bei viskoser Dämpfung und Verlustfaktordämpfung für ein Zwei-DOF-System.
Das Konzept des Verlustfaktors kann verallgemeinert werden, indem der Verlustfaktor in Form von Energie definiert wird. Es kann gezeigt werden, dass für das oben beschriebene Materialmodell die während eines Belastungszyklus dissipierte Energie
ist, wobei\varepsilon_a die Dehnungsamplitude ist.
Entsprechend beträgt die maximale elastische Energie während des Zyklus
Der Verlustfaktor lässt sich also in Form von Energie wie folgt ausdrücken:
Diese Definition der dissipierten Energie kann unabhängig davon verwendet werden, ob die Hystereseschleife tatsächlich eine perfekte Ellipse ist oder nicht — solange die beiden Energiegrößen bestimmt werden können.
Dämpfungsquellen
Aus physikalischer Sicht gibt es viele mögliche Quellen für Dämpfung. Die Natur neigt dazu, immer einen Weg zu finden, Energie zu dissipieren.
Interne Materialverluste
Alle realen Materialien geben unter Last eine gewisse Energie ab. Man kann sich das als eine Art innere Reibung vorstellen. Wenn man sich eine Spannungs-Dehnungs-Kurve für einen kompletten Belastungszyklus anschaut, wird sie keine perfekte gerade Linie zeichnen. Vielmehr sieht man etwas, das eher einer dünnen Ellipse ähnelt.
Häufig wird der Verlustfaktordämpfung eine geeignete Darstellung für die Materialdämpfung zugeschrieben, da die Erfahrung zeigt, dass der Energieverlust pro Zyklus eher schwach von der Frequenz und der Amplitude abhängt. Da die mathematische Grundlage für die Verlustfaktordämpfung jedoch auf komplexwertigen Größen beruht, liegt die Annahme einer harmonischen Schwingung zugrunde. Daher kann dieses Dämpfungsmodell nur für Analysen im Frequenzbereich verwendet werden.
Der Verlustfaktor für ein Material kann recht stark variieren, je nachdem, wie es im Einzelnen zusammengesetzt ist und welche Quellen Sie zu Rate ziehen. In der nachstehenden Tabelle sind einige grobe Schätzungen aufgeführt.
| Werkstoff | Verlustfaktor, η |
|---|---|
| Aluminium | 0.0001–0.02 |
| Beton | 0.02–0.05 |
| Kupfer | 0.001–0.05 |
| Glas | 0.0001–0.005 |
| Gummi | 0.05–2 |
| Stahl | 0.0001–0.01 |
Verlustfaktoren und ähnliche Dämpfungsbeschreibungen werden hauptsächlich dann verwendet, wenn die genaue Physik der Dämpfung im Material nicht bekannt oder nicht wichtig ist. Bei mehreren Materialmodellen, wie der Viskoelastizität, ist die Dissipation eine inhärente Eigenschaft des Modells.
Reibung in Gelenken
Es ist üblich, dass Strukturen z. B. durch Schrauben oder Nieten verbunden sind. Wenn die verbundenen Oberflächen während der Schwingung relativ zueinander gleiten, wird die Energie durch Reibung abgeführt. Solange sich der Wert der Reibungskraft selbst während des Zyklus nicht ändert, ist der Energieverlust pro Zyklus mehr oder weniger frequenzunabhängig. In diesem Sinne ist die Reibung vergleichbar mit internen Verlusten im Material.
Verschraubungen sind im Maschinenbau weit verbreitet. Das Ausmaß der Dämpfung, das bei Schraubverbindungen auftritt, kann je nach Konstruktion sehr unterschiedlich sein. Wenn eine geringe Dämpfung wichtig ist, sollten die Schrauben eng beieinander liegen und gut angezogen sein, damit ein makroskopischer Gleitvorgang zwischen den Verbindungsflächen vermieden wird.
Geräuschemissionen
Eine vibrierende Oberfläche verdrängt die umgebende Luft (oder ein anderes umgebendes Medium), so dass Schallwellen ausgesandt werden. Diese Schallwellen tragen einen Teil der Energie ab, was aus der Sicht der Struktur zu einem Energieverlust führt.

Ein Diagramm der Schallemission in einem Tonpilz-Schallwandler.
Ankerverluste
Oft ist ein kleines Bauteil an einer größeren Struktur befestigt, die nicht Teil der Simulation ist. Wenn das Bauteil vibriert, werden einige Wellen in der tragenden Struktur induziert und fortgetragen. Dieses Phänomen wird oft als Ankerverluste bezeichnet, insbesondere im Zusammenhang mit MEMS.
Thermoelastische Dämpfung
Selbst bei einer rein elastischen Verformung ohne Verlustleistung führt die Dehnung eines Materials zu einer geringfügigen Änderung seiner Temperatur. Eine lokale Dehnung führt zu einer Temperatursenkung, während eine Kompression eine lokale Erwärmung zur Folge hat.
Grundsätzlich handelt es sich dabei um einen reversiblen Prozess, d. h. die Temperatur kehrt auf den ursprünglichen Wert zurück, wenn die Spannung aufgehoben wird. In der Regel gibt es jedoch Gradienten im Spannungsfeld mit entsprechenden Gradienten in der Temperaturverteilung. Dies führt zu einem Wärmestrom von wärmeren zu kühleren Regionen. Wird die Spannung in einem späteren Teil des Belastungszyklus abgebaut, ist die Temperaturverteilung nicht mehr dieselbe wie bei der Aufladung. Daher ist es nicht möglich, lokal in den ursprünglichen Zustand zurückzukehren. Dies wird zu einer Quelle der Dissipation.
Der thermoelastische Dämpfungseffekt ist vor allem dann wichtig, wenn mit kleinen Längenskalen und hochfrequenten Schwingungen gearbeitet wird. Bei MEMS-Resonatoren kann die thermoelastische Dämpfung zu einer erheblichen Verringerung des Q-Faktors führen.
Dämpfungskomponenten
Manchmal enthält eine Struktur absichtlich diskrete Dämpfer, wie die Stoßdämpfer in einer Radaufhängung.

Stoßdämpfer. Bild von Avsar Aras — Eigenes Werk. Lizenziert unter CC BY-SA 3.0, durch Wikimedia Commons.
Diese Komponenten haben offensichtlich einen großen Einfluss auf die Gesamtdämpfung in einer Struktur, zumindest in Bezug auf einige Schwingungsformen.
Seismische Dämpfungselemente
Ein besonderer Fall, in dem viel Aufwand für die Dämpfung betrieben wird, sind Bauwerke in seismisch aktiven Gebieten. Es ist von größter Bedeutung, die Erschütterungen in Gebäuden zu reduzieren, wenn diese von einem Erdbeben getroffen werden. Der Zweck solcher Dämpfer kann sowohl darin bestehen, ein Bauwerk von seinem Fundament zu isolieren, als auch darin, die Schwingungen zu dämpfen.

Ein seismischer Dämpfer für ein städtisches Gebäude. Bild von Shustov — Eigenes Werk. Lizensiert unter CC BY-SA 3.0, durch Wikimedia Commons.
Weitere Informationen
Lesen Sie die Folgebeiträge zu diesem Blogbeitrag hier:






Kommentare (0)