
Das Katana ist ein legendäres Schwert, das erstmals vor mehreren Jahrhunderten von den Samurai benutzt wurde. Es ist vielleicht am besten für seine geschwungene Form und seine bemerkenswert scharfe Einzelschneide bekannt. In diesem Blog-Beitrag werden wir untersuchen, wie man mit der Software COMSOL Multiphysics® ein einfaches Modell eines Katanas erstellt und einen differentiellen Härtungsprozess simuliert, um einige seiner Eigenschaften zu erforschen.
Inhaltsverzeichnis
- Das berühmte Katana
- Das Metal Processing Module
- Differentialhärtung
- Die Multiphysik der Wärmebehandlung
- Das Material des Katanas
- Geometrie des Katanas
- Modellierung der Phasenumwandlung:
- Mechanische und thermische Materialeigenschaften
- Modellierung des Wärmetransports:
- Modellierung von Spannungen und Dehnungen
- Ergebnisse
- Anwendung
Das berühmte Katana
Nur wenige Waffen sind so berühmt wie das Katana, die Waffe der japanischen Samurai. Das Schwert, das für seine Schärfe berüchtigt ist und nur als letztes Mittel aus der Scheide gezogen wird, und seine nahezu heilige Verbindung zu seinem Besitzer haben mehrere moderne Filme, Fernsehserien und Bücher inspiriert. In den Filmen Kill Bill I (2003) und Kill Bill II (2004) schwingt Uma Thurmans Figur „Die Braut“ ein Katana im heutigen Tokio, und in James Clavells klassischem Roman Shogun (1975) wird Captain James Blackthorne an der Küste Japans an Land gespült und von Samurai gefangen genommen.

Ein Foto eines Samurai, aufgenommen vom Fotografen Felice Beato, ca. 1860. Dieses Bild ist in den Vereinigten Staaten gemeinfrei, weil das Urheberrecht in Japan 1970 abgelaufen ist und vom Uruguay Round Agreements Act nicht wiederhergestellt wurde. Quelle: Britannica.
Seine Berühmtheit erlangte das Katana natürlich vor allem in der Hand seines Trägers. Doch wie stellten die japanischen Schwertschmiede diese Waffen für die Samurai her? Wie schufen sie das fein austarierte Gleichgewicht zwischen harten und weichen Teilen der Klinge, um das Katana einerseits rasiermesserscharf und andererseits biegsam genug für wiederholte Schläge zu machen? Warum ist die Klinge des Katana gebogen und nicht gerade? In diesem Blog-Beitrag werden wir zeigen, wie man den differentiellen Härtungsprozess eines Katanas modelliert, und seine Auswirkungen untersuchen, um einen Einblick in die Herstellung dieser historischen Waffe zu gewinnen.
Das Metal Processing Module
Das Metal Processing Module, ein Add-On zu COMSOL Multiphysics®, kann zur Modellierung von Phasenumwandlungen in Eisenlegierungen wie Stählen und in Titanlegierungen wie Ti-6Al-4V verwendet werden. Zu den Anwendungen gehören das Abschrecken von Stahl und die additive Fertigung. Mithilfe der Stahlabschreckung kann etwa das Härten von Getriebekomponenten für Kraftfahrzeuge modelliert werden, während bei der additiven Fertigung die wiederholten Kühl- und Heizzyklen, die beim Drucken auftreten, berücksichtigt werden können. Die Modellierungsfunktion für Phasenumwandlungen wird durch die Kopplung an Festkörpermechanik und Wärmetransport ergänzt, wodurch Effekte wie Plastizität und latente Wärme der Phasenumwandlung einbezogen werden können.
Differentialhärtung
Oft ist es erwünscht, nur Teile eines Bauteils zu härten. Ein Beispiel hierfür ist das Induktionshärten. Dabei wird mithilfe von elektrischen Spulen ein starkes magnetisches Wechselfeld angelegt, das an der Oberfläche des Bauteils elektrische Ströme induziert. Anschließend wird das Bauteil abgeschreckt und der Oberflächenbereich durchläuft eine martensitische Umwandlung. Dieses Verfahren der Differentialhärtung wird häufig bei Getriebeteilen wie Achsen und Zahnrädern eingesetzt, um die Verschleiß- und Dauerfestigkeit zu erhöhen.
Ein weiteres Verfahren zur Oberflächenhärtung von Bauteilen ist das Flammhärten. Anstelle eines magnetischen Wechselfeldes wird die Oberfläche durch Gasflammen lokal erwärmt und anschließend abgeschreckt.
Natürlich sind die Induktionshärtung und die Flammhärtung relativ neue Wärmebehandlungsverfahren, die japanischen Schwertschmieden vor vielen Jahrhunderten noch nicht zur Verfügung standen. Bei der traditionellen japanischen Katana-Herstellung wurde eine andere Art der Differentialhärtung verwendet. Bei einem Schwert dieser Art ist es von Vorteil, wenn die Schneide der Klinge hart ist – idealerweise rein martensitisch. Gleichzeitig ist der Klingenrücken vorzugsweise duktil, zum Beispiel perlitisch, da das Schwert sonst beim Aufprall brechen könnte. Die traditionelle Methode, ein Katana differentiell zu härten, besteht darin, die Klinge mit isolierendem Ton zu beschichten, um den Wärmetransport vom heißen Stahl zum umgebenden Wasser beim Eintauchen zu beeinflussen. Verschiedene Bereiche der Klinge werden mit unterschiedlich dickem Ton beschichtet. Im Bereich der Schneide wird eine dünnere Tonschicht aufgetragen als auf dem übrigen Teil der Klinge, wo eine dickere Schicht aufgetragen wird.
Die Multiphysik der Wärmebehandlung
Um die Wärmebehandlung eines Stahlbauteils zu simulieren, müssen Sie die für das Modell relevanten physikalischen Phänomene identifizieren.
Im Grunde wird der Prozess durch den Wärmetransport infolge des Wärmeaustauschs mit der Umgebung angetrieben. Die Temperaturänderung im Bauteil, in diesem Fall im Katana, induziert metallurgische Phasenumwandlungen (Zersetzung von Austenit in Ferrit, Perlit usw.). Bei Phasenumwandlungen wird latente Wärme erzeugt, die sich auf die Temperatur auswirkt. Die mit der Wärmeausdehnung und den Dichteunterschieden zwischen den Phasen verbundenen Volumenänderungen führen zu Verformungen des Bauteils sowie zu mechanischen Spannungen und plastischen Dehnungen. Es ist bekannt, dass Phasenumwandlungen unter mechanischer Beanspruchung zu unelastischen Dehnungen im Material führen, die als transformationsinduzierte Plastizität (TRIP) bezeichnet werden. Das Abschrecken ist ein echter multiphysikalischer Prozess, der dadurch erschwert wird, dass die einzelnen metallurgischen Phasen unterschiedliche Materialeigenschaften haben, die zu einem mittleren Verbundverhalten führen, das von der Phasenzusammensetzung abhängt.
Im vorliegenden Modell der Wärmebehandlung eines Katanas werden folgende Vereinfachungen vorgenommen:
- Latente Wärme bei Phasenumwandlungen wird vernachlässigt
- TRIP-Dehnungen werden vernachlässigt
Die Wärmebehandlung des Katanas ist in der folgenden Abbildung dargestellt.
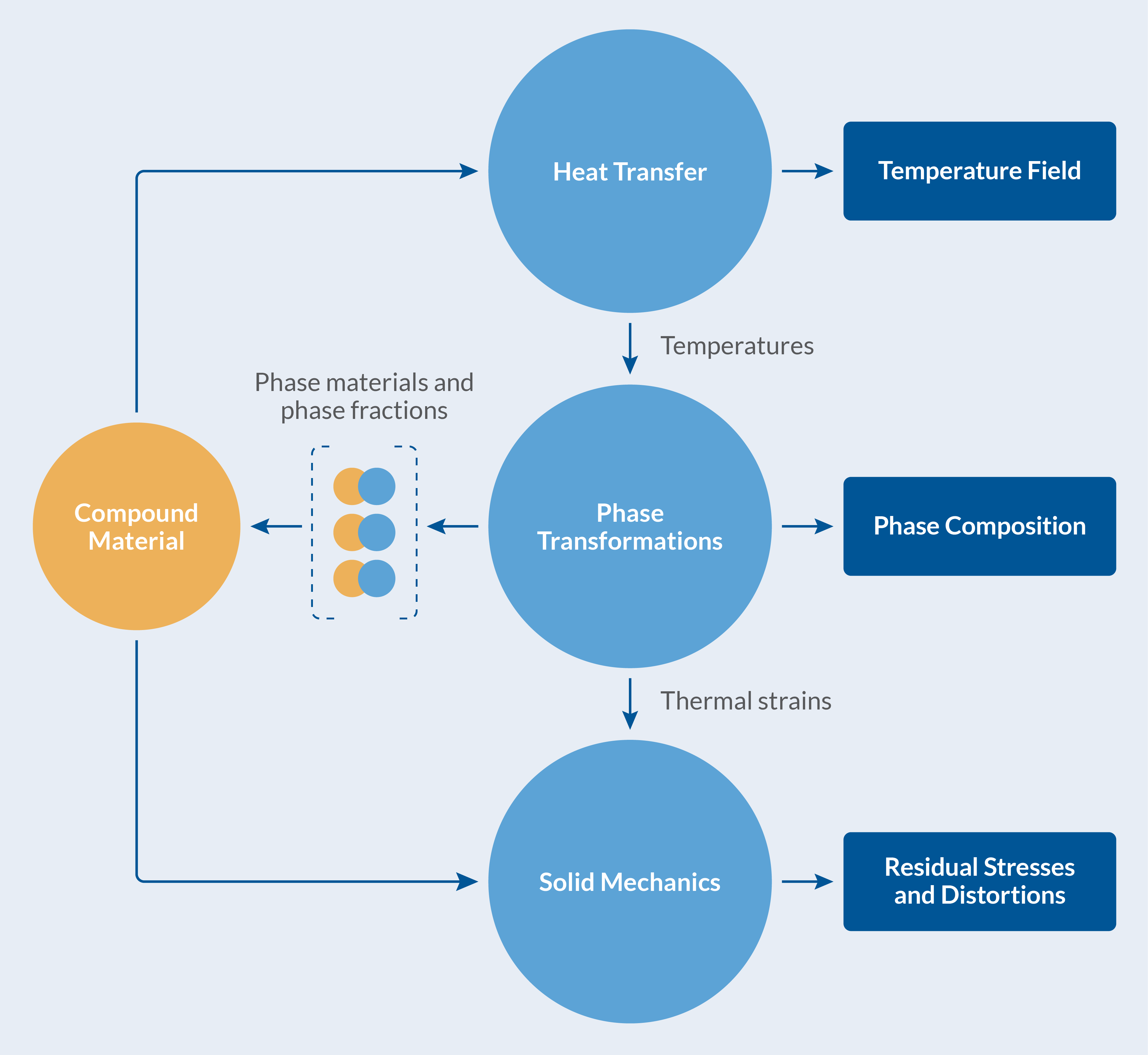 Die Multiphysik der Wärmebehandlung eines Katanas.
Die Multiphysik der Wärmebehandlung eines Katanas.
Das Material des Katanas
Bei der traditionellen Herstellung eines Katanas werden für die verschiedenen Bereiche der Klinge unterschiedliche Stahlsorten verwendet. In der Regel unterscheidet sich die Schneide vom Kern der Klinge, wobei der auffälligste Unterschied im unterschiedlichen Kohlenstoffgehalt liegt. Die Menge an Kohlenstoff und anderen Legierungselementen hat einen großen Einfluss auf die thermischen und mechanischen Eigenschaften des Stahls sowie auf die Phasenumwandlungseigenschaften. Hier wurde eine Vereinfachung auf eine einzige Stahlsorte vorgenommen. Der Legierungsgehalt ist in der folgenden Tabelle angegeben:
| Element | % des Gewichts |
|---|---|
| C | 0.63 |
| Mn | 0.9 |
| P | 0.04 |
In der Realität würde ein Stahl weitere Legierungselemente enthalten, aber der Einfachheit halber betrachten wir neben Kohlenstoff (C) nur Mangan (Mn) und Phosphor (P).
Geometrie des Katanas
Die Geometrie des Katanas: Die Klinge ist 50 cm lang (links) und der Querschnitt der Klinge ist 2,8 cm hoch (rechts).
Modellierung der Phasenumwandlung
Die verschiedenen möglichen Phasenumwandlungen müssen charakterisiert werden. Bei Raumtemperatur wird von einer Grundzusammensetzung des Stahls von 50 % Ferrit und 50 % Perlit ausgegangen. Das Katana wird zunächst erhitzt, bis diese Grundzusammensetzung vollständig in Austenit umgewandelt wurde. Anschließend wird das Katana in Wasser abgeschreckt, um die endgültige Phasenzusammensetzung zu erhalten. Diese Zusammensetzung variiert räumlich und besteht im Allgemeinen aus einer Kombination von Ferrit, Perlit, Bainit, Martensit und möglicherweise Restaustenit (siehe Abbildung). Die räumliche Variation wird durch die thermische Vorgeschichte an jedem Punkt des Materials während der Abkühlung beeinflusst.
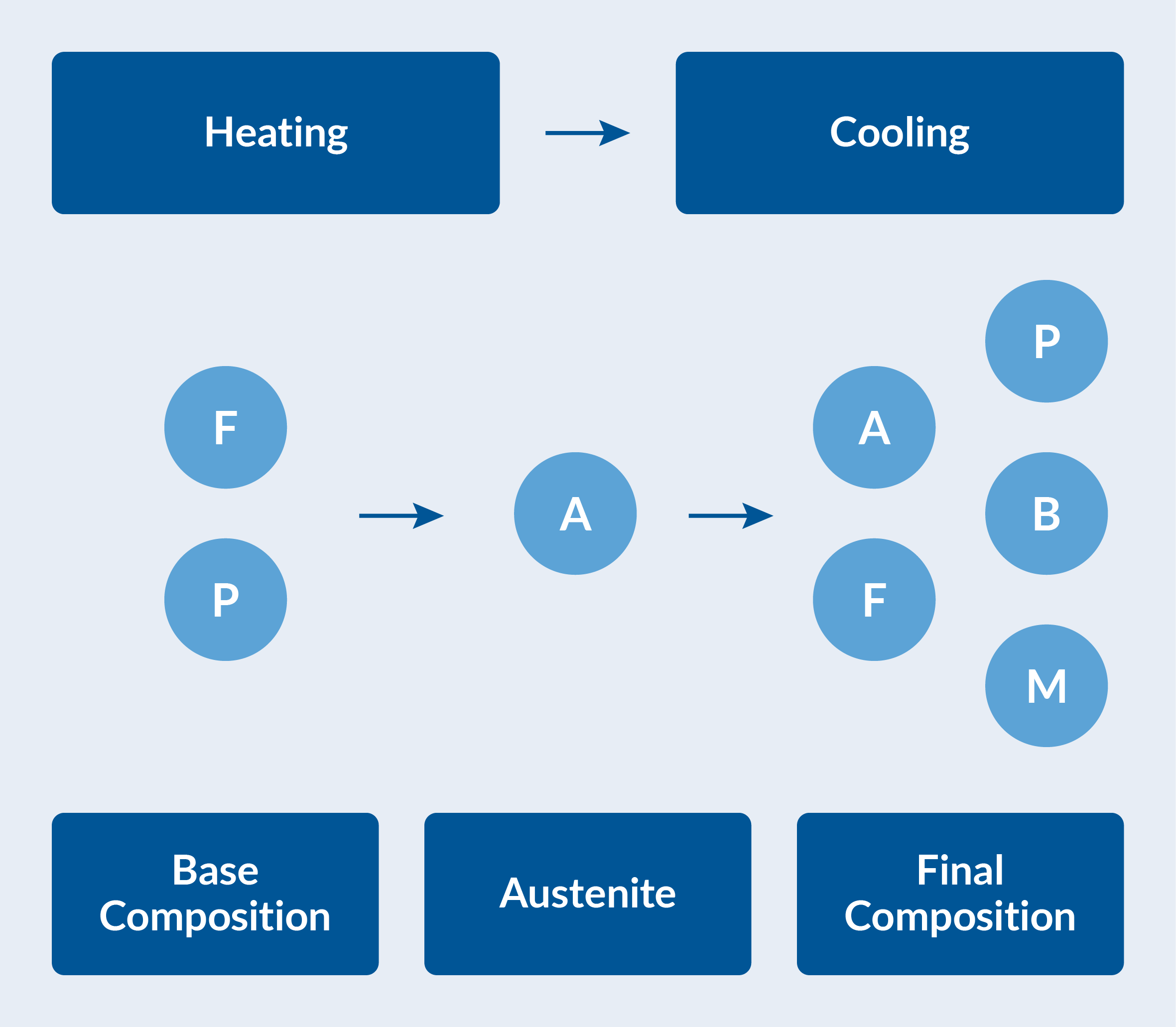
Phasenzusammensetzung beim Erhitzen und Abkühlen. Die Grundzusammensetzung von Ferrit (F) und Perlit (P) wandelt sich beim Erhitzen in Austenit (A) um. Der Austenit zerfällt beim Abkühlen in Ferrit, Perlit, Bainit (B) und Martensit (M).
Erwärmung
Die Simulation der Erwärmung dient nicht nur der Austenitisierung des ferritisch-perlitischen Stahls, sondern auch der Modellierung der thermischen Spannungen, die während der Erwärmung auftreten. Der Erwärmungsteil des Prozesses hätte auch weggelassen werden können, indem eine anfängliche Belastung zu Beginn der Abkühlung angewendet worden wäre, um den Effekt der thermischen Beanspruchung zu berücksichtigen. Wir haben uns dafür entschieden, die Erwärmung vor der Abkühlung zu modellieren. Da wir uns jedoch nicht mit der eigentlichen Austenitbildung befassen, verwenden wir das Phasenumwandlungsmodell von Leblond-Devaux, um die Austenitbildung aus der ferritisch-perlitischen Grundzusammensetzung zu modellieren. Das Phasenumwandlungsmodell verwendet einen Unterknoten Additional Source Phase, sodass sowohl Ferrit als auch Perlit als Ausgangsphasen für die Austenitbildung dienen. Die Raten der Phasenanteile von Austenit (A), Perlit (P) und Ferrit (F) werden dann wie folgt bestimmt:
wobei der Gleichgewichtsphasenanteil von Austenit eins ist (vollständige Austenitisierung) und die Zeitkonstante auf 60 Sekunden eingestellt ist:
Außerdem erlauben wir diese Phasenumwandlung nur während des Erwärmens, was durch den Unterknoten Transformation Condition mit der folgenden Bedingung c angegeben wird: audc.Tt>0.
Kühlung
Wenn das vollständig austenitische Katana in Wasser abgeschreckt wird, zerfällt der Austenit in eine Kombination aus Ferrit, Perlit, Bainit und Martensit. Je nach Abkühlungsgeschwindigkeit an verschiedenen Stellen der Klinge bilden sich Phasen in unterschiedlichen Mengen. Dies legt nahe, dass für die Abkühlung detailliertere Beschreibungen der Phasenumwandlungen erforderlich sind als für die Erwärmung. Die Zerlegung von Austenit in Ferrit, Perlit und Bainit wird daher mithilfe des Johnson-Mehl-Avrami-Kolmogorov-Modells (JMAK) der Phasenumwandlung modelliert. Dieses Modell eignet sich für die Modellierung von diffusen Phasenumwandlungen. Es hat drei Parameter:
- Der Anteil der Gleichgewichtsphase, \xi_\mathrm{eq}
- Die Zeitkonstante, \tau
- Der Avrami-Exponent, n
Der Gleichgewichtsphasenanteil stellt einen Gleichgewichtsphasenanteil der Zielphase dar, der als langfristige Asymptote betrachtet werden kann. So kann etwa der Anteil der Gleichgewichtsphase von Ferrit zwischen den Temperaturen A_{e1} und A_{e3} durch Anwendung der Hebelregel auf den Zweiphasenbereich von Austenit und Ferrit in einem Fe-C-Diagramm ermittelt werden. Um die übrigen Parameter zu bestimmen, können wir ein Zeit-Temperatur-Umwandlungsdiagramm (Time Temperature Transformation, TTT) verwenden. Ein TTT-Diagramm zeigt in der Regel, wann sich jede metallurgische Phase zu bilden beginnt und wann jede Umwandlung abgeschlossen ist. Es geht von isothermen Bedingungen aus, sodass bei der experimentellen Erstellung eines TTT-Diagramms eine Probe zunächst schnell auf eine „Zieltemperatur“ T_\mathrm{0} abgekühlt und dann auf dieser Temperatur gehalten werden sollte. Dieser Vorgang wird dann über einen bestimmten Temperaturbereich wiederholt, der üblicherweise von der Austenitisierungstemperatur bis zur Temperatur reicht, bei der sich Martensit bildet.
In der folgenden schematischen Darstellung zeigt die untere Hälfte ein TTT-Diagramm, dessen zwei Kurven die Zeiten angeben, die zur Bildung von 1 % und 99 % der Zielphase benötigt werden. Diese Anteile sind relative Phasenanteile, was bedeutet, dass sie bei jedem Temperaturniveau den Anteil der Zielphase im Verhältnis zu dem darstellen, was bei dieser Temperatur maximal erreichbar ist. Der relative Phasenanteil wird durch X =\xi^\mathrm{d}/\xi^\mathrm{d}_\mathrm{eq} angegeben, wobei der Gleichgewichtsphasenanteil im Allgemeinen temperaturabhängig ist. Wenn diese beiden TTT-Kurven experimentell ermittelt wurden, kann das JMAK-Phasenumwandlungsmodell bei jeder Temperatur genau angepasst werden. Die dazwischenliegenden relativen Phasenanteile werden dann durch die Formulierung des JMAK-Modells selbst bestimmt. Die obere Hälfte des Schemas zeigt die Entwicklung der Zielphase, wie sie durch ein bestimmtes Phasenumwandlungsmodell bei T=T_0 bestimmt wird.
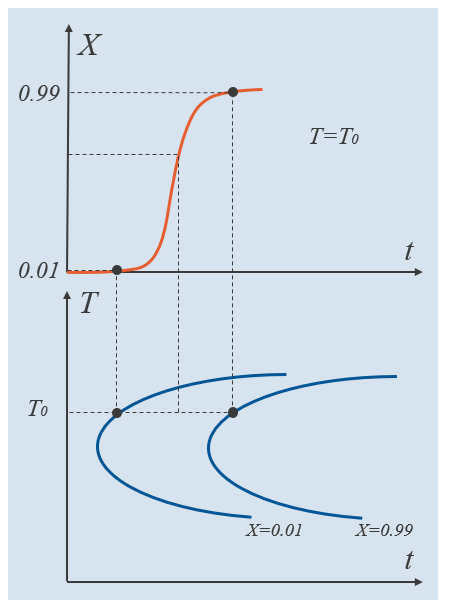
Beispiel für TTT-Kurven für die relativen Phasenanteile 0,01 und 0,99. Ein dazwischenliegender relativer Phasenanteil ist angegeben.
In COMSOL Multiphysics® wird das JMAK-Phasenumwandlungsmodell in Ratenform ausgedrückt, wodurch es für nicht-isotherme Bedingungen geeignet ist. Im Sinne der TTT-Analyse können wir das JMAK-Modell jedoch symbolisch integrieren. Die Entwicklung der Zielphase mit der Zeit wird zu:
Nach einigen Umformungen kann diese Gleichung wie folgt ausgedrückt werden:
Wenn wir die Start- und Endzeiten und Phasenanteile aus der obigen Abbildung verwenden und davon ausgehen, dass der Gleichgewichtsphasenanteil bekannt ist, können wir den Avrami-Exponenten n und die Zeitkonstante \tau ermitteln:
Genau dies geschieht bei der Formulierung der TTT-Diagrammdaten für das JMAK-Phasentransformationsmodell im Knoten Phase Transformation.
Im aktuellen Abschreckmodell des Katanas werden drei fiktive, aber realistische Reihen von Start- und Endkurven der TTT verwendet, um die Zersetzung von Austenit in Ferrit, Perlit bzw. Bainit zu definieren. Für Ferrit lautet ein Abschnitt der Daten:
| T \, (^{\circ}C) | t_1 \, (s) | t_{99} \, (s) |
|---|---|---|
| 575 | 2.2 | 43 |
| 580 | 0.22 | 2.1 |
| 585 | 0.075 | 1.42 |
| 590 | 0.076 | 1.47 |
| 595 | 0.078 | 1.47 |
| 600 | 0.079 | 1.49 |
| 605 | 0.081 | 1.54 |
| 610 | 0.084 | 1.58 |
| 615 | 0.086 | 1.63 |
| 620 | 0.090 | 1.70 |
| \vdots | \vdots | \vdots |
| \vdots | \vdots | \vdots |
| 730 | 5.8 | 110 |
| 735 | 13 | 254 |
| 740 | 41 | 820 |
| 745 | 322 | 6246 |
Um die Definitionen des Phasenumwandlungsmodells zu vervollständigen, müssen wir außerdem Folgendes ermitteln:
- Die temperaturabhängigen Gleichgewichtsphasenanteile für Ferrit, Perlit und Bainit für die jeweiligen Phasenumwandlungen.
- Die oberen und unteren Temperaturgrenzen für die Phasenumwandlung. Beispielsweise definiert A_\mathrm{e3} den Beginn der ferritischen Umwandlung und M_\mathrm{s} ist die Martensitstarttemperatur.
Die Gleichgewichtsphasenanteile und die verschiedenen Umwandlungstemperaturen werden auf der Grundlage der chemischen Zusammensetzung unter Verwendung des Knotens Steel Composition unter dem Interface Austenite Decomposition berechnet.
Wir lassen diese Phasenumwandlungen nur während des Abkühlens zu und steuern dies genau wie beim Erwärmen über den Unterknoten Transformation Condition, in den die folgende Bedingung c eingegeben wird: audc.Tt<=0.
Wenn die TTT-Kurven für die Phasenumwandlung in Ferrit, Perlit und Bainit zusammen verwendet werden, kann mithilfe des Interfaces Austenite Decomposition ein TTT-Diagramm berechnet werden. Die folgende Abbildung zeigt das berechnete TTT-Diagramm. Zur Modellierung wird das Interface Austenite Decomposition in 0-D verwendet und die Zeiten zum Erreichen bestimmter Phasenanteile werden durch Auswahl von Compute transformation times in den Phasenknoten ermittelt.
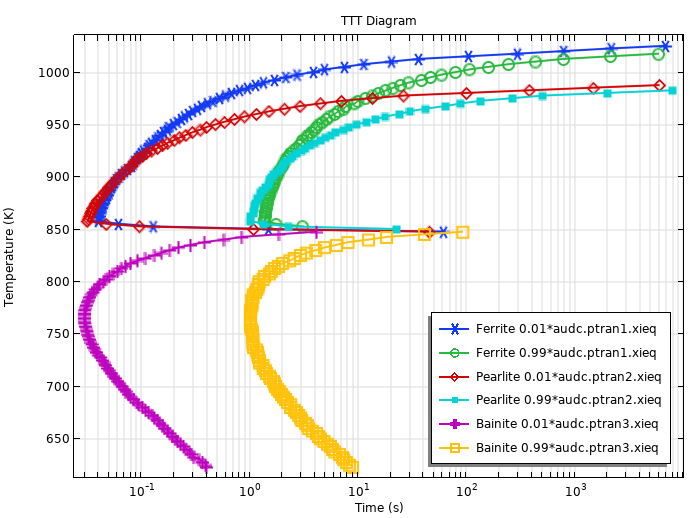
Berechnetes TTT-Diagramm unter Verwendung der fiktiven TTT-Daten.
Die martensitische Phasenumwandlung wird durch das Phasenumwandlungsmodell von Koistinen-Marburger beschrieben. Dieses Modell erfordert zwei Parameter:
- Der Koistinen-Marburger-Koeffizient, \beta
- Die Martensitstarttemperatur, M_\mathrm{s}
Im Gegensatz zu den diffusen ferritischen, perlitischen und bainitischen Umwandlungen, die unter isothermen Bedingungen betrachtet wurden, ist die martensitische Umwandlung von Natur aus temperaturratenabhängig. Die Geschwindigkeit, mit der sich Martensit bildet, ist nach dem Modell von Koistinen-Marburger proportional zur Abkühlgeschwindigkeit durch den Koeffizienten \beta.
Da alle Phasenumwandlungen definiert sind, kann auch ein Diagramm der kontinuierlichen Abkühlung (Continuous Cooling Transformation, CCT) berechnet werden. Die folgende Abbildung zeigt ein CCT-Diagramm, bei dem die Austenitisierungstemperatur 900 °C beträgt und die Abkühlraten zwischen 0,1 K/s und 1000 K/s liegen. Die 1%-Linien für die gebildeten Phasen Ferrit, Perlit, Bainit und Martensit sind eingezeichnet. Auch für den Austenit ist die 1%-Linie dargestellt. Der Zerfall von fast dem gesamten Austenit in andere Phasen wird als Abschluss der Austenitzersetzung betrachtet.
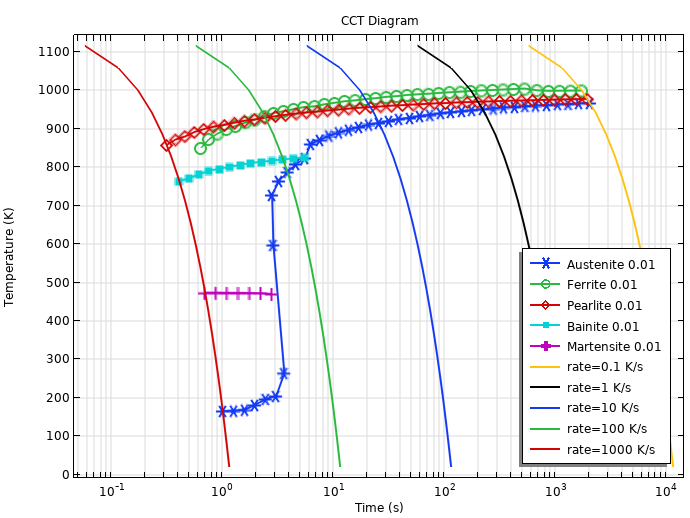
Berechnetes CCT-Diagramm basierend auf den TTT-Daten.
Mechanische und thermische Materialeigenschaften
Für ein detailliertes Abschreckmodell eines Stahlbauteils wie eines Katanas werden thermische und mechanische Eigenschaften benötigt. Diese temperaturabhängigen Eigenschaften variieren zwischen Phasen wie Austenit und Ferrit. Elastoplastische Eigenschaften sind im Allgemeinen auch von der Dehnung und möglicherweise von der Dehnrate abhängig. Die experimentelle Ermittlung einer vollständigen Reihe von Materialeigenschaften ist zeitaufwendig und kostspielig und daher oft unerschwinglich. In der Praxis werden andere Quellen verwendet, wie experimentelle Daten aus der Literatur und berechnete Materialeigenschaften. Der Zweck der vorliegenden Simulation besteht darin, das Abschrecken eines Katanas zu demonstrieren, und vor diesem Hintergrund nehmen wir die folgenden Modellierungsvereinfachungen vor:
- Die elastischen Eigenschaften werden von den Phasen geteilt, die übrigen Eigenschaften werden als zwischen den Phasen variierend angenommen.
- Die Wärmeleitfähigkeiten und die Wärmekapazitäten werden als temperaturabhängig angenommen.
- Die anfänglichen Fließspannungen werden als temperaturabhängig angenommen.
- Das Härtungsverhalten der Phasen wird als linear und isotrop sowie temperaturabhängig angenommen.
- Die Wärmeausdehnungskoeffizienten sind konstant, die Bezugsvolumentemperaturen variieren.
Die Materialeigenschaften jeder Phase werden zusammen mit der sich entwickelnden Phasenzusammensetzung (Phasenanteile) zur Berechnung der effektiven Materialeigenschaften verwendet. Dies erfolgt automatisch im Metal Processing Module, und die berechneten effektiven Eigenschaften werden in einem Compound Material gesammelt, damit sie in anderen Physik-Interfaces transparent genutzt werden können. Die folgende Abbildung veranschaulicht dies.
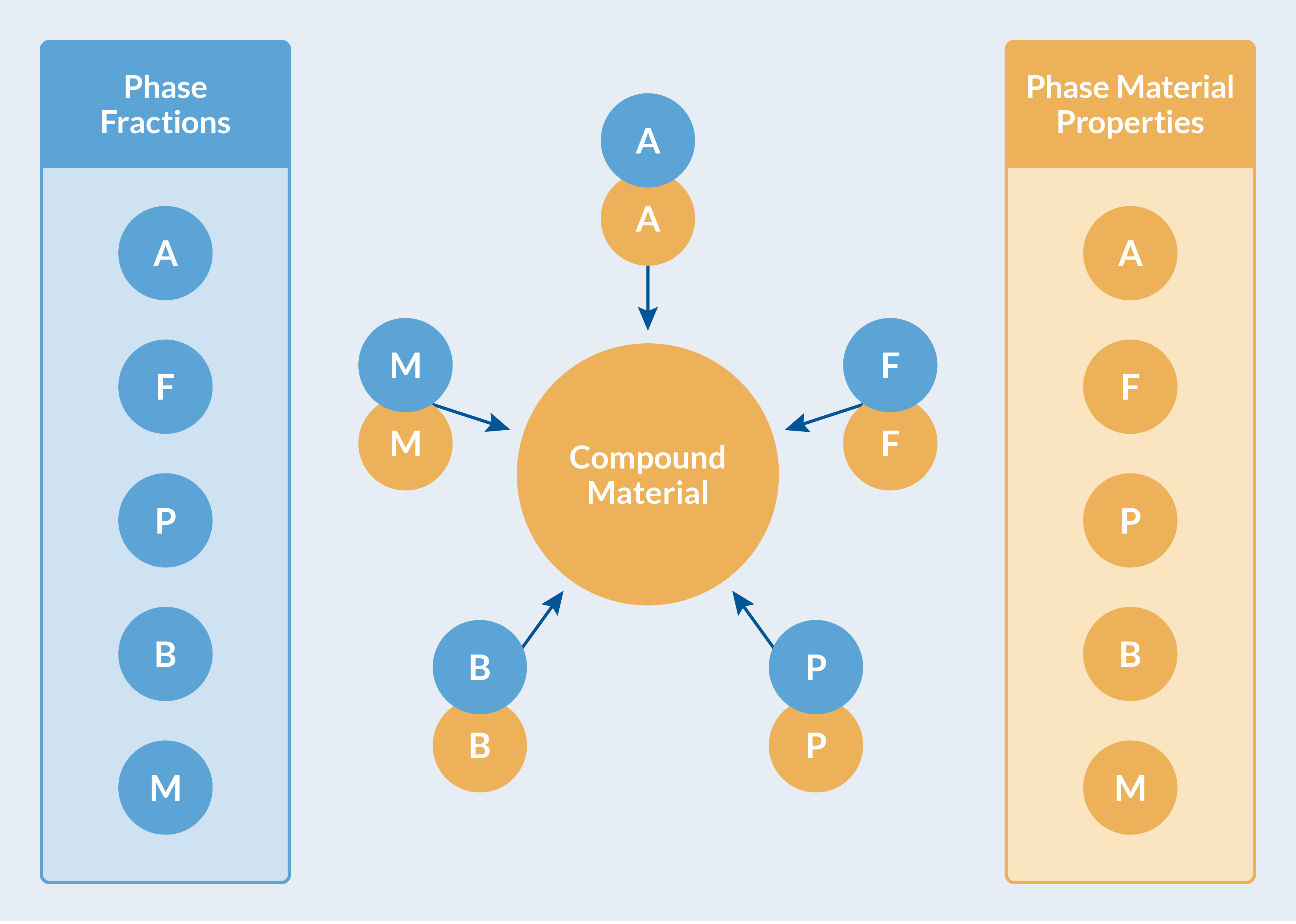
Die berechneten effektiven Materialeigenschaften werden in einem Compound Material zusammengetragen.
Modellierung des Wärmetransports
Das Interface Heat Transfer in Solids wird verwendet, um den Wärmetransport im Katana und den Wärmeaustausch mit der Umgebung zu modellieren. Der Einfachheit halber wird die Strahlung vernachlässigt und der Wärmetransport von der Klinge zur Umgebung ausschließlich durch Konvektion modelliert. Auf der Oberfläche der Klinge wird ein Wärmestrom vorgeschrieben, der durch einen temperaturabhängigen Wärmeübergangskoeffizienten charakterisiert ist.
Erwärmung
Das Katana wird erhitzt, um die ferritisch-perlitische Grundzusammensetzung austenitisieren zu lassen. Zur Modellierung verwenden wir ein vereinfachtes Konvektionsmodell mit einem konstanten Wärmeübergangskoeffizienten von 300 W/m^2K. Die Umgebungstemperatur wird während der ersten Minute der Erwärmung von Raumtemperatur auf 850 °C erhöht und dann für die Dauer der Erwärmung konstant gehalten. Die Gesamtzeit wird so gewählt, dass sich das Material vollständig in Austenit umwandelt, und die Erwärmung erfolgt so, dass die Temperaturgradienten im Katana gering genug sind, um thermisch induzierte plastische Dehnungen zu vermeiden.
Kühlung
Um die Auswirkungen unterschiedlicher Dicken des Isoliertons nachzuahmen, wird sich der Wärmeübergangskoeffizient für den Bereich nahe der Klingenschneide von dem für den oberen Teil der Klinge unterscheiden.
Die folgende Abbildung zeigt die temperaturabhängigen Wärmeübergangskoeffizienten, die zur Darstellung dünner und dickerer Tonschichten verwendet wurden.
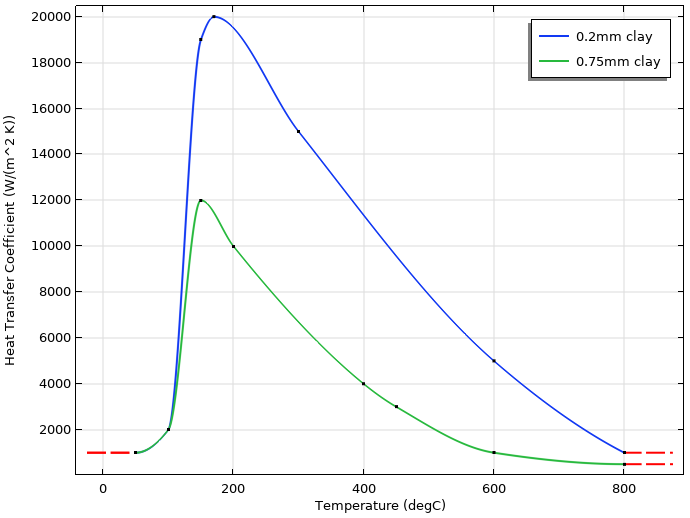
Temperaturabhängige Wärmeübergangskoeffizienten für die dünne (0,2 mm) und dickere (0,75 mm) Tonschicht. Die dünne Schicht wird auf die Schneide aufgetragen, die dickere Schicht auf den Rest der Klinge.
Modellierung von Spannungen und Dehnungen
Das Interface Solid Mechanics wird zur Berechnung von Spannungen, Dehnungen und Verzerrungen des Katanas während des thermischen Übergangs verwendet. Wir haben bereits darauf hingewiesen, dass thermische Ausdehnungs- und Dichteunterschiede zwischen den Phasen zu Verzerrungen des Bauteils sowie zu mechanischen Spannungen und plastischen Dehnungen führen. Diese Effekte werden vom Interface Austenite Decomposition verarbeitet und über die Multiphysik-Kopplung Phase Transformation Strain an das Interface Solid Mechanics übertragen. Wir rechnen mit einer erhebliche Biegung des Katanas, was bei einer schlanken Struktur wie dieser nicht unbedingt zu großen Materialdehnungen führt. Allerdings sind endliche Rotationen beteiligt, sodass die Analyse geometrisch nichtlinear ist. Außerdem wird erwartet, dass die Biegung plastische Dehnungen verursacht, was durch den Unterknoten Plasticity unter Linear Elastic Material berücksichtigt wird.
Ergebnisse
Eines der auffälligsten Merkmale des Katanas ist seine gebogene Klinge. Interessanterweise entsteht diese Krümmung durch den Härtungsprozess und nicht durch das Biegen der Klinge vor der Wärmebehandlung. Da die Klinge zur Schneide hin dünner ist und der isolierende Ton dort dünner aufgetragen wird, sinkt die Temperatur schnell ab. Wenn der Austenit abkühlt und sich zusammenzieht, biegt sich die Klinge daher zunächst nach unten. Mit dem Absinken der Temperatur unter die Martensitstarttemperatur beginnt die Umwandlung des Austenits in Martensit. Die Umwandlung in Martensit ist mit einer Volumenausdehnung verbunden, die zu Druckspannungen an der Schneide führt. Mit fortschreitender Abkühlung in Richtung Klingenrücken verlangsamt sich die Abkühlgeschwindigkeit und es bilden sich andere metallurgische Phasen. Die anfängliche Abwärtskrümmung der Klinge geht in die endgültige, traditionell gekrümmte Form über. Die untere Abbildung zeigt die endgültige Zusammensetzung der metallurgischen Phasen. Auffällig ist, dass die Schneide martensitisch und damit hart ist, während der Klingenrücken überwiegend perlitisch und damit deutlich duktiler ist.
Phasenanteil von Martensit (oben), axiale Spannung (Mitte) und Temperatur (unten) während des Abkühlens.
Die endgültige Zusammensetzung nach dem Abschrecken. Die Kante weist die gewünschte harte martensitische Struktur auf und der Klingenrücken ist größtenteils perlitisch.
Anwendung
In diesem Blog-Beitrag haben wir gezeigt, wie man das Abschrecken eines Katanas mit COMSOL Multiphysics® simulieren kann. Wir haben erklärt, wie das Katana seine geschwungene Form erhielt und wie eine vereinfachte Version des traditionellen Verfahrens, bei dem Ton für das differentielle Härten verwendet wurde, eine Klinge mit einer harten Schneide und einem weichen Kern erzeugte. Natürlich ist die Modellierung eines Katanas aus reiner Neugierde entstanden, aber sie hat gezeigt, dass COMSOL Multiphysics® für allgemeine Simulationen der Stahlhärtung verwendet werden kann, mit denen man nicht nur die Zusammensetzung metallurgischer Phasen berechnen, sondern auch Verformungen und Restspannungen vorhersagen kann.
Probieren Sie es selbst aus
Möchten Sie die differentielle Härtung eines Katanas modellieren? Die Modelldateien sind in der Application Gallery verfügbar.





Kommentare (0)