In mikrofluidischen Systemen ist die Strömung immer laminar. Dies ist sowohl ein Vorteil als auch ein Nachteil – ein Vorteil, weil das Strömungsfeld stationär ist, und ein Nachteil, weil die Vermischung der Spezies hauptsächlich durch Diffusion erfolgt, was zeitaufwendig sein kann. Eine einfache Möglichkeit, chemische Spezies in einem mikrofluidischen Chip zu mischen, ist die Verwendung einer serpentinenförmigen Kanalstruktur. Mit der Software COMSOL Multiphysics® kann die Periodizität einer solchen Struktur genutzt werden, um die erforderliche Kanallänge zu bestimmen, die sicherstellt, dass die chemischen Spezies das System gut vermischt verlassen.
Modellierung periodischer mikrofluidischer Systeme mit COMSOL Multiphysics®
Ein Beispiel für ein mikrofluidisches System mit Serpentinenkanälen ist in der folgenden Abbildung dargestellt. Verdünnte Lösungen chemischer Spezies können über die beiden Einlässe in das System gelangen. Die Fluide fließen zusammen und durch die Serpentinenkanäle. Da die Strömung in mikrofluidischen Systemen laminar ist, erfolgt die Vermischung der chemischen Spezies durch Diffusion. Für die Erstellung einer effizienten Simulation können wir die periodische Struktur nutzen und eine einzelne sich wiederholende Einheitszelle betrachten.
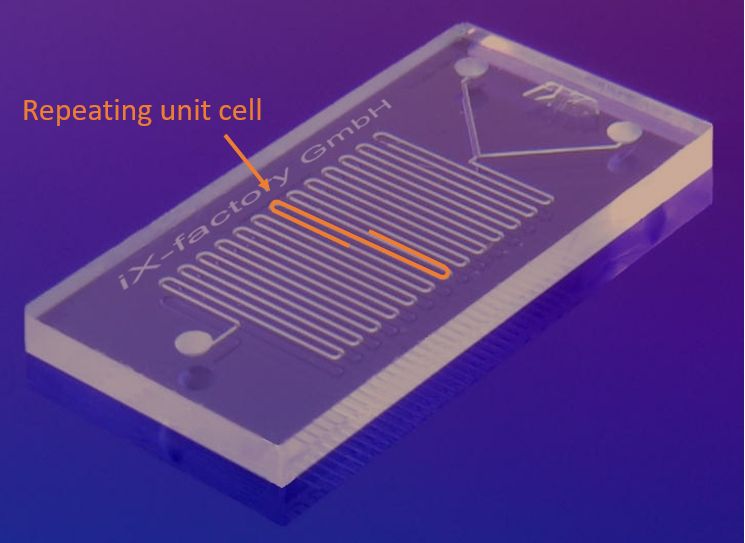
Ein typisches mikrofluidisches System. Das Bild wurde bearbeitet. Originalbild von IX-factory STK – eigenes Werk, lizenziert unter CC BY-SA 3.0 über Wikimedia Commons. Das Original wurde modifiziert.
Der hier vorgestellte Serpentinenkanal wurde auch in zwei früheren Blog-Beiträgen behandelt. In dem im ersten dieser Blog-Beiträge diskutierten Ansatz zur Verwendung von Extrusionsoperatoren für die Modellierung periodischer Strukturen wird die laminare Strömung für eine sich wiederholende Einheitszelle berechnet, wodurch die Rechenlast reduziert wird. Das Geschwindigkeitsfeld wird dann mithilfe des Operators General Extrusion auf die vollständige Geometrie abgebildet, die mehrere sich wiederholende Einheitszellen enthält. Mit dem abgebildeten Geschwindigkeitsfeld wird der Transport verdünnter Spezies auf der vollständigen Geometrie gelöst, wie in der folgenden Abbildung dargestellt.
Der erste Modellierungsansatz zur Simulation eines periodischen mikrofluidischen Systems. Das Geschwindigkeitsfeld wird in einer Einheitszelle simuliert und auf die gesamte Geometrie abgebildet. Das Konzentrationsprofil wird für die gesamte Geometrie berechnet.
Im zweiten Blog-Beitrag zur Ausnutzung der Periodizität in Modellen mit hohen Péclet-Zahlen wird das Modell weiter vereinfacht. Der Schwerpunkt liegt auf mikrofluidischen Systemen mit einer hohen Péclet-Zahl. Der Stofftransport wird mehr durch Advektion als durch Diffusion bestimmt, folglich hat die stromabwärts befindliche Lösung keinen Einfluss auf die stromaufwärts befindliche Lösung. Daher ist es nicht notwendig, den Stofftransport im gesamten System zu berechnen, wie es beim ersten Ansatz der Fall ist.
Bei hohen Péclet-Zahlen kann der Speziestransport daher sequenziell berechnet werden, eine Einheitszelle nach der anderen. Dazu wird das Geschwindigkeitsfeld in einer Einheitszelle berechnet, wie in der folgenden Abbildung dargestellt („Methode 2“). Anschließend wird das Konzentrationsfeld in einer Einheitszelle berechnet. Mit dem Feature General Extrusion wird das Konzentrationsfeld am Auslass auf den Einlass zurückgemappt. Um sicherzustellen, dass die vorherige Lösung für das Konzentrations-Mapping in der nächsten Iteration verwendet wird, werden das Interface Boundary ODEs and DAEs und das Feature Previous Solution verwendet.
In diesem Blog-Beitrag stellen wir einen anderen Weg vor, um dasselbe Ziel zu erreichen: die Übertragung der Ergebnisse vom Auslass zurück zum Einlass für die sequentielle Berechnung des Speziestransports. Anstelle einer gewöhnlichen Differentialgleichung am Rand verwenden wir eine Zustandsvariable. Die Zustandsvariable ist einfacher zu implementieren als die gewöhnliche Differentialgleichung, wodurch die Komplexität des Modells reduziert wird.
Der zweite und dritte Modellierungsansatz zur Simulation eines periodischen mikrofluidischen Systems unter Verwendung nur einer einzelnen Einheitszelle. Die Methoden unterscheiden sich in Schritt 3. Die Abbildung des Konzentrationsprofils vom Auslass zum Einlass der nächsten Einheitszelle kann entweder mithilfe einer gewöhnlichen Differentialgleichung oder einer Zustandsvariablen implementiert werden. (Der letztere Ansatz wird unten erläutert.)
General Extrusion und eine Zustandsvariable
Die Modellierung beginnt mit der Definition des Operators General Extrusion, genext1. Der Operator befindet sich unter Definition Nonlocal Couplings. Dieser Operator ist am Rand des Auslasses definiert und bildet aufgrund der angegebenen Verschiebung einen Ausdruck – in diesem Fall die Konzentration – vom Auslass zum Einlass in x ab.
Der Operator General Extrusion bildet eine Variable von einem Rand zum anderen durch einen Versatz von 6 mm in x-Richtung ab.
Im zweiten Schritt wird die Zustandsvariable am Einlassrand definiert. Das entsprechende Feature State Variables finden Sie unter Definitions > Variable Utilities. Zustandsvariablen werden im Modell als abhängige Variablen behandelt. Im Gegensatz zu den üblichen abhängigen Variablen in einem Physik-Interface können Zustandsvariablen so eingestellt werden, dass sie vor oder nach jedem konvergierten Parameter- oder Zeitschritt oder nur bei der Initialisierung aktualisiert werden. Die Einstellungen für die Zustandsvariable sind in der folgenden Abbildung dargestellt. Die Zustandsvariable wird c_b genannt und eine Stufenfunktion wird als Anfangswert verwendet, um den anfänglichen Konzentrationsgradienten am Einlass darzustellen. Die Stufenfunktion befindet sich bei x = 0,5 mm und die Anfangskonzentration variiert je nach x-Position zwischen 0 und 1 mol/m3. Die Zustandsvariable wird immer zu Beginn eines Parameterschritts aktualisiert. Das bedeutet, dass die Konzentration am Auslass des vorherigen Schritts für die nächste Iteration auf den Einlass abgebildet wird.
Das Fenster Settings für die Zustandsvariable.
Die Zustandsvariable c_b wird als Konzentration am Rand Inflow im Interface Transport of Diluted Species verwendet. Die Daten der Zustandsvariablen werden an Gauß-Punkten und nicht an Knotenpunkten gespeichert. Aus diesem Grund wählen wir als Boundary Condition Type Flux (Danckwerts) anstelle von Concentration constraint. Die Konzentrationsbedingung wird auf die Knotenpunkte angewendet, während die Danckwerts-Bedingung einen Fluss an den Gauß-Punkten vorgibt.
Die Zustandsvariable c_b wird als Konzentration am Rand des Einlasses festgelegt.
Um einen Extrapolationsfehler zu minimieren, wird das Feature Identical Mesh an den Rändern der Ein- und Auslässe verwendet.
Das Einstellungsfenster für das Feature Identical Mesh. Die Ränder 2 und 7 sind der Einlass- bzw. Auslassrand.
Ähnlich wie im vorherigen Blog-Beitrag berechnen wir das Modell in zwei Schritten. Die Einstellungen für die Studienschritte sind in der folgenden Abbildung dargestellt. Im ersten Studienschritt wird nur das Interface Laminar Flow für eine Einheitszelle berechnet. Das Strömungsfeld ist dasselbe, unabhängig davon, wie viele Wiederholungen der Einheitszelle berücksichtigt werden. Dies ist beim Speziestransport nicht der Fall. Im zweiten Schritt werden der Transport verdünnter Spezies und die Zustandsvariable berechnet. Zusätzlich führen wir einen Parameter n_unit_cells für die sequenzielle Berechnung der sich wiederholenden Einheitszellen ein. Dieser Parameter wird im Auxiliary Sweep verwendet und von 1 in Schritten von 1 bis zur maximalen Anzahl von Einheitszellen, in diesem Fall 15, gesweept. Am Ende jeder Berechnung wird die Zustandsvariable aktualisiert und das Konzentrationsfeld des Auslasses wird auf den Einlass für die nachfolgende Einheitszelle abgebildet. Die Einstellung Run continuation for ist auf No parameter und Reuse solution from previous step auf Yes gesetzt, um die Zustandsvariable korrekt zu aktualisieren.
Die Einstellungen für den Studienschritt mit dem aktivierten Feature Auxiliary Sweep. Der Parameter n_unit_cells steht für die Anzahl der Einheitszellen.
Als Ergebnis erhalten wir das Konzentrationsprofil über alle Wiederholungen der Einheitszellen. In der folgenden Abbildung sind die ersten drei Einheitszellen dargestellt.
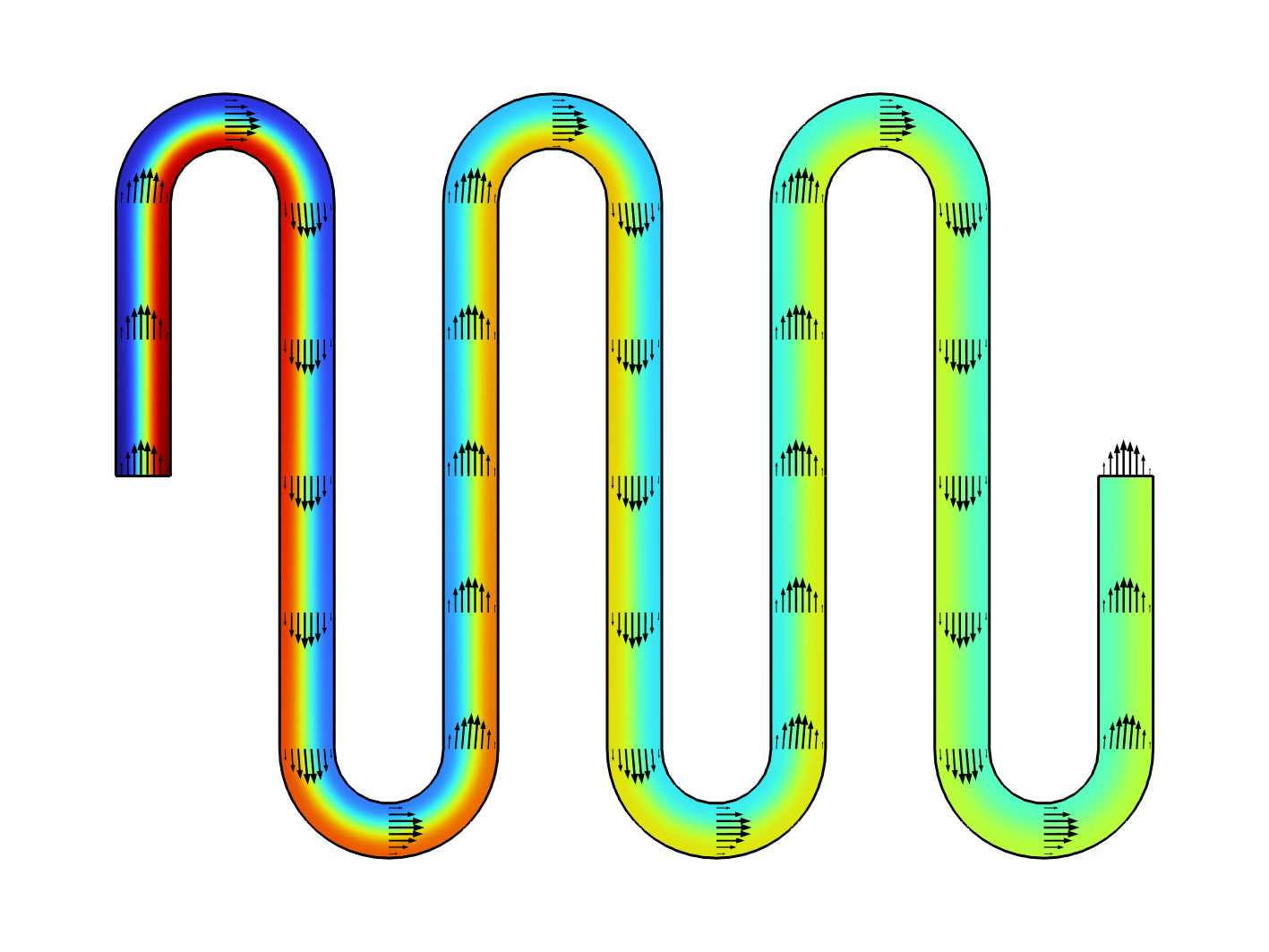
Konzentrationsprofil der ersten drei Einheitszellen.
Die hier vorgestellten Simulationsergebnisse können zur Bestimmung des Mischungsgrads und der erforderlichen Kanallänge verwendet werden. Der effiziente Ansatz der Verwendung des Auxiliary Sweep ermöglicht es uns, den Mischer nach Belieben zu vergrößern. Um zu messen, wie gut ein System gemischt ist, können wir den Mischungsindex (MI) betrachten. Der Mischungsindex wird über den Kanalquerschnitt berechnet und ist wie folgt definiert:
wobei \textless{c}\textgreater die durchschnittliche Konzentration am Auslassrand und {\sigma} ihre Standardabweichung ist.
Der Mischungsindex als Funktion der Anzahl der Einheitszellen.
Der Plot zeigt den Mischungsindex am Auslass jeder Einheitszelle für 15 Wiederholungen. Ein Mischungsindex von 0,98 wird bereits nach 5 Einheitszellen erreicht.
Die wichtigsten Erkenntnisse
Die hier gezeigte Methode ähnelt stark der in unserem Blog-Beitrag Exploiting Periodicity in Models with High Péclet Numbers beschriebenen. Diese Methoden vereinfachen das Modell und sparen Rechenressourcen. Der Hauptunterschied zur vorherigen Methode besteht darin, dass anstelle einer gewöhnlichen Differentialgleichung eine Zustandsvariable verwendet wird, um die Ausgangskonzentration zu speichern und an die nächste Iteration zu übertragen. Die Methode mit der Zustandsvariablen ist einfacher zu implementieren, da sie keine Änderungen in den Löserkonfigurationen erfordert. Daher empfehlen wir die Verwendung der Zustandsvariablenmethode zur Modellierung von Systemen mit einer hohen Péclet-Zahl. Dieser Ansatz kann auch auf komplexere Anwendungen angewendet werden, wie zum Beispiel das Mischen mehrerer chemischer Spezies, die zu anderen Spezies reagieren.
Weitere Ressourcen
Möchten Sie mehr über einige der hier erwähnten Features erfahren? Dann lesen Sie diese Blog-Beiträge:
- Lernen Sie, wie Sie mit Gauß-Punkten arbeiten: “Introduction to Numerical Integration and Gauss Points”
- Lernen Sie mehr über das Feature State Variables: “How to Use State Variables in COMSOL Multiphysics®”
- Lernen Sie, wie Sie den Operator General Extrusion nutzen können: “Mapping Variables with General Extrusion Operators”
- Lernen Sie mehr über die Verwendung des Operators General Extrusion: “Examples of the General Extrusion Operator”
Kommentare (0)