Veröffentlichungen und Präsentationen

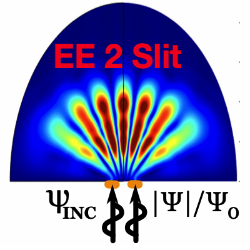
INTRODUCTION: The paper illustrates the use of COMSOL for obtaining the solution Ψ(x,y,t) as a solution to the time dependent nonlinear Schrödinger equation (NLSE). COMSOL previously was used to solve the time dependent NLSE in Ref.[1] as applied to quantum mechanics, however this is the first application of NLSE to water surface waves. The governing fluid mechanics PDEs in terms of the primary variables surface elevation of water h(x,y,t) and velocity potential φ'(x,y,t) are transformed into an alternate form of two simultaneous coupled PDEs having the form of the NLSE, where now the complex wave amplitude Ψ(x,y,t) (called wave function in quantum mechanics) and associated potential Φ become the new transformed unknowns. USE OF COMSOL MULTIPHYSICS: Nonstandard PDE’s often encountered in physics research is a good fit for applying COMSOL’s general equation solving capabilities. The Equation Based Modeling General-Form PDE "time dependent" study is employed herein. The distortion of the freely propagating Schrödinger equation waves by the presence of a nonlinear Ψ|Ψ|^2 term in the nonlinear Schrödinger equation is examined through a series of examples by varying the PDE parameters which govern which class of PDEs these represent (e.g. Elliptic-Elliptic(EE), Elliptic-Hyperbolic(EH), or Hyperbolic-Elliptic (HE). RESULTS: A series of increasing complex models are examined starting with simple Free Field PW propagating down a wave guide for each of the EE, EH and HE category cases. Figure 1 is an example of the EE case and shows two time snapshots of the normalized |Ψ′| vs x′ both with the nonlinear term Ψ|Ψ|^2 in play vs linearizing it with Ψ|Ψ|^2 -> Ψ. Figure 2 is the same solution but vs. normalized time t′ at two fixed x′ locations. Solution validation is made by solving the same problem with an alternate FEM application (labeled as Math) where good agreement is achieved. With the same model parameters employed in the 1D examples, 2D models are examined by driving the field through 1 slit as in Fig.3 and then through 2 slits as in Fig.4 . The 1D Fig.1a repeated string of spikes is also similar to the 2D Fig.3a radial string of spikes formation. The Fig.4 build up of constructive and destructive interference patterns are formed as the two sources interact. In the paper the effect of varying controlling model parameters such as those defining the EE, EH and HE PDE class , nonlinear-linear PDE coefficient, and temporal drivers (steady wave train vs short pulse ) are evaluated . CONCLUSION: The application of COMSOL to pure physics is explored and successfully applied, with particular emphasis on solving nonlinear partial differential equations. Validation checking against alternative FEM solutions showed good comparisons. The dramatic effect of the nonlinear term in the DS equations gives insight on how rough surface waves are formed.