Supplement B: More Information on Iterative Solvers for 3D Analysis
For 3D models, a suggested predefined iterative solver is included in the default-generated solver settings. Depending on your modeling requirements, it may be necessary to use and/or adjust an iterative solver. The information included in an iterative solver can help to efficiently solve your models.
Background on the Autogenerated Iterative Solver
Hybrid preconditioners are used for the iterative solver, as shown below. A multigrid preconditioner is a fast and memory-efficient iterative method and is used for acoustic pressure and magnetic vector potential. Two direct preconditioners are used by default: one for the coil current and the other for the solid displacement field. A direct preconditioner uses a direct solver as a preconditioner, which makes it possible to solve the dependent variables it includes using a direct solver. The hybrid approach allows for using a direct solver for the smaller fields in a multiphysics model that require less degrees of freedom and combines it with a multigrid iterative solver for other larger physics problems. This suggestion ensures that the coupled acoustic, structure, and electromagnetic problem is solved efficiently.
 A close-up of the Model Builder with Multigrid selected and the Settings window with Multi preconditioner selected.
A close-up of the Model Builder with Multigrid selected and the Settings window with Multi preconditioner selected.
 A close-up of the Model Builder with Direct Preconditioner 1 selected and the Settings window with Multi preconditioner selected.
A close-up of the Model Builder with Direct Preconditioner 1 selected and the Settings window with Multi preconditioner selected.
 A close-up of the Model Builder with Direct Preconditioner 2 selected and the Settings window with Multi preconditioner selected.
A close-up of the Model Builder with Direct Preconditioner 2 selected and the Settings window with Multi preconditioner selected.
To efficiently solve the coupled multiphysics problem, three hybrid preconditioners are used for the Suggested Iterative Solver (GMRES with GMG) : Multigrid (top), Direct Preconditioner 1 (middle), and Direct Preconditioner 2 (bottom).
Additional Solver and Convergence Considerations
When solving Maxwell’s equations formulated in terms of scalar and vector potentials, the potentials are not uniquely determined unless reference levels are specified. Therefore, in some scenarios, gauge fixing is recommended in order to improve numerical stability when solving the magnetic fields, as explained in the blog posts What Is Gauge Fixing? A Theoretical Introduction and How Do I Use Gauge Fixing in COMSOL Multiphysics®?. In the Magnetic Fields interface, there is a domain feature called Gauge Fixing for A-Field that can be used to ensure a unique and numerically stable solution to the equation solving for the magnetic vector potential . It enforces the gauge
and by adding an additional potential variable,
, and its associated conservation equation to the system. When the iterative solver has a hard time converging, you can apply this feature to all domains solved in the Magnetic Fields interface, as seen below.
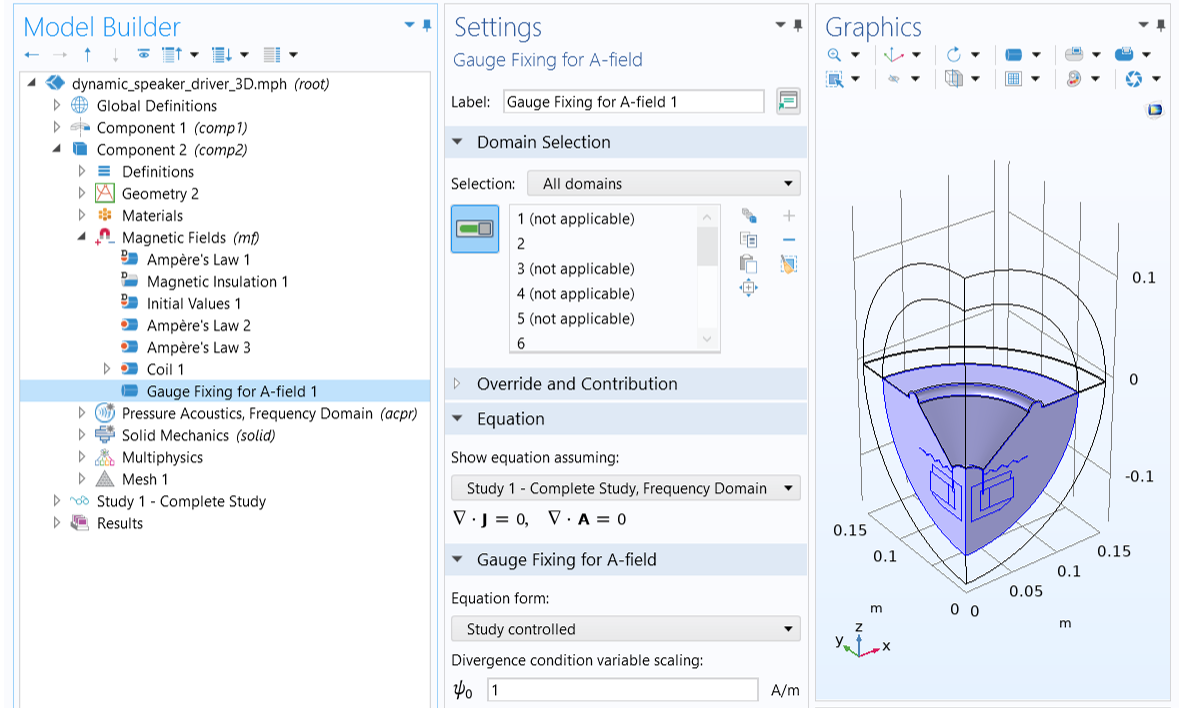 Applying Gauge Fixing for A-Field to the magnetic model to improve the iterative solver convergence.
Applying Gauge Fixing for A-Field to the magnetic model to improve the iterative solver convergence.
There is also a suggested iterative solver for models using Gauge Fixing for A-Field. If you add the gauge fixing later on, remember to reset the solver to the default setting in order to get the autogenerated iterative solver sequence.
In general, gauge fixing yields a more robust problem that requires less linear iterations. However, it is recommended not to use gauge fixing unless necessary since it increases the total number of unknowns, requiring more memory and a longer solving time for the iterations. The model example we use here does not use a gauge fixing because it can be solved without one and solves faster, even though it requires more linear iterations.
Submit feedback about this page or contact support here.