An einem hellen Abend im Jahr 1669 blickte Professor Erasmus Bartholinus durch ein Stück eines isländischen Kalzitkristalls, das er auf eine Bank gelegt hatte. Er beobachtete, dass ein Text auf der Bank, den er mit dem Stein bedeckte, als Doppelbild erschien. Bei dem beobachteten optischen Phänomen, das als Doppelbrechung bezeichnet wird, teilt sich ein Lichtstrahl beim Austritt aus einem Kristall in zwei parallele Strahlen auf. Hier zeigen wir einen Modellierungsansatz für diesen Effekt.
Anisotrope Materialien Verstehen
Der Lichtstrahl, den Erasmus Bartholinus beim geraden Durchqueren des Kristalls beobachtet hat, wird als ordentlicher Strahl bezeichnet. Der andere Lichtstrahl, der sich beim Durchqueren des Kristalls biegt, ist ein außerordentlicher Strahl. Anisotrope Materialien, wie der Kristall aus dem oben beschriebenen Stein-und-Bank-Experiment, finden sich in Anwendungen, die von der Erkennung schädlicher Gase bis zur Strahlenteilung für photonische integrierte Schaltungen reichen.
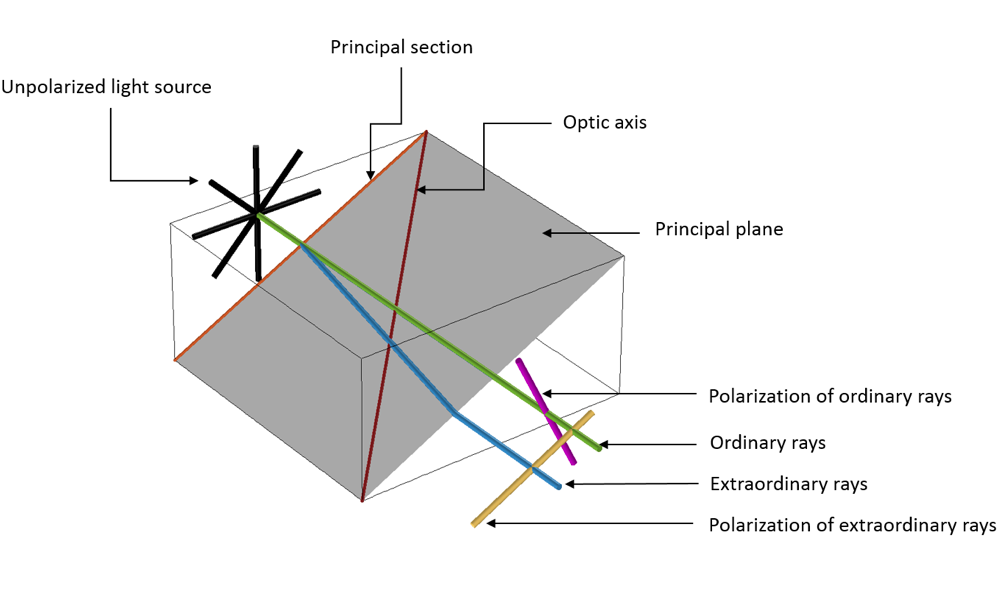
Ordentliche und außerordentliche Strahlen auf dem Weg durch einen anisotropen Kristall.
Physikalisch ausgedrückt polarisiert ein unpolarisierter elektromagnetischer Lichtstrahl, der sich durch ein anisotropes dielektrisches Material ausbreitet, den dielektrischen Bereich, was zu einer Verteilung von Ladungen führt, die als elektrische Dipole bekannt sind. Dieses Phänomen führt zu induzierten Feldern innerhalb des anisotropen dielektrischen Materials, in dem zwei Arten von Wellen zwei unterschiedliche Brechungsindizes (ordentlich und außerordentlich) erfahren.
Die ordentliche Welle ist senkrecht zur Hauptebene und die außerordentliche Welle parallel zur Hauptebene polarisiert, wobei die Hauptebene von der optischen Achse und den beiden Ausbreitungsrichtungen im Kristall aufgespannt wird. Aufgrund dieses Verhaltens breiten sich die Wellen mit unterschiedlichen Geschwindigkeiten und Trajektorien aus.
Einführung der Anisotropie in Silizium-Wellenleitern
In einem vorherigen Blog-Beitrag haben wir über Silizium gesprochen und darüber, wie sein Derivat, Siliziumdioxid, aufgrund seiner Kompatibilität mit der CMOS-Fertigungstechnik in großem Umfang in photonischen integrierten Chips verwendet wird. Massives Silizium, das eine isotrope Eigenschaft hat, wird zur Entwicklung von Prototypen für photonische integrierte Chips verwendet. Aufgrund einzigartiger optischer Eigenschaften wie der Aufspaltung von Strahlen und polarisationsbasierter optischer Effekte kommt die Anisotropie dann später ins Spiel.
Anisotropie in der Silizium-Photonik entsteht unbeabsichtigt durch den Ausglühprozess bei der Fertigung des Wellenleiters. Der Unterschied in der thermischen Ausdehnung zwischen Kern und Mantel führt zu einer Geometrieabweichung aufgrund von spannungsoptischen Effekten, die zu Effekten wie Modenaufspaltung und Impulserweiterung führen. Anisotropie kann auch absichtlich eingeführt werden, indem die Porosität von Siliziumdioxid variiert wird. Auf diese Weise können die Forscher mit einer Reihe von effektiven Brechungsindizes arbeiten, die von Siliziumdioxid (n ~ 1,44) bis zu Luft (n ~ 1) reichen, was ihnen den Vorteil verschafft, sehr empfindliche optische Sensoranwendungen durchführen zu können.
Optische Ausbreitungsmodi
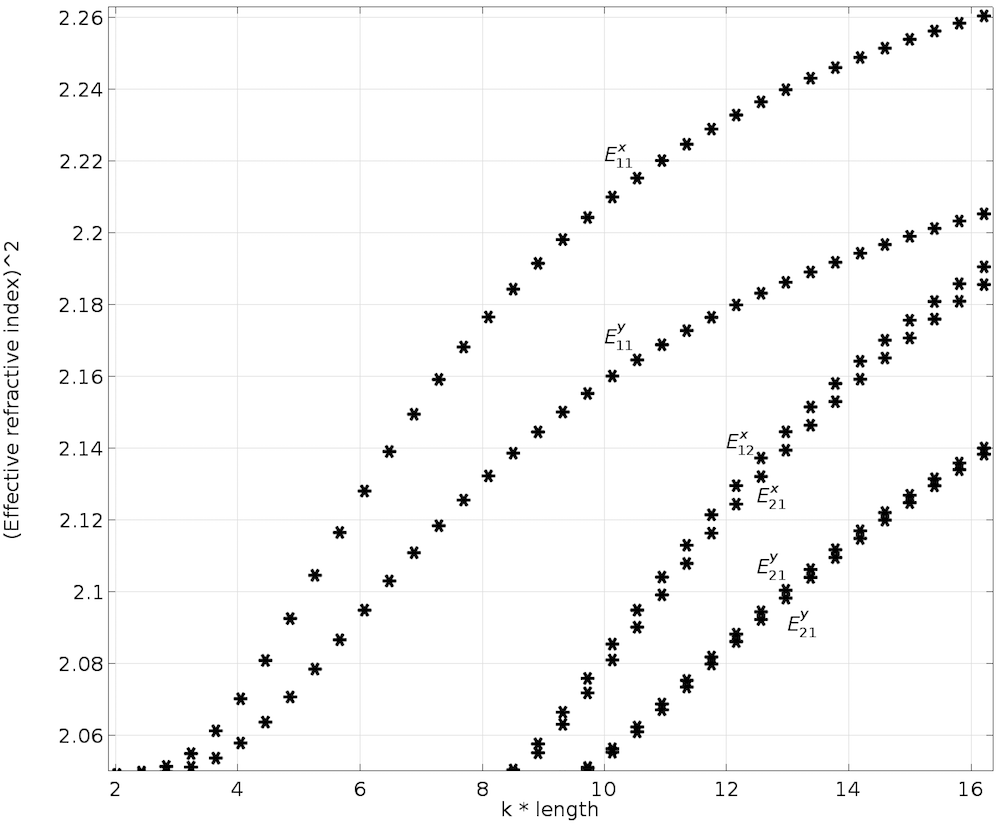
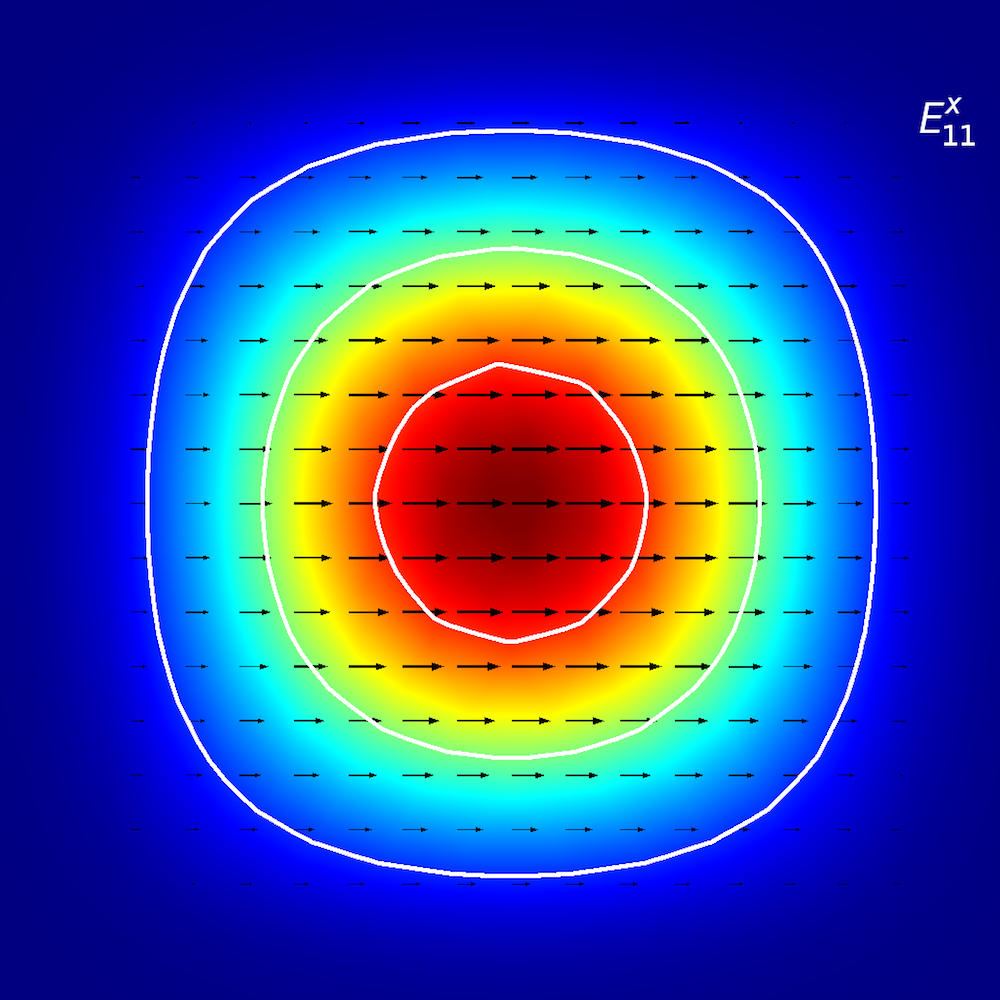
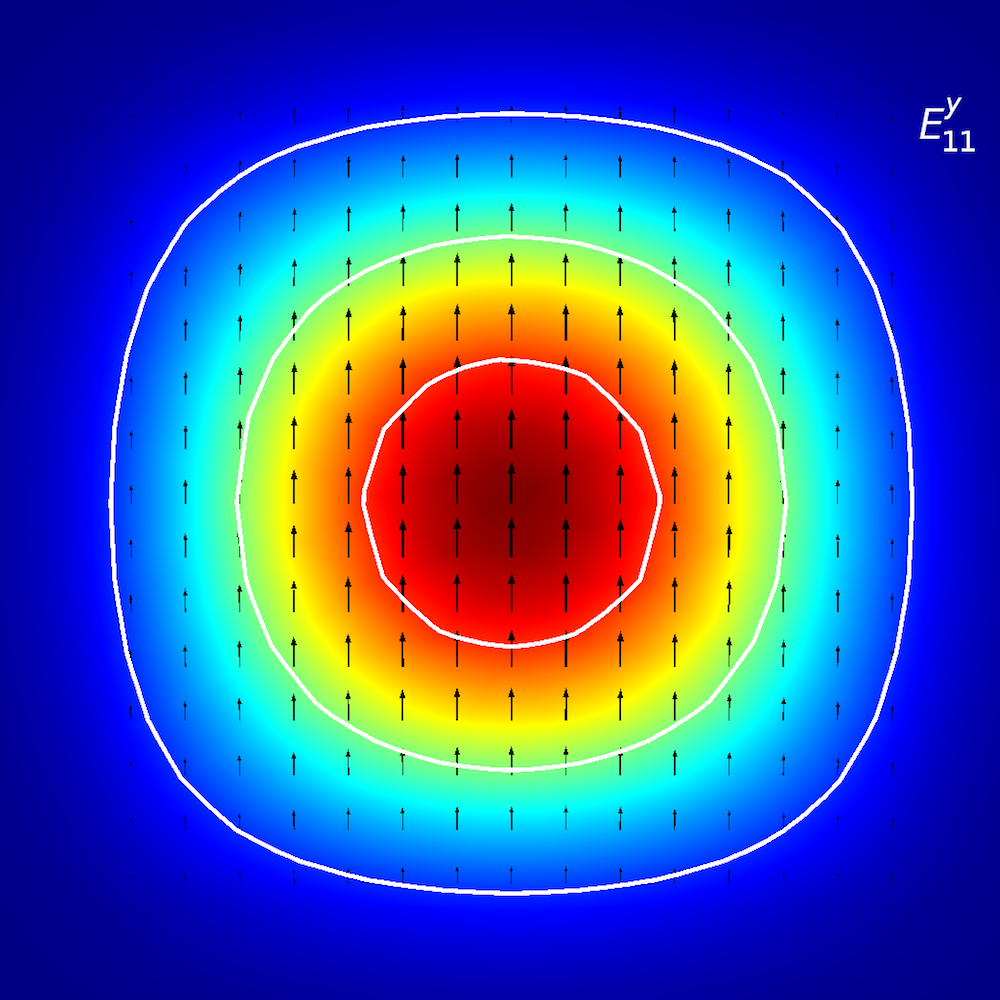
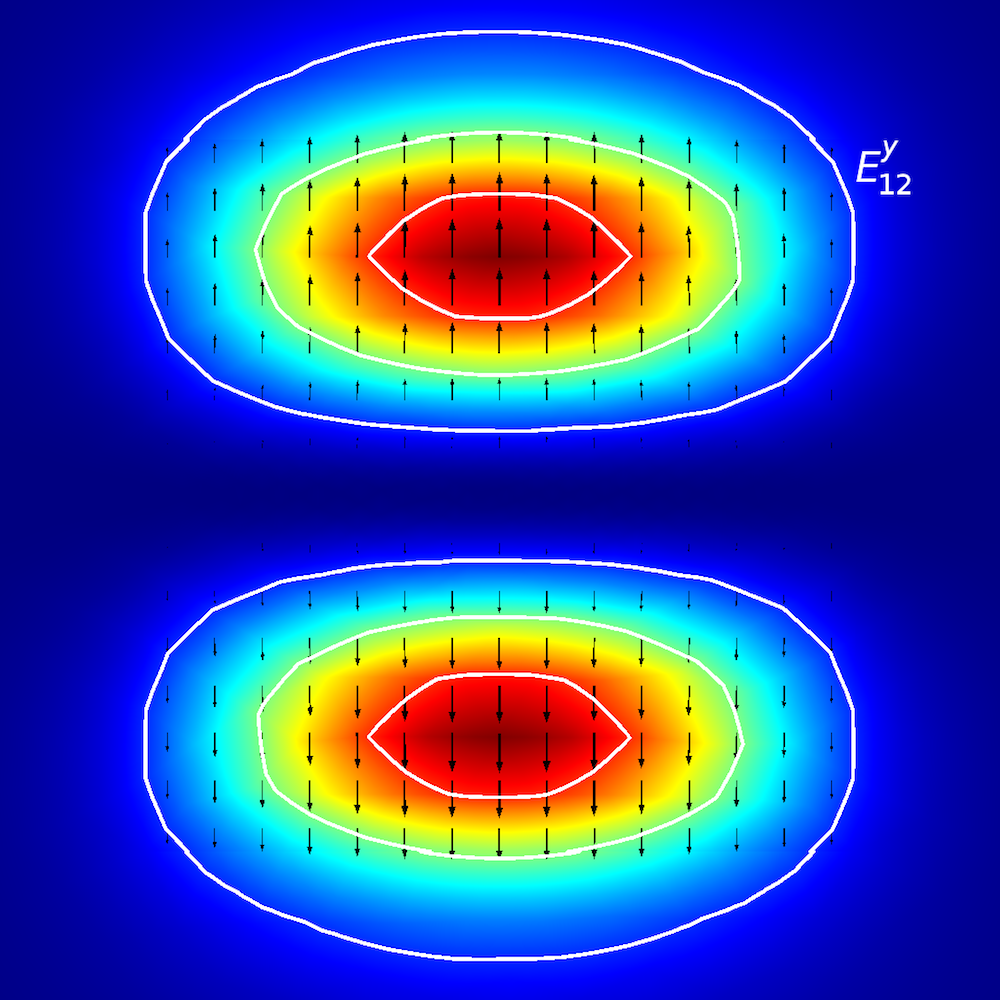
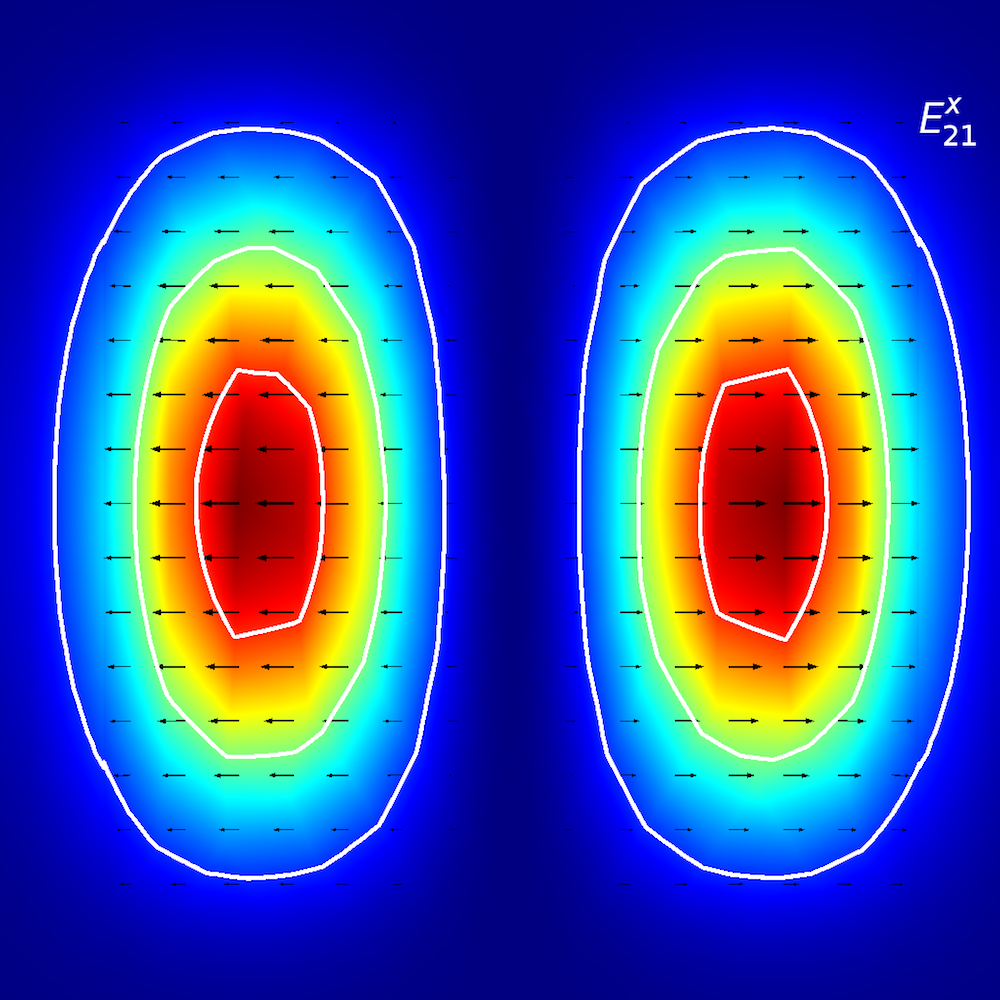
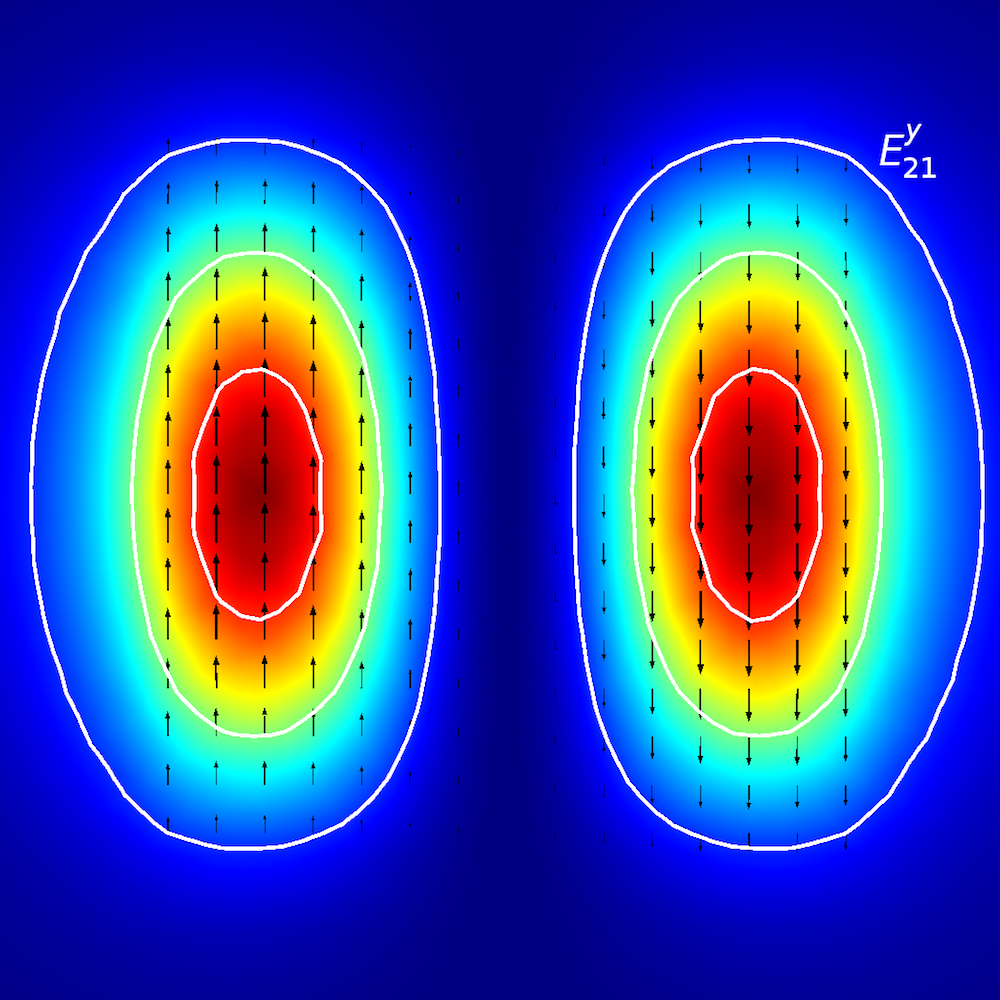
Zur qualitativen Analyse anisotroper Medien untersuchen die Forscher, wie sich optische Energie in planaren Wellenleitern ausbreitet (auch als Ausbreitungsmoden bezeichnet). In planaren Wellenleitern definieren wir Moden durch E^{x}_{p,q}– und E^{y}_{p,q}-Terminologie (Ref. 2), wobei x und y die Richtung der Polarisation und p und q die Anzahl der Maxima in den x– und y-Koordinaten anzeigen.
Stellen Sie sich das so vor: Sie laufen auf einer E^{x}_{2,1}-“Landschaft” (wie unten dargestellt). Die “Winde” (Polarisation) verlaufen entlang der ±x-Richtung, und Sie treffen auf zwei verschiedene Spitzen, wenn Sie sich von der –x– in die +x-Richtung bewegen. Wenn Sie sich von der –y– in die +y-Richtung bewegen, beobachten Sie beide Spitzen gleichzeitig.
Modenanalyse des planaren Wellenleiters. Obere Reihe, von links nach rechts: E^{x}_{1,1} und E^{y}_{1,1}. Mittlere Reihe, von links nach rechts: E^{x}_{1,2} und E^{y}_{1,2}. Untere Reihe, von links nach rechts: E^{x}_{2,1} und E^{y}_{2,1}. Der Pfeilplot stellt das elektrische Feld dar; Kontur- und Oberflächenplot stellen den Leistungsfluss außerhalb der Ebene dar (rot ist eine hohe und blau eine geringe Magnitude).
Analyse anisotroper Strukturen in der COMSOL Multiphysics® Software
Bevor man einen Lichtstrahl mit einer Laserquelle durch einen Wellenleiter schickt, muss man wissen, welche optischen Moden innerhalb einer bestimmten Kern-/Manteldimension des Wellenleiters bestehen bleiben können. Die Durchführung einer Modenanalyse mit einem vollvektoriellen Finite-Elemente-Tool wie der COMSOL Multiphysics® Software kann sehr hilfreich sein, um die optischen Moden bzw. die Dispersionskurve qualitativ und quantitativ zu analysieren.
Einführung der diagonalen Anisotropie
Die Durchführung einer Modalanalyse für ein isotropes Material erfordert die Definition eines einzigen komplexen Wertes, während im Falle eines anisotropen Materials ein Ansatz erforderlich ist, bei dem die relative Permittivität als Tensor definiert wird. Die elektrische Permittivität setzt im Wesentlichen das elektrische Feld mit der Materialeigenschaft in Beziehung. Hier bezieht sich Tensorauf eine 3×3-Matrix, die sowohl diagonale (\epsilonxx, \epsilonyy, \epsilonzz) als auch außerdiagonale (\epsilonxy, \epsilonxz, \epsilonyx, \epsilonyz, \epsilonzx, \epsilonzy) Terme hat, wie unten dargestellt.
\epsilon_{xx}&\epsilon _{xy}&\epsilon _{xz}\\
\epsilon _{yx}&\epsilon _{yy}&\epsilon _{yz}\\
\epsilon _{zx}&\epsilon _{zy}&\epsilon _{zz}\\
\end{bmatrix}
Für alle Materialien lässt sich jedoch ein Koordinatensystem finden, in dem nur die Diagonalelemente des Permittivitätstensors ungleich Null sind, während die Außendiagonalelemente alle Null sind. Die drei Koordinatenachsen in diesem gedrehten Koordinatensystem sind die Hauptachsen des Materials, und dementsprechend werden die drei Werte für die Diagonalelemente im Permittivitätstensor als die Hauptpermittivitäten des Materials bezeichnet.
Es gibt grundsätzlich zwei Arten von anisotropen Kristallen: uniaxiale und biaxiale Kristalle. Bei geeigneter Wahl des Koordinatensystems, in dem nur die Diagonalelemente des Permittivitätstensors ungleich Null sind, gilt für die optischen Eigenschaften, dass uniaxialer Kristall nur die diagonalen Terme berücksichtigt, also \epsilonxx = \epsilonyy = (no)2, \epsilonzz = (ne)2, wobei no und ne die ordentlichen und außerordentlichen Brechungsindizes sind. Wenn jedoch \epsilon_{xx}\neq \epsilon_{yy} \neq \epsilon_{zz}, ist dies als biaxialer Kristall bekannt.
Um dieses Argument in eine Modellierungsperspektive zu bringen, können wir das Beispiel des Buried Rib Waveguides aus diesem Blogbeitrag über Silizium-Photonik-Design erweitern. Wir können eine Modalanalyse für den 2D-Querschnitt des Wellenleiters mit einer quadratischen Kern- und Mantellänge von 4 µm bzw. 20 µm durchführen (siehe unten). Die Betriebswellenlänge wird in allen Fällen mit 1,55[µm] angenommen.

Schematische Darstellung eines optischen 3D Buried Rib Waveguides, bei dem die Modenanalyse am 2D-Querschnitt des Einlasses durchgeführt wurde. Das Intensitätsdiagramm und das Pfeildiagramm stellen die Moden bzw. die Polarisation der E-Felder dar.
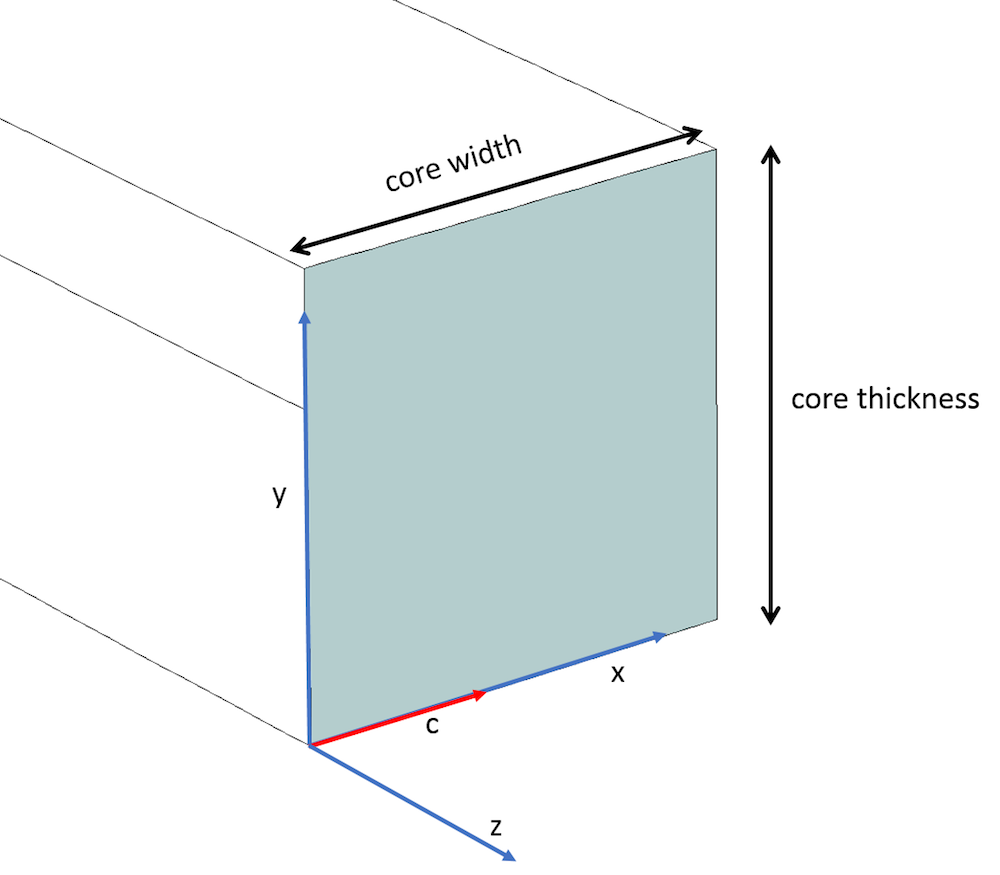
Kern des Rib Waveguides mit Darstellung der optischen Achse (rot) entlang der x-Achse und der Hauptachse (blau).
Im klassischen Fall eines einachsigen Materials nehmen wir an, dass die optische Achse (d.h., c-Achse) entlang der Hauptachse x verläuft (wie oben gezeigt) und betrachten die \epsilonyy– und \epsilonzz-Terme der diagonalen relativen Permittivität (die orthogonal zur c-Achse stehen) als das Quadrat des ordentlichen Brechungsindexes (~1,51992 ~ 2,31). Das \epsilonxx-Komponentenelement entlang der c-Achse wird als das Quadrat des außerordentlichen Brechungsindexes betrachtet (~1,47992 ~ 2,19) (wie in Ref. 3). Außerdem werden die außerdiagonalen Terme als Null betrachtet (wie unten gezeigt), und die Ummantelung hat eine isotrope relative Permittivität (~1,43182). Die abgeleiteten optischen Moden sind die 6 oben dargestellten Moden. Beachten Sie den Unterschied in den Brechungsindizes: “nxx – nyy” ist als Doppelbrechung bekannt, bei der nxx = \sqrt{\epsilon_{xx}} und nyy = \sqrt{\epsilon_{yy}} sind.
\begin{bmatrix}
2,19 & 0 & 0 \\
0 & 2,31 & 0\\
0 & 0 & 2,31\\
\end{bmatrix}
Relativer Permittivitätstensor mit Diagonalelementen.
Dispersionskurven
Durch die Auswertung der optischen Moden können wir das Verhalten des Lichtwellenleiters visuell nachvollziehen. Die Dispersionskurven können jedoch auch für die Durchführung quantitativer Analysen nützlich sein. Eine Dispersionskurve stellt die Veränderung des effektiven Brechungsindexes in Abhängigkeit von der Länge des Wellenleiters oder der Betriebsfrequenz dar.
Diagonale Anisotropie
Es wird eine Modalanalyse durchgeführt, während die Länge des Wellenleiters parametrisch von 0,5 µm bis 4 µm verschoben wird, um die Dispersionskurve für den anisotropen Kern abzuleiten, wie in der Abbildung unten dargestellt. Wir gehen von dem oben genannten Fall aus, mit diagonalen Anisotropietermen des Kerns (i.e., \epsilonxx = 2,19, \epsilonyy = \epsilonzz = 2,31 und alle Außerdiagonalelemente sind Null). Die Ergebnisse werden mit denen von Koshiba et al. verglichen. (Ref. 3).
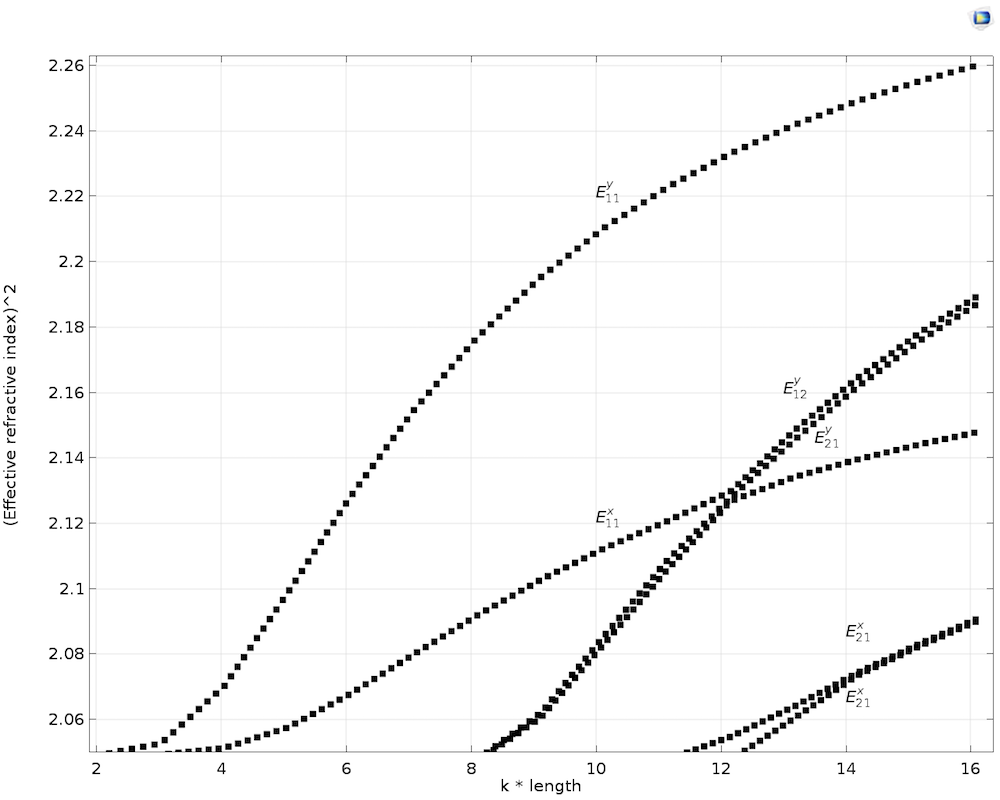
Dispersionskurve mit transversalem anisotropem Kern.
Außerdiagonale Transversale Anisotropie (XY-Ebene)
Wenn die optische Achse (d. h. die c-Achse) in der XY-Ebene liegt und einen Winkel von \theta mit der x-Achse bildet, sind die diagonalen Komponenten \epsilonxx, \epsilonyy, \epsilonzz und die außerdiagonalen Komponenten \epsilonxy und \epsilonyz ungleich Null, während die übrigen Komponenten gleich Null sind. Der vollständige relative Permittivitätstensor kann mit Hilfe der Rotationsmatrix [R] wie unten gezeigt ausgewertet werden, wobei die Rotationsmatrix [R] speziell für die Drehung der c-Achse in der XY-Ebene bestimmt ist. \epsilonxx ist das Quadrat des außerordentlichen Brechungsindex (~2,19), weil die c-Achse entlang der Hauptachse x liegt, während \epsilonyy und \epsilonzz das Quadrat des ordentlichen Brechungsindex (~2,31) sind. Die außerdiagonalen Elemente \epsilonxy und \epsilonyz ergeben sich aus der Multiplikation der Matrizen wie unten angegeben.
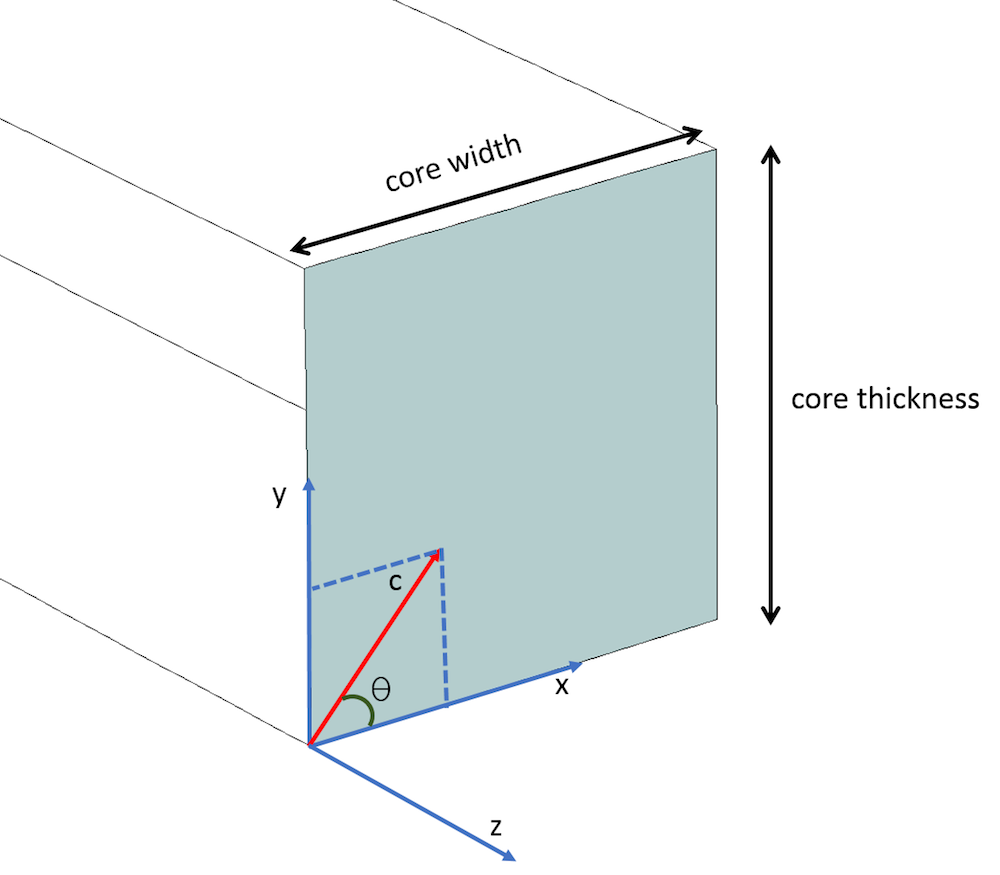
Die c-Achse liegt in der XY-Ebene und bildet einen Winkel von \theta mit der x-Achse.
\begin{bmatrix}
cos(\theta) & -sin(\theta) & 0 \\
sin(\theta) & cos(\theta) & 0\\
0 & 0 & 1\\
\end{bmatrix}
\begin{bmatrix}
\epsilon_{xx} & 0 & 0 \\
0 & \epsilon_{yy} & 0 \\
0 & 0 & \epsilon_{zz} \\
\end{bmatrix}
\begin{bmatrix}
cos(\theta) & sin(\theta) & 0 \\
-sin(\theta) & cos(\theta) & 0\\
0 & 0 & 1\\
\end{bmatrix}
\begin{bmatrix}
(\epsilon_{xx}) cos^2(\theta) + (\epsilon_{yy}) sin^2(\theta) & (\epsilon_{xx}) sin(\theta) cos(\theta)-(\epsilon_{yy}) sin(\theta) cos(\theta) & 0 \\
(\epsilon_{xx}) sin(\theta)cos(\theta)-(\epsilon_{yy})sin(\theta)cos(\theta) & (\epsilon_{yy}) cos^2(\theta) + (\epsilon_{xx}) sin^2(\theta) & 0\\
0 & 0 & \epsilon_{zz}\\
\end{bmatrix}
Der relative Permittivitätstensor ε wird zusammen mit einer Rotationsmatrix behandelt, die c-Achse wird in der XY-Ebene mit dem Winkel \theta gedreht.
Schließlich folgt die Modalanalyse des Wellenleiters mit anisotropem Kern und isotropem Mantel, bei dem die optische Achse einen Winkel von 0, 15, 30 und 45 Grad mit der Hauptachse x bildet, wie unten dargestellt. Hier kann beobachtet werden, dass sich die Richtung des Magnetfeldes in der Ebene mit der Änderung des Winkels der optischen Achse ändert. Die Dispersionskurve kann auch abgebildet werden, indem die Länge des Kerns und der Ummantelung parametrisch von 0,5 µm bis 4 µm verschoben wird, wobei der Winkel \theta mit 45° angenommen wird. Die Dispersionskurve ähnelt tendenziell der Dispersionskurve der diagonalen Anisotropie, wie oben beschrieben.
Modenanalyse, einschließlich außerdiagonaler Terme, für θ = 0° (oben links), θ = 15° (oben rechts), θ = 30° (unten links) und θ = 45° (unten rechts). Die Abbildung zeigt die Magnetfeldlinien innerhalb des Kerns für verschiedene Drehwinkel.
Außerdiagonal-Längsanisotropie (YZ-Ebene)
Betrachtet man schließlich die Längsanisotropie, bei der die optische Achse (d. h. die c-Achse) in der YZ-Ebene liegt und einen Winkel von \phimit der y-Achse bildet, sind die diagonalen Komponenten \epsilonxx, \epsilonyy, \epsilonzz und die außerdiagonalen Komponenten \epsilonyz und \epsilonzy ungleich Null, während die übrigen Komponenten Null sind. Der relative Permittivitätstensor kann mit Hilfe der Rotationsmatrix [R] wie unten gezeigt ausgewertet werden, wobei die Rotationsmatrix [R] speziell für die Rotation der c-Achse in der YZ-Ebene bestimmt ist. \epsilonyy ist das Quadrat des außerordentlichen Brechungsindex (~2,19), weil die c-Achse entlang der Hauptachse liegt y, während \epsilonxx, \epsilonzzist das Quadrat des ordentlichen Brechungsindex (~2,31). Die außerdiagonalen Elemente \epsilonyz und \epsilonzy ergeben sich aus der Multiplikation der Matrizen wie unten angegeben.
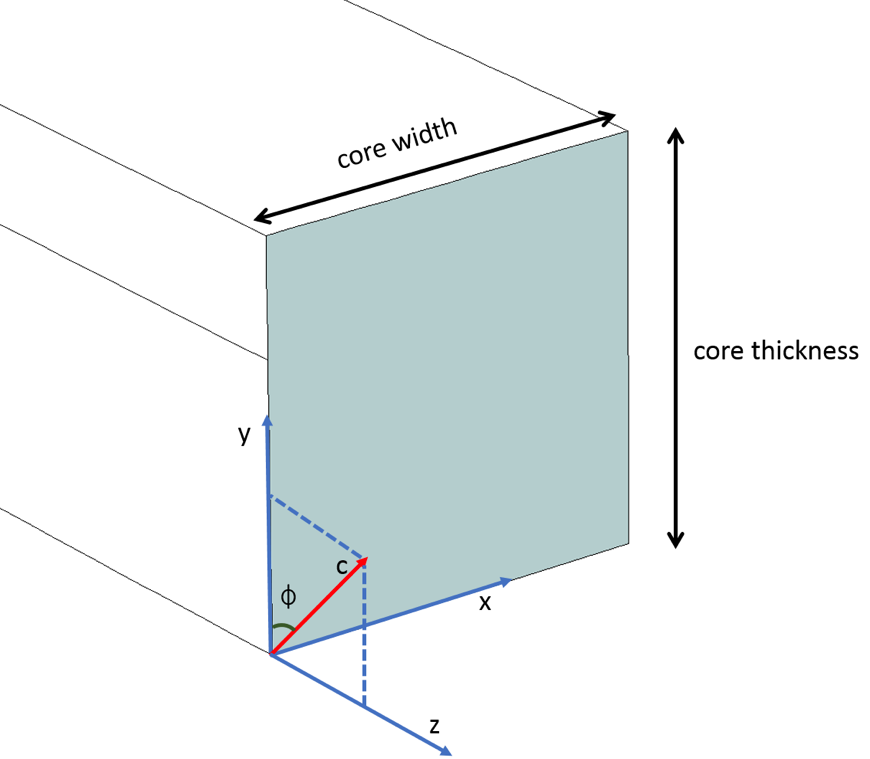
Die c-Achse liegt in der YZ-Ebene und bildet einen Winkel von \phi mit der x-Achse.
\begin{bmatrix}
1 & 0 & 0 \\
0 & cos(\phi) & -sin(\phi)\\
0 & sin(\phi) & cos(\phi) \\
\end{bmatrix}
\begin{bmatrix}
\epsilon_{xx} & 0 & 0 \\
0 & \epsilon_{yy} & 0 \\
0 & 0 & \epsilon_{zz} \\
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & cos(\phi) & sin(\phi)\\
0 & -sin(\phi) & cos(\phi) \\
\end{bmatrix}
\begin{bmatrix}
\epsilon_{xx} & 0 & 0 \\
0 & (\epsilon_{yy}) cos^2(\phi) + (\epsilon_{zz}) sin^2(\phi) & (\epsilon_{yy})sin(\phi)cos(\phi)-(\epsilon_{zz}) sin(\phi)cos(\phi)\\
0 & (\epsilon_{yy})sin(\phi)cos(\phi)-(\epsilon_{zz}) sin(\phi)cos(\phi) & (\epsilon_{zz}) cos^2(\phi) + (\epsilon_{yy}) sin^2(\phi)\\
\end{bmatrix}
Der relative Permittivitätstensor ε wird zusammen mit einer Rotationsmatrix behandelt, die in der YZ-Ebene um den Winkel \phi rotiert.
Anschließend wird eine Modalanalyse durchgeführt, bei der die Länge des Wellenleiters parametrisch von 0,5 um bis 4 um verschoben wird, um die Dispersionskurve für den längsgerichteten anisotropen Kern abzuleiten, wie in der Abbildung unten dargestellt. In diesem Fall gilt \phi = 45° (d.h. die c-Achse liegt in der YZ-Ebene und bildet 45° mit der y-Achse) (Ref. 3).
Ausbreitungskurve mit längsanisotropem Kern.
Abschließende Überlegungen zur Modellierung anisotroper Materialien
In diesem Blogbeitrag haben wir qualitative Analysen (Ausbreitungsmoden) und quantitative Analysen (Dispersionskurven) des anisotropen Lichtwellenleiters mithilfe der Modenanalyse in COMSOL Multiphysics® durchgeführt. Diagonale Anisotropie sowie außerdiagonale transversale und längsgerichtete Anisotropie wurden betrachtet, um ihre Dispersionsbeziehungen herzuleiten. Diese Art von Analysen gibt uns mehr Flexibilität bei der Optimierung von Material- und Geometrieparametern und hilft uns, ein tiefes und intuitives Verständnis der Physik anisotroper Materialien zu erlangen.
Ein einfaches Übungsmodell für den Einstieg ist die Step-Index-Faser, bei der die Modenanalyse über einen 2D-Querschnitt der 3D-Lichtleitfaser erfolgt.
Nächste Schritte
Um diese Modelle auszuprobieren, klicken Sie auf die Schaltfläche unten.
h3>Aktuelle Liste der Blogbeiträge in der Silizium-Photonik-Serie
Referenzen
- E. Hecht, Optics, Pearson.
- E.A.J. Marcatili, “Dielectric rectangular waveguide and directional coupler for integrated optics”, Bell Syst. Tech. J., vol. 48, pp. 2071–2102, 1969.
- M. Koshiba, K. Hayata, and M. Suzuki, “Finite-element solution of anisotropic waveguides with arbitrary tensor permittivity,” Journal of Lightwave Technology, vol. 4, no. 2, pp. 121–126, 1986.











Kommentare (0)