Schätzen von Pi mit der Monte-Carlo-Methode und Particle Tracing

Wenn es eine Zahl gibt, die die gesamte Mathematik und Wissenschaft beherrscht, dann ist es wohl Pi. Dieses kleine Symbol, π, hat eine lange Geschichte, die Tausende von Jahren zurückreicht. Von alten Zivilisationen, die grobe Annäherungen über Kreise machten, bis hin zu modernen Supercomputern, die Billionen von Ziffern berechnen, hat Pi die Phantasie von Mathematikern und Neugierigen gleichermaßen beflügelt. In diesem Blog-Beitrag stellen wir Ihnen einen unterhaltsamen und beliebten Ansatz zur Berechnung von Pi vor, der die Features der Simulationssoftware COMSOL Multiphysics^® nutzt.

Näherungen von Pi im Lauf der Geschichte

Die frühesten bekannten Näherungen von Pi finden sich in antiken Zivilisationen. Mathematiker aus Babylon hatten Pi auf 3 angenähert, was für die Durchführung architektonischer Projekte zu jener Zeit angemessen war, bevor sie die Zahl auf einen Wert von 3,125¹ verfeinerten. Mathematiker in Ägypten und Gelehrte in Indien lieferten ähnliche Werte, indem sie die Fläche eines Kreises und eines Achtecks² bzw. astronomische Berechnungen³ verglichen. Ein bedeutender Durchbruch gelang griechischen Gelehrten, darunter Archimedes, der geometrische Methoden einsetzte, um Pi bis auf 3 Größenordnungen genau zu bestimmen⁴.

Links: Archimedes, 1620 (auch bekannt als Bildnis eines Gelehrten) von Domenico Fetti. Bild gemeinfrei über Wikimedia Commons. Rechts: Ein Porträt von Leonardo Fibonacci. Bild gemeinfrei über Wikimedia Commons.

Der populäre Näherungswert von 3,14, den wir heute alle verwenden, stammt von dem chinesischen Mathematiker Liu Hui, der ihn für praktische Zwecke vorschlug⁵. Spätere Entwicklungen bei der Berechnung von Pi beinhalteten die Auswertung von unendlichen Reihen und die Nutzung trigonometrischer Beziehungen. Mithilfe der Infinitesimalrechnung waren Mathematiker in der Lage, unendliche Reihen abzuleiten, die zur Berechnung von Pi mit einem hohen Maß an Genauigkeit verwendet werden konnten. Die wichtigsten Beiträge dazu lieferten Fibonacci und Al-Khwarizmi.

Diese Entwicklungen legten den Grundstein für die modernen Methoden, einschließlich derer, die in Computeralgorithmen verwendet werden, um Pi mit einer extrem hohen Genauigkeit zu berechnen, indem fortschrittliche Mathematik und Rechenleistung zur Berechnung von Billionen von Ziffern eingesetzt werden. Zu den bemerkenswerten Berechnungsmethoden gehören der Chudnovsky-Algorithmus, der Gauß-Legendre-Algorithmus, die Machin-Formel und vor allem die Monte-Carlo-Methode.

Die Monte-Carlo-Methode, einfach erklärt

Die Monte-Carlo-Methode ist eine Rechentechnik, die sich auf Zufallsstichproben stützt, um numerische Ergebnisse zu schätzen. Sie ist besonders nützlich für Probleme mit einer großen Anzahl von Variablen, bei denen eine inhärente Zufälligkeit genutzt werden kann, um ein deterministisches Problem zu lösen. Stellen Sie sich vor, Sie versuchen zu berechnen, wie viel Pizza Sie für eine Party bestellen sollen. Das deterministische Problem besteht darin, herauszufinden, wie viele Stücke jede Person essen wird. Anstatt jede Person zu fragen, wie viele Stücke sie essen würde, und das Ergebnis zu addieren (was bei einer großen Party ziemlich umständlich sein kann), könnten Sie einige Freunde zufällig auswählen, sie fragen, wie viele Stücke sie essen würden, und dann den Durchschnitt bilden, um das Problem zu lösen. Das ist ein bisschen wie die Monte-Carlo-Methode – die Verwendung von Zufallsstichproben, um einen Wert zu schätzen. Monte-Carlo-Methoden werden häufig für Simulationen komplexer Phänomene, wie Strömungen, statistische Mechanik, Biochemie, Kryptographie, Soziologie und Psychologie, verwendet.

Diese Ideologie lässt sich auf eine beliebte und unterhaltsame Methode zur Schätzung von Pi ausweiten. Dabei werden nach dem Zufallsprinzip Punkte in einem Quadrat platziert und gezählt, wie viele davon innerhalb eines Kreises im Quadrat liegen. Das Verhältnis der Punkte innerhalb des Kreises zur Gesamtzahl der Punkte kann verwendet werden, um Pi zu schätzen. Da die Fläche eines Kreises in einem Quadrat mit der Seite 2r πr² und die Fläche eines Quadrats (2r)² = 4r² beträgt, ist das Verhältnis ihrer Flächen π/4. Das bedeutet, dass die Wahrscheinlichkeit, dass ein Punkt im Inneren des Kreises landet, π/4 ist. Wenn wir also das Verhältnis der Punkte innerhalb des Kreises zur Gesamtzahl der Punkte mit 4 multiplizieren, erhalten wir eine Schätzung von π. Je mehr Punkte wir verwenden, desto genauer wird unsere Schätzung. Denn mit zunehmender Anzahl von Punkten konvergiert das Verhältnis gegen den tatsächlichen Wert von π/4.

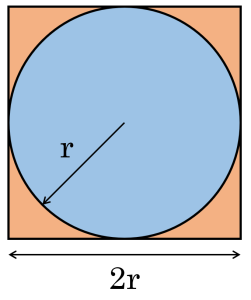
Die Grundlage für die Schätzung von Pi.

Schätzen von Pi mit der Monte-Carlo-Methode in COMSOL Multiphysics^®

Für diese einfache Monte-Carlo-Simulation nutzen wir das Interface Mathematical Particle Tracing, das verfügbar ist, wenn Sie das Particle Tracing Module zur Softwareplattform COMSOL Multiphysics^® hinzufügen. Obwohl Nutzer dieses Moduls es in der Regel nicht verwenden, um einfach nur zufällig Punkte zu generieren, haben wir uns entschieden, es in unserem Beispiel zu Visualisierungs- und Ästhetikzwecken zu nutzen.

Nun zu dem Beispiel. Die Partikel werden nach dem Zufallsprinzip auf einem quadratischen Gebiet freigesetzt und bleiben dort stationär. Die Anzahl der Partikel, die sich innerhalb des kreisförmigen Bereichs befinden, wird verfolgt, um eine Echtzeit-Schätzung von Pi zu erhalten. Wir sehen, dass sich der geschätzte Wert (durchgezogene blaue Linie) mit zunehmender Anzahl von Punkten dem wahren Wert (gestrichelte grüne Linie) annähert. Es ist wichtig zu beachten, dass die Genauigkeit des geschätzten Wertes nicht linear mit der Anzahl der Punkte variiert. Der statistische Fehler bei der Monte-Carlo-Approximation ist in der Regel proportional zu 1/sqrt(n). Das bedeutet, dass Sie die Anzahl der Punkte in der Regel um den Faktor 100 erhöhen müssen, um den Fehler um einen Faktor 10 zu verringern.

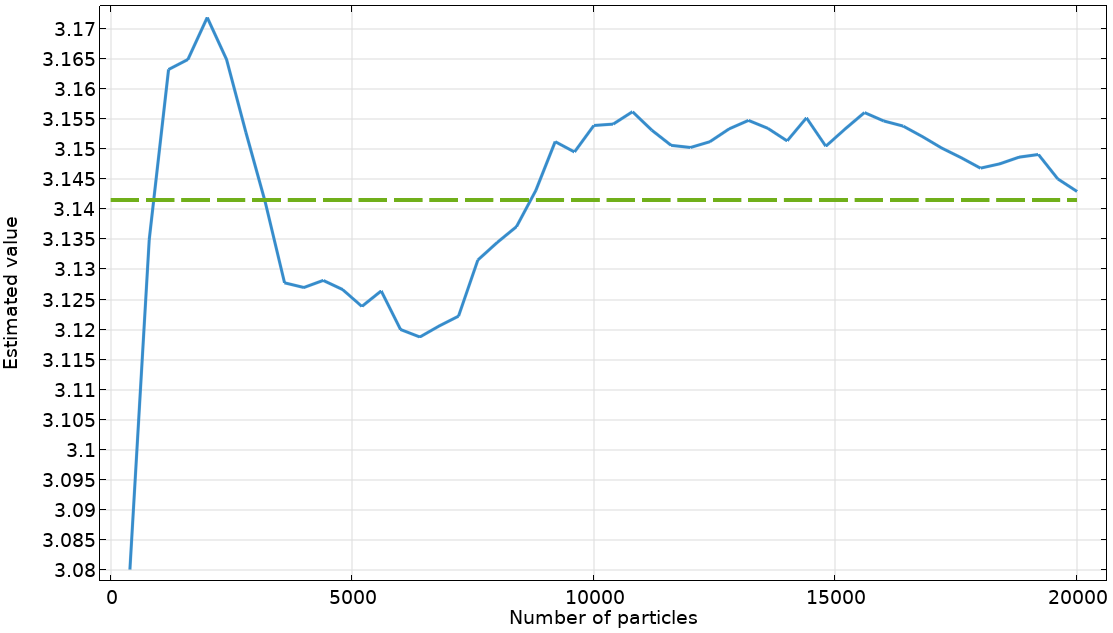
Ein Vergleich zwischen der Echtzeit-Schätzung von Pi (durchgezogene blaue Linie) und seinem wahren Wert (gestrichelte grüne Linie) für eine zunehmende Anzahl von zufällig platzierten Punkten.

Als nächstes haben wir den Application Builder in COMSOL Multiphysics^® verwendet, um eine App auf der Grundlage dieses Modells zu erstellen. Die App ermöglicht es uns, die Anzahl der Punkte mit einem Schieberegler zu variieren und wir erhalten in Echtzeit den geschätzten Wert von Pi und den Fehler gegenüber dem wahren Wert. Die App visualisiert auch die zufällig platzierten Punkte, die farblich gekennzeichnet sind, um die Punkte zu identifizieren, die innerhalb des Kreises liegen.

Eine Bildschirmaufnahme von jemandem, der die App verwendet, um Pi auf der Grundlage einer unterschiedlichen Anzahl von Punkten zu schätzen und eine visuelle Interpretation der Ergebnisse zu erhalten.

Nächste Schritte

Sie können die MPH-Datei mit der App und den zugehörigen Dateien aus der Application Gallery herunterladen: Using the Monte Carlo Method to Estimate the Value of Pi.

• Weitere Modelle, die die Monte-Carlo-Methode verwenden:
  • Ein Beispiel, das zeigt, wie man eine direkte Monte-Carlo-Simulation der Ishigami-Funktion durchführt
  • Ein Modell, das die Monte-Carlo-Methode verwendet, um die Leistung einer einfachen Turbomolekularpumpe mit freier Molekularströmung zu bewerten
  • Ein Modell, das die Transmissionswahrscheinlichkeit durch eine S-förmige Geometrie mittels der Monte-Carlo-Methode berechnet
• Informationen über den Application Builder:
  • Lesen Sie im Blog-Beitrag Multiphysics Simulation Is More Accessible with the Application Builder, was unsere Kunden über den Application Builder zu sagen haben.
  • Lesen Sie den Artikel Forecasting Fruit Freshness with Simulation-Apps über eine Smartphone-App, die auf Multiphysik-Simulationen basiert.
  • Erfahren Sie im Bericht Bringing Lab Courses to Remote Learning Students with Simulations-Apps, wie ein Universitätsprofessor Apps im Unterricht einsetzt.

Referenzen

1. P. Beckmann, A History of π. New York: St. Martin’s Press, 1971
2. C. Rossi, Architecture and Mathematics in Ancient Egypt. Cambridge University Press, 2004
3. C. Krishna, A profile of Indian culture. Indian Book Company, 1975
4. D.B. Damini & A. Dhar, How Archimedes showed that pi is approximately equal to 22/7. arXiv e-prints, 2020
5. Y. Lam & T.S. Ang, Circle measurements in ancient China, Historia Mathematica, 1986