
Many polymers and biological tissues exhibit viscoelastic deformation, which has a time-dependent response even if the loading is constant in time. Linear viscoelasticity, where the stress depends linearly on the strain and strain rate, is a common approximation. We usually assume that the viscous part of the deformation is incompressible, so the volumetric deformation is purely elastic. As of COMSOL Multiphysics® 5.2a, you can model large-strain viscoelasticity besides linear viscoelasticity. See how to use this material model in a biomedical application.
The Mechanics of Arteries
Arteries are blood vessels that carry oxygenated blood from the heart throughout the body. They are layered structures consisting of intima, with media and adventitia (also called externa) on the outside layers. The media and adventitia are the layers that are primarily responsible for mechanical behavior in healthy arteries.
Both of these layers are made up of collagenous soft tissues that exhibit noticeable strain stiffening behavior. Each layer has anisotropic properties because of families of collagen fibers. This means that these fiber-reinforced structures allow the blood vessels to experience large strains.
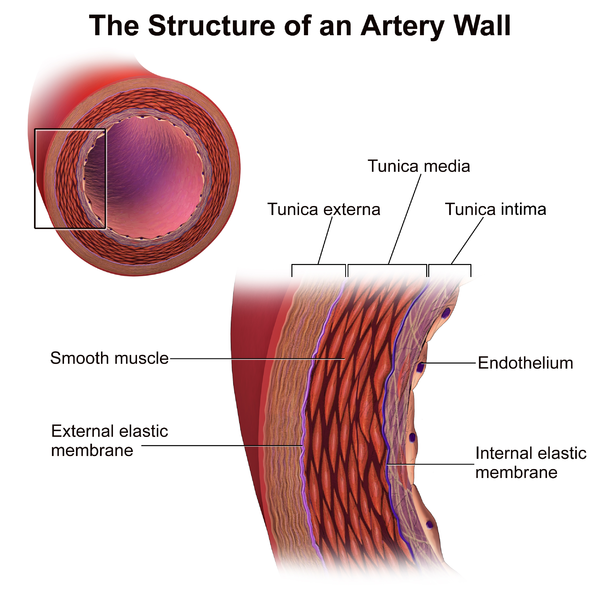
An artery wall’s structure. Image by BruceBlaus — Own work. Licensed by CC BY 3.0, via Wikimedia Commons.
A reliable constitutive model for arterial wall mechanics is essential to investigate changes in the arterial system due to age and disease, and for designing prostheses, among other uses (Ref. 3). The Holzapfel-Gasser-Ogden (HGO) constitutive model (Ref. 2) captures the anisotropic mechanical response described above, which has also been observed in lab experiments on excised arteries. Typical experiments in the lab measure the response of arterial sections subject to combined axial stretch and internal blood pressure, and numerical examples try to match this data to better understand its mechanics.
The Theory Behind Large-Strain Viscoelasticity
As Bower points out in Applied Mechanics of Solids: “Finite strain viscoelasticity is not as well developed as finite strain plasticity, and a number of different formulations exist.” In COMSOL Multiphysics version 5.2a, we implemented the Holzapfel model for large-strain viscoelasticity (Ref. 1, Ref. 3), which is well suited to combine with any of the predefined hyperelastic material models available in the COMSOL® software.
The author proposes a generalized Maxwell model based on the splitting of the strain energy density into volumetric and isochoric contributions
Here, stands for the right Cauchy-Green deformation tensor and
stands for its isochoric counterpart. The free energy associated to the nonequilibrium state,
, is a function of the isochoric right Cauchy-Green tensor
and internal strain-like variables
(Ref. 1, Ref. 3).
The strain energy in the pure-elastic branch is normally denoted with the superscript to denote the long-term equilibrium (as
).
Then, Holzapfel derives the expression for the second Piola-Kirchoff stress in the hyperelastic and viscoelastic branches
and also defines the auxiliary stress tensors from thermodynamic considerations
The total second Piola-Kirchoff stress (hyperelastic and viscoelastic branches) is then given by
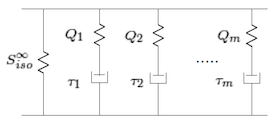
A schematic representation of the second Piola-Kirchoff stress for a generalized Maxwell model in large-strain viscoelasticity.
The evolution of the stresses in the viscoelastic branches is given by solving the rate equations
where is the relaxation time of the branch and
is the corresponding second Piola-Kirchoff stress tensor.
Holzapfel also assumes that there should be an isochoric strain energy density associated to the spring on each branch, , so
The main assumption in the Holzapfel formalism is that the isochoric strain energy per branch depends on the isochoric strain energy of the main hyperelastic branch
Here, the dimensionless coefficients are called strain energy factors.
The second Piola-Kirchoff stress per branch then becomes
and the rate to solve becomes
The generalized Maxwell viscoelastic model in version 5.2a of COMSOL Multiphysics is available for all of the hyperelastic materials, and it also contains the same options for modeling thermal effects as implemented for linear viscoelasticity.
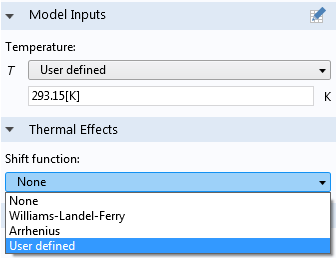
With the User defined option, you can neglect thermal effects, use the predefined William-Landel-Ferry or Arrhenius shift functions, or define your own shift function.
Let’s take a look at how large-strain viscoelasticity can be applied to biomechanics modeling.
Modeling Large-Strain Viscoelasticity in COMSOL Multiphysics
To model the behavior of arterial walls after sudden changes in axial stress, we need to use a hyperviscoelastic material model, which goes beyond the HGO material model.
Take a look at the Arterial Wall Mechanics tutorial model for more details on how to set up an anisotropic hyperelastic material.
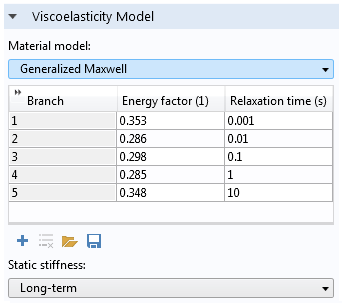
To start, let’s add viscoelastic behavior to this particular material model. As described in Ref. 3, a generalized Maxwell model of five branches added to the HGO model is suitable to model relaxation times ranging from 1 ms to 10 seconds. This model is suitable for quantitatively representing the viscoelastic response of circumferential segments of arteries (Ref. 3). To do so, we right-click on the Hyperelastic material node and add a Viscoelasticity node (we can also combine this with thermal expansion or other effects).
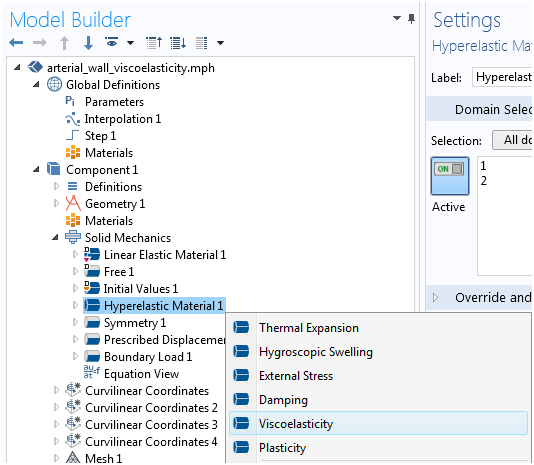
By default, we get a generalized Maxwell model with one branch. However, we can also use the standard linear solid (SLS) model or the Kelvin-Voigt viscoelastic model.
Then, we add the five branches with the corresponding energy factors and relaxation times as described in (Ref. 3). We are able to retrieve (and also save) such parameters from a text file.
After refurbishing the HGO hyperelastic material with five viscoelastic branches, we can simulate what happens in an artery section when subject to a constant axial strain for four minutes.
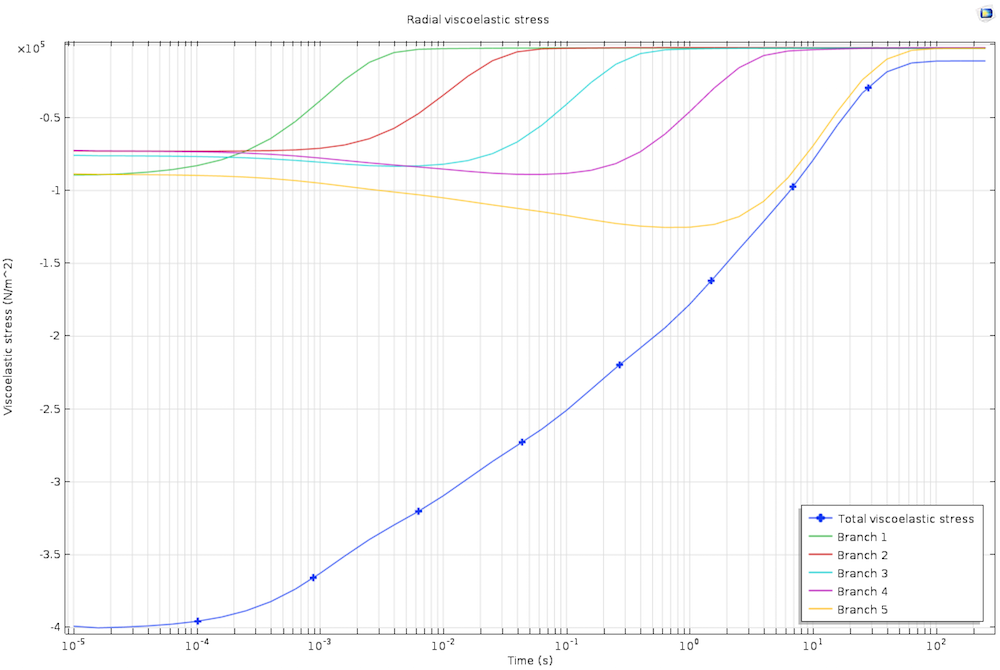
The stresses in the viscoelastic branches. Note the different relaxation times for the stresses in the five branches of the generalized Maxwell viscoelastic material.
The axial stress relaxes to the steady state for times longer than the highest relaxation time. The ability to model large-strain viscoelasticity in COMSOL Multiphysics enables us to easily investigate and understand different biomedical materials and applications.
Next Steps
- Try it yourself: Download the Arterial Wall Viscoelasticity tutorial model and related information
- See how linear viscoelasticity can be used to reduce vibrations in structural dampers
References
- G. Holzapfel, Nonlinear Solid Mechanics: A Continuum Approach for Engineering, John Wiley & Sons, 2000.
- G. Holzapfel, T. Gasser, and R. Ogden, “A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models,” J. Elasticity, vol. 61, pp. 1–48, 2000.
- G. Holzapfel, T. Gasser, and M. Stadler, “A Structural Model for the Viscoelastic Behavior of Arterial Walls: Continuum Formulation and Finite Element Analysis”, European Journal of Mechanics A/Solid, vol.21, pp. 441–463, 2002.



Comments (4)
damião costa
February 26, 2019How can I get the energy factors of a given material analytically?
Ed Gonzalez
February 27, 2019 COMSOL EmployeeHi Damiao, as done in small-strain viscoelasticity, the relaxation time and energy factor coefficients are determined with a regression method, where the analytical formula is fitted to lab data.
Greetings
Ed
Zihao Zhao
May 15, 2023How to concatenate Maxwell model and Kelvin Voigt model in a linear elastic material?
Ed Gonzalez
May 16, 2023 COMSOL EmployeeHi Zihao,
You just need to add two Viscoelasticity nodes to a Linear Elastic Material. Then, adjust in one node the settings for the Maxwell model, and in the other node enter the material parameters for the Kelvin-Voigt model.