
Picture this: A chain of red ants crawl along the surface of a yellow loop. Although the ants appear to be on a two-sided surface, the loop is actually a one-sided surface. Sound familiar? It’s the design featured on the famous wood engraving Möbius Strip II by Dutch artist Maurits Cornelis (M.C.) Escher. As indicated by the artwork name, the object that the ants are crawling on is called a Möbius strip. Since 1858, the year of its discovery, this unusual object has amazed mathematicians and artists alike. In this blog post, we discuss the origin of the Möbius strip, how to easily make one, and the many practical uses of it.
A Tale of Two Mathematicians: Discovering the Möbius Strip
August Möbius
Born in Schulpforta, Saxony (Germany), on November 17, 1790, August Ferdinand Möbius showed an early interest in mathematics. He was homeschooled until age 13 and later attended the College of Schulpforta, graduating in 1809. Continuing his education, he went on to attend the University of Leipzig, where he studied mathematics, astronomy, and physics. His astronomy teacher, Karl Mollweide, known for the discovery of the Mollweide trigonometric relations and the Mollweide map projection, was his biggest influence.

Portrait of August Ferdinand Möbius. Image in the public domain, via Wikimedia Commons.
From 1813 to 1814, Möbius attended the University of Göttingen, where he studied astronomy under Carl Friedrich Gauss, one of the most influential mathematicians of all time. After attending the University of Göttingen, Möbius went on to study mathematics under Johann Pfaff, a teacher of Gauss, at the University of Halle. By this time, Möbius was well versed in both astronomy and math.
In 1816, Möbius returned to the University of Leipzig as the chair of astronomy and higher mechanics. From 1818 to 1821, he watched over the construction of the university’s observatory, later becoming its director in 1848.
Throughout his career, Möbius published several important works on astronomy, including:
- Concerning the Calculation of the Occultations of the Planets (1815)
- The Principles of Astronomy (1836)
- The Elements of Celestial Mechanics (1843)
He also published well-known texts in the field of mathematics, including the Calculus of Centres of Gravity (1827), which covered projective and affine geometry, and the Textbook on Statics (1837), which discussed the geometric treatment of statics.
Möbius’ name lives on in a variety of mathematical concepts, such as the Möbius function in number theory, Möbius plane, and Möbius transformations. However, he is best remembered for a discovery he made in 1858. In a memoir, posthumously presented to the Académie des Sciences, Möbius discussed his finding of the Möbius strip: a single-sided surface with only one boundary. He made the discovery while working with polyhedra, solid figures composed of flat faces, straight edges, and sharp vertices. The Möbius strip, also known as the Möbius band, helped develop the field of topology.
Johann Benedict Listing
Although the Möbius strip is named after August Möbius, this unique surface was simultaneously and independently discovered by German mathematician Johann Benedict Listing.
Listing was born in Frankfurt, Germany, on July 25, 1808. Like Möbius, Listing grew up with a strong appreciation for mathematics, attended the University of Göttingen, and studied under the great mathematician Gauss. Through the teachings of Gauss, Listing gained an interest in topological ideas, on which he published several papers throughout his life. In fact, Listing’s 1847 book Introductory Studies in Topology is often cited as the first published use of the term topology.

Johann Benedict Listing. Image in the public domain, via Wikimedia Commons.
Listing first documented his discovery of the Möbius band in his notes from 1858. He later published his description of the band and its properties in 1861.
Today, it is widely accepted that Möbius and Listing independently discovered the band, but some people theorize that it was actually Gauss who found it, and it was he who passed the idea of the strip on to both Möbius and Listing.
A Simple Visualization of a Möbius Strip
You don’t need to be M.C. Escher to make a Möbius strip: You can easily create one using a rectangular piece of paper, a stapler (or some type of adhesive), a writing utensil, and scissors. We tried it and it worked:
In this video, see how to create a Möbius strip. Note that when the Möbius strip is cut in half, the resulting strip is no longer a Möbius band but homeomorphic to a cylinder.
Möbius Strips Are All Around Us
From machines and tools to logos and symbols, we likely encounter many one-sided surfaces everyday. Let’s take a look at a few common (and less common) uses of Möbius strips…
Tools and Instruments
Conveyor belts were once manufactured as Möbius strips, which allowed the whole surface of the belt to receive an equal amount of use, so that it would last longer. However, Möbius strip conveyor belts are less common today because more durable untwisted belts can be made by combining a variety of materials.
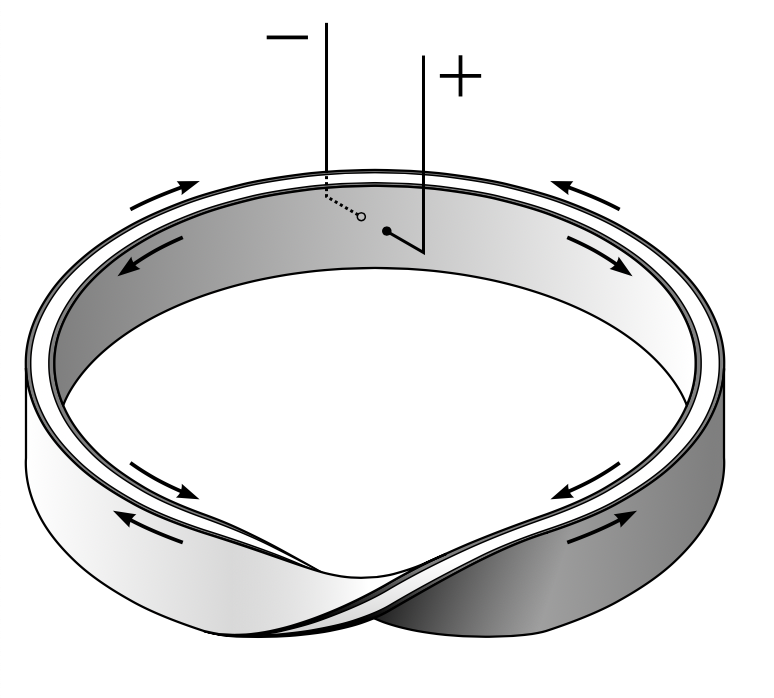
A diagram of the current flow in a Möbius resistor. Image by Ilmari Karonen. Image in the public domain, via Wikimedia Commons.
In the 1960s, the Möbius strip was used in the design of a noninductive electrical resistor. The patent for this design, filed by Richard L. Davis of Sandia Laboratories, reads: “This invention contemplates utilizing insulated resistive material in the form of a Möbius surface with electrical leads attached diametrically opposite each other to the resistive material as a noninductive resistor.” A noninductive resistor of this kind is inexpensive to produce, has neither residual inductance or mutual inductance, and is nonreactive at high frequencies.
A few other practical applications of Möbius strips include:
- Continuous-loop recording tapes
- Typewriter ribbons
- Computer print cartridges
Art
Thanks to its unique, eye-catching appearance, many artists use the Möbius strip as inspiration for their artwork. It is found in paintings, animations, sculptures, and more. Swiss artist Max Bill is considered a pioneer of using the Möbius band in art. His 1935 granite sculpture Endless Ribbon is one of his more popular works featuring the band. When Bill first started incorporating the Möbius strip into his artwork, he thought he was the originator of the surface. However, he soon learned that the Möbius strip had been named for many decades. He continued to find inspiration in math for his future pieces.
Below, you can see the Ring of Möbius designed by Möbius himself and completed by ing. Hans Kalkhoven in 1986. The sculpture can be found at the Eindhoven University of Technology.

Ring of Möbius designed by August Möbius and completed by ing. Hans Kalkhoven. Image by Alex P. Kok, licensed under CC BY-SA 4.0, via Wikimedia Commons.
More recently, in August 2021, Mamma Mobius, a 4-ton sculpture by artist Mark Du Suvero, was installed at the San Luis Obispo Museum of Art in California. As its name suggests, this sculpture pays homage to the Möbius strip.
The three examples described here are just a few of the many ways in which the Möbius strip finds its way into the world of art.
Nature
Does this rock formation look familiar? Its arch is in the shape of a Möbius strip, hence why it’s called the Mobius Arch. This major tourist attraction is located in Inyo County, California. If you look closely, you’ll see that its window frames Mount Whitney!

Mobius Arch. Image in the public domain in the United States, via Wikimedia Commons.
The sightings of this one-sided object don’t end in nature — It can also be found in architecture; jewelry; logos; and symbols, such as the universal recycling symbol.
2 Examples of Modeling a Möbius Strip
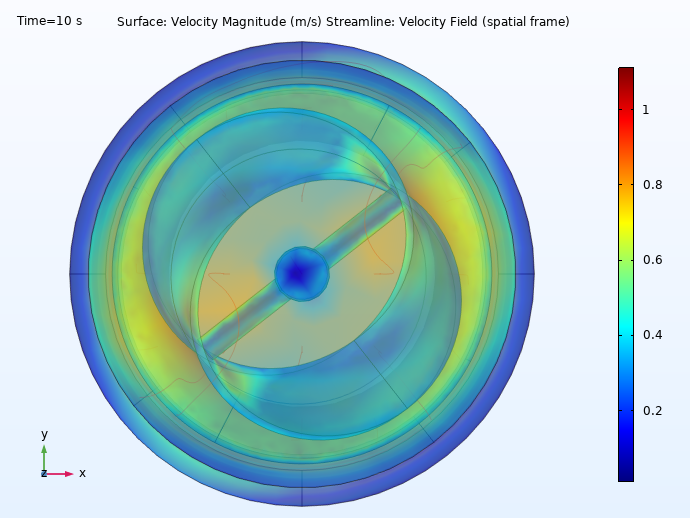
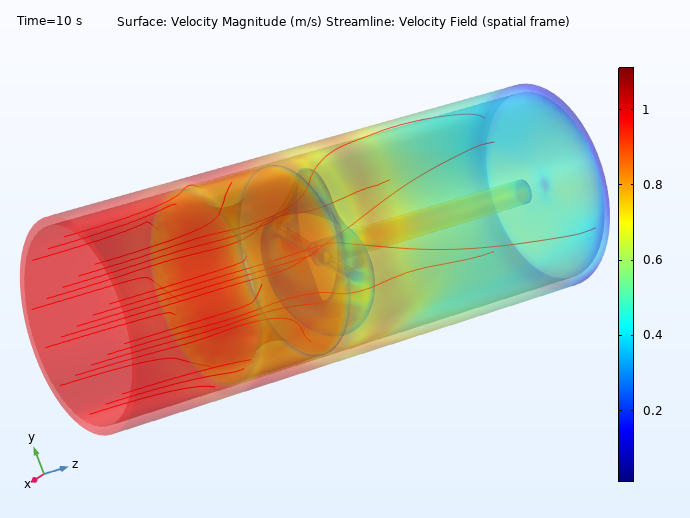
Gas meters measure the amount of fuel gases delivered through a pipeline in residential, commercial, and industrial buildings. Raychem RPG, a leading provider of domestic gas meters in India, developed a turbine meter with a Möbius-band-shaped rotor. In this type of gas meter, the gas flow rate is measured by the turbine’s rotation and the gas volume is determined by the velocity of the gas moving through the Möbius strip.
The Raychem team used multiphysics simulation to analyze the performance of their design:
Two different angles showcasing the velocity profile of the flowing gas in Raychem RPG’s Möbius band flowmeter.
Another example: In April 2021, researchers from the United Kingdom shared how they designed a Möbius strip resonator and used simulation to analyze its radar cross section (RCS), scattering cross section (SCS), absorption cross section (ACS), and angular response. They released their findings in a paper published in Scientific Reports.
Concluding Thoughts
Unlike the Möbius strip, this blog post has come to an end. Here, we’ve gone over the history of this one-sided band, how to make one by following a few simple steps, and the many ways in which this object is present in the world around us.
Further Reading
- Learn more about the Möbius strip through these resources:
- Read more about the field of mathematics launched by the Möbius strip, topology, on the COMSOL Blog:





Comments (2)
Ivan Colorado
November 26, 2021Hi Rachel,
Thanks for sharing this nice blog. Me and my colleges are working in the stress-free morphing of flat sheets into complex three-dimensional geometries. We are able to homeomorph an initially flat parallelepiped of dimensions [L x W x H] into a Möbius strip by prescribing a target metric. We would be happy to share with you our simulations.
Rachel Keatley
December 3, 2021Hi Ivan,
Thank you for your comment! I will contact you via email to learn more about your work.