
In gaseous photoacoustic spectroscopy, light and sound are used to detect concentrations of hazardous compounds in the surrounding environment. Compared to other spectroscopy techniques, photoacoustics shows the highest signal-to-noise ratio due to its detection scheme — but because the generated sound wave is often too weak to be detected by a microphone, an acoustic cell is used to amplify the signal. Researchers at Imec and KU Leuven are working to increase the sensitivity of this acoustic cell via topology optimization.
What Is Photoacoustic Spectroscopy?
Back in 1880, Alexander Graham Bell was working on the photophone, a device that uses modulated light to transmit speech wirelessly. In the process, he discovered the photoacoustic effect. Bell was able to demonstrate this phenomenon by exposing thin discs to sunlight. As chopped light would repeatedly heat the discs, they would emit sound. In other words, thermal expansion occurred, which would generate a pressure wave. Later, Bell showed that materials exposed to ultraviolet and infrared radiation also produce sound. While the photoacoustic effect was of interest to the scientific community at the time, there wasn’t much use for it until about a hundred years later.
Nowadays, the effect is used as a measurement technique known as photoacoustic spectroscopy, and there have been some updates to the technology involved. For example, instead of waiting on beams of sunlight, it’s much more effective to use a laser. Likewise, advances in electronics and manufacturing techniques have made it possible to expand use cases for this process, as well as the accuracy and sensitivity of detection.
How Does Photoacoustic Spectroscopy Work?
Photoacoustic spectroscopy is a measurement of the effect of absorbed light on matter via acoustic detection. Because it is called a “zero background technique”, the sensitivity achieved allows you to study concentrations of analytes in gas down to the part-per-billion- and trillion-level ranges. Here’s how it works:
- An analyte is dissolved in a buffer gas, such as air, nitrogen, or a noble gas
- The gas flows in a chamber or cell
- An intensely modulated laser beam also propagating within the cell excites the analyte once its wavelength corresponds to one of the analyte’s absorption peaks
- Repetitive generation of heat from this absorption causes a pressure wave in the gaseous medium
- The pressure wave is detected by a microphone in the cell setup
- The wavelength of the laser and recorded sound intensity identify the analyte and measure its concentration
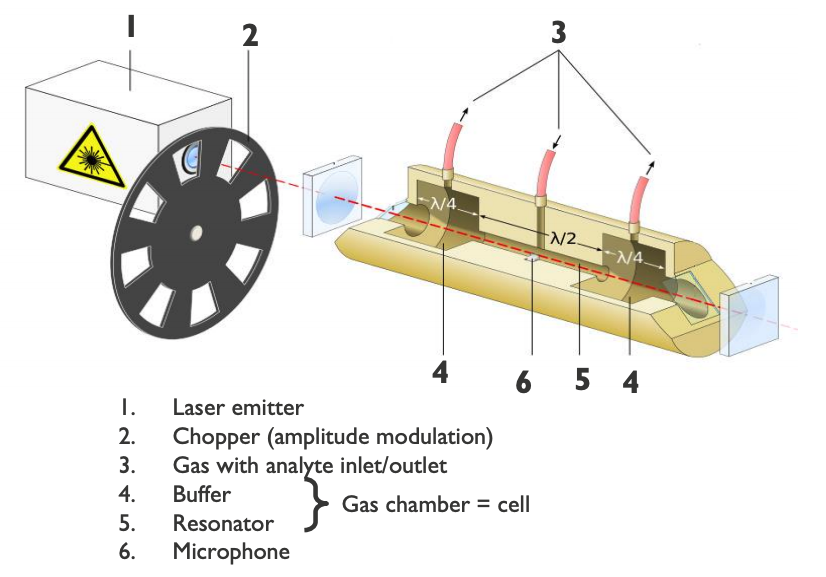
Schematic of a gaseous photoacoustic spectroscope. Background image by Hk kng — Own work. Licensed under CC BY-SA 3.0, via Wikimedia Commons.
The sound wave in this type of setup is usually pretty weak, so the sound can be amplified by choosing a frequency modulation of the laser equal to the natural frequency of the cell, which also serves as an acoustic chamber. Placed strategically, the microphone can better pick up this signal.
Many engineers focus on designing a more sensitive microphone, but until now, not as much attention has been paid to the acoustic cell (or chamber). Recently, due to fewer manufacturing limitations and new technology like 3D printing, it’s possible for researchers to decrease the size of the cell to make it more sensitive. In addition, topology optimization techniques have improved due to increasing computational power, thus making it possible to change the shape of the cell.
Researchers at Imec and KU Leuven decided that with these advances, it was time to focus on designing an improved acoustic cell. Using the COMSOL® software, they were able to investigate the topology optimization of a 3D-printed acoustic chamber for gaseous photoacoustic spectroscopy. They presented their findings at the COMSOL Conference 2017 Rotterdam.
Modeling an Improved Acoustic Cell with COMSOL Multiphysics®
The researchers began their investigation into optimizing gaseous photoacoustic spectroscopy by thinking about various ways the acoustic cell could be improved. They chose topology optimization as the “freest option.” Rachid Haouari of Imec explains that while they could have used a more general shape optimization, the final shape would “always be dependent on the function basis” that is picked up, and a “shape with fine features requires a big basis set in order to render high spatial frequencies.” Although he notes that the final topology should be able to be manufactured and therefore have some typical constraints, topology optimization presented the best option for being relatively constraint-free.
The main constraints they found for the topology optimization setup were having a limited amount of material available and needing the cell to be light due to its size, so they began defining the shape as an optimized distribution of a material property. They also set up penalized functions such as penalized damping, or “pamping,” to account for the acoustical impedance mismatch. Because the mismatch is high enough to safely assume that there’s no transfer from gas to solid, pamping was applied in the solid areas to ensure sound wouldn’t travel there.
For more information on the functions and constraints used in this research, refer to the technical paper.
Setting Up the Acoustic Chamber Geometry
In an acoustic chamber, the lossless propagation of a sound wave in a medium is governed by the Helmholtz equation. To implement this in the COMSOL Multiphysics® software, the researchers used the Pressure Acoustics, Frequency Domain interface in the Acoustics Module. Their aim was to maximize the retrieved sound pressure intensity at the microphone location and at one desired frequency.
As shown in the schematic below on the left, the laser beam is simplified to a linear sound source. Paths were set as plain air for the laser area (shown in green) and the connection tunnel between the cell and microphone. The gray area is the main area that undergoes topology optimization. The microphone is assumed to be circular and its position can be set where desired.
Using COMSOL Multiphysics and a combination of the Acoustics Module and the Optimization Module, the research team was able to implement their optimization scheme with key variables and parameters, including the “pamping” function mentioned previously. The resulting 3D geometry (shown below on the right) is a cube with a horizontal cylinder representing the laser beam, and the axis is the linear sound source. A vertical cylinder above the microphone is filled with air to ensure an acoustic path. The green area is the optimized topology zone.
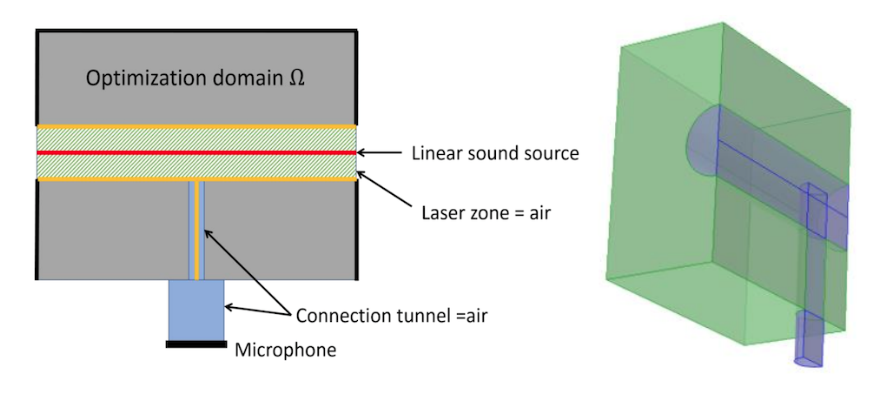
Schematic of the acoustic cell optimization geometry (left). 3D geometry of the acoustic cell (right). Images courtesy Imec/KU Leuven.
The volume of the cube was set to 1 cm3, and the frequency was set to a low 25 kHz so that the signal would be high. This frequency is out of the audible range, and therefore free from most acoustic pollution. Poly(methyl methacrylate) (PMMA) was set as the solid, with a density of 1180 kg/m3 and sound speed of 2500 m/s.
Small “Potatoes” with Big Results
Finding Optimal Placement Within the Chamber
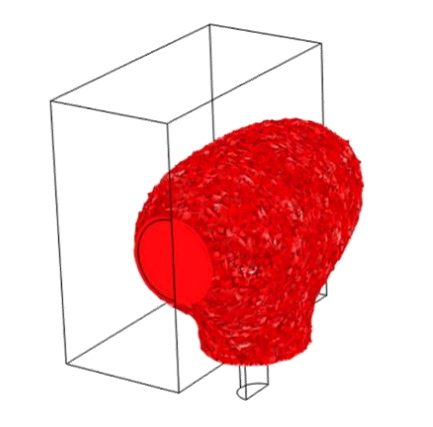
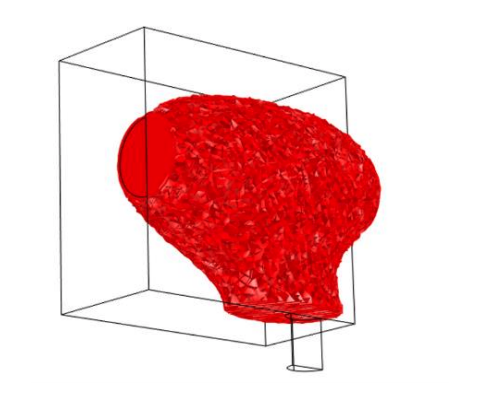
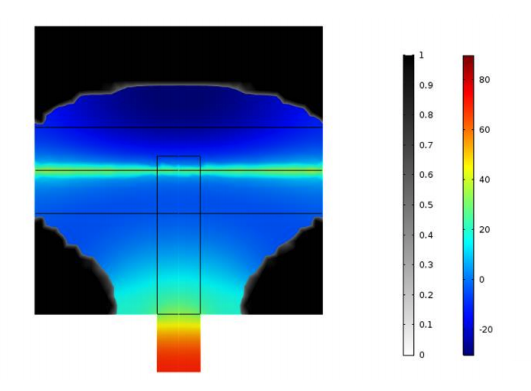
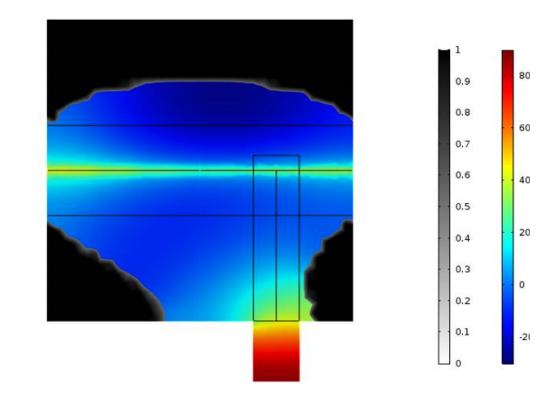
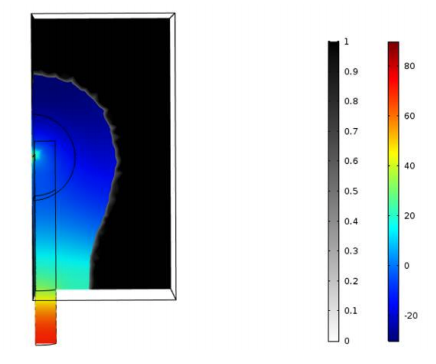
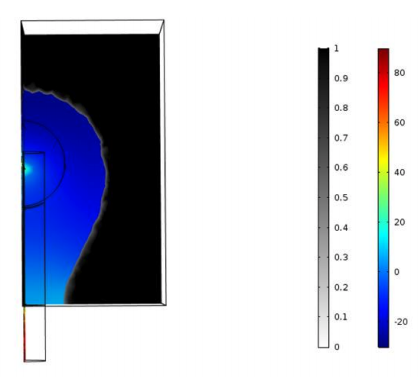
First, the research team ran several simulations where they changed the position of the microphone in order to study the resulting shapes around the laser beam. They noticed that the main shape around the laser beam remained about the same for each simulation, which they describe as a “potato”-shaped ellipse. This potato shape presents the same revolution symmetry around the laser beam, as we can see in the results below. The only visible difference is around the microphone location, where there is a collector that concentrates sound waves into the tunnel. The researchers noticed that the opening of the collector depends on the wavelength.
|
|
|
|
|
|
Left column: The optimized shape with the microphone location at the center. Right column: The optimized shape with the microphone location shifted from the center. Images courtesy Imec/KU Leuven.
For both microphone placement locations, the color represents the pressure amplitude while the black and white (set to transparent) represent the presence of the material. For a sound wave input power of 10-5 W, they retrieved a 71-Pa pressure average on the microphone at the center location and an 86-Pa pressure average on the microphone at the shifted location. These pressure response findings revealed that the photoacoustic cells are equivalent if they have the same:
- Volume
- Laser path length
- Buffer gas
- Absorbed laser power
The rest is shape dependent!
Comparing the Photoacoustic Performance in 2 Cell Shapes
Moving on with confidence in the topology optimization, the research team considered the surface geometry of the cell. Haouari says that one of the challenges of making the acoustic chamber smaller is that as the cell size decreases, the degradation of the amplification ability increases. He says that this is mainly due to the ratio of thermoviscous losses “at the surface” over “in volume” — so the surface geometry is important for small cells. To solve this issue, the team used the Thermoviscous Acoustics, Frequency Domain interface to account for thermal and viscous losses.
To address the surface problem, Haouari explains that this is where simulation software “takes the lead, since resolution of this kind of problem is almost impossible to do by hand.” The multiphysics capabilities COMSOL® software, says Haouari, did so with “panache.”
The problem was addressed by exporting function data for the optimized shape into the MATLAB® software in order to retrieve the surface needed. Then, the researchers reimported the surface into the COMSOL Multiphysics® software as a 3D geometry, and, using the thermoviscous acoustics features, defined boundary layers on the surface and a modulated heat source, thus simulating the photoacoustic effect.
Finally, the team compared the final photoacoustic performance of the optimized potato shape to that of a cylinder. They found that the optimized cell does, in fact, achieve higher amplification at its resonance compared to the cylindrical shape. In the frequency response graph, depicted below, it is seen that the potato shape has a resonance frequency of 24 kHz while the cylinder has its first resonance at 30 kHz. It is also seen that the potato shape is capable of providing twice the output pressure of the cylindrical cell (notice the logarithmic scale) at resonance.
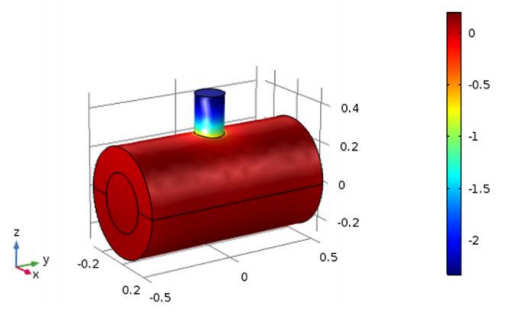
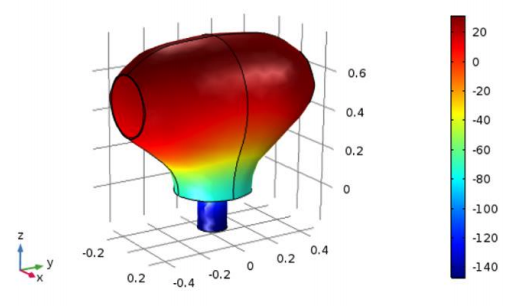
Simulated pressure repartition at 25 kHz on a conventional cylinder (left) vs. the team’s potato-shaped cell (right). Images courtesy Imec/KU Leuven.
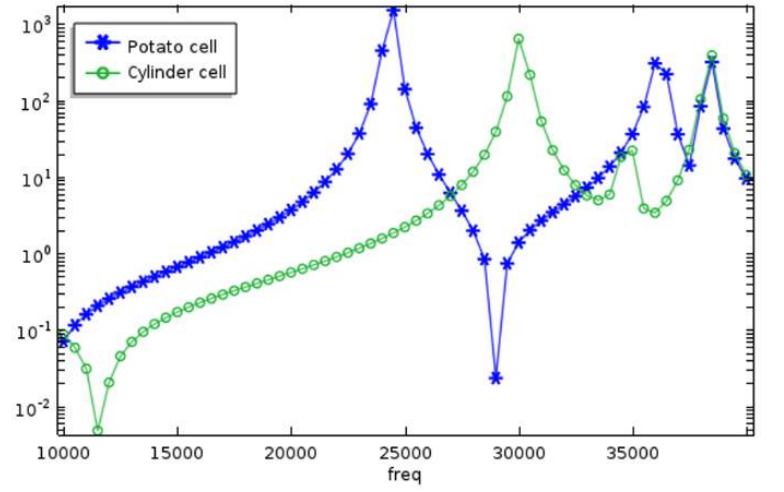
The frequency response of the cylindrical acoustic chamber (green) and potato-shaped chamber (blue) from 10 to 40 kHz. Image courtesy Imec/KU Leuven.
The reason the potato shape is able to provide higher amplification is due to the lower losses at the cell walls. Since, when we look at a cross section of the cell, the upper part of the shape is circular, the sound emitted by the laser can be seen as a point source at the center of the circle and is able to propagate with radial waves. A radial wave interacting with a circular wall won’t generate any friction; therefore, no losses will occur.
After confirming that the optimized shape is able to provide greater amplification, the Imec and KU Leuven team has been working on an experimental setup and protocol to continue to assess the signal improvement. Haouari says that this setup will be integrated in a “novel, gaseous-phase-, cell-based, miniaturized photoacoustic spectroscopy setup” in the hopes of increasing the sensitivity of the acoustic cell.
Learn More
- Get more details on Imec and KU Leuven’s research by reading the conference paper: “Topology Optimization of a Gaseous Photoacoustic Spectroscopy Cell Using COMSOL Multiphysics®“
- Read this blog post on how to use topology optimization results as model geometries
- Try these related tutorial models:
MATLAB is a registered trademark of The MathWorks, Inc.






Comments (0)