
How Well Do Mosquito Traps Work? Observing Their Effectiveness with Particle Tracing
When the weather is nice and warm, nature attracts adrenaline-seeking hikers and happy campers alike. However, where there is vegetation, there are also mosquitoes waiting to find their next target. So what’s a camper to do? Mosquito traps can be effective, so long as mosquitoes find them more appealing than any nearby sources of blood. For fun, let’s turn to equation-based modeling to see if a camper’s trap will keep his cabin in the woods cozy and mosquito-free — or if the insects will kill the camping buzz.
Mosquito Magnets: Carbon Dioxide and Lactic Acid
There are various reasons why female mosquitoes are drawn to humans and animals. (Why female, specifically? Because only female mosquitoes consume blood, as they need the protein found in blood to produce eggs.) According to the National Environment Agency, different species of mosquitoes are more susceptible to certain attractants, hence why many commercial mosquito traps use different attractants in combination.
Visual cues (such as movement) and thermal cues (such as body heat) play a part in attracting female mosquitoes to blood sources, but a large portion of the draw-in comes from scent. Mosquitoes can be drawn in by carbon dioxide; lactic acid, a chemical compound in human sweat; and certain pheromones, to name a few. Using these scents as bait in a mosquito trap can help increase the trap’s effectiveness.

A mosquito on a leaf. Photo by Syed Ali on Unsplash.
Armed with a basic understanding of what mosquitoes find irresistible and simulation software equipped with equation-based modeling and particle tracing functionality, let’s see how well a simple mosquito trap performs at attracting these little menaces.
Modeling a Mosquito Trap in a Cabin
To perform equation-based modeling, we will take advantage of two aspects of the COMSOL Multiphysics® software: a selection of Mathematics interfaces as well as a feature that interprets mathematical equations added by the user and incorporates them when generating a numerical model.
When modeling a mosquito trap, we need to consider what mathematical equations describe mosquito flight. One way to go about this is to describe an attractor concentration with the Laplace equation. The model in our example here solves the Laplace equation for a velocity potential, which is designed to be proportional to the concentration of a general mosquito attractor. The velocity potential represents all molecules that may attract mosquitoes, including carbon dioxide and the scent emitted from the trap.
Blissfully Asleep
To better visualize this model scenario, let’s bring back our camper and suppose that he is staying at a cabin in the woods. It’s a warm night, so to sleep comfortably he decides to open the window. He sets up a mosquito trap above the bed and figures it should keep him safe. According to the manufacturer, the trap is supposed to be 60% more appealing than a real blood source and he opts to take his chances.

A model of a cabin with an open window, a person sleeping, and a mosquito trap on the shelf above their bed.
Uh-oh! Our camper made a miscalculation: he moves around in his sleep. As he is dreaming of next morning’s scenic hike, he moves around and so does the blanket, leaving parts of his torso and legs uncovered. Next, a swarm of mosquitoes fly in through the open window and they are looking for blood. They can either go for our camper or the mosquito trap. Will he be safe or wake up itchy?
Path of Attack
To determine where the mosquitoes will go, we need to add certain equations to the model. In this example, Dirichlet Boundary Condition features are added to three boundaries: the open window, the mosquito trap, and the camper’s exposed skin. Since the trap is supposed to be more of an attractant than the human skin, different velocity potentials are assigned to the trap and skin to represent this contrast.
We will also make use of the Particle Tracing Module, an add-on product to COMSOL Multiphysics, for our example. Of course, users of this module generally don’t model exaggerated scenarios like our mosquito swarm; more typical examples are to model particles that represent ions, cells, water droplets, planets or stars, and the like. In our playful example, though, each particle represents a mosquito. The Particle Tracing Module also includes functionality for solving user-defined equations of particle motion, which we use here to account for the motion of the mosquitoes in the cabin. The model is set up to count how many particles arrive at a point — in this case, at the skin versus the trap — at a select time.
Let’s see what happens:
The model when mosquitoes arrive in the room. Each black dot represents a mosquito. The red line represents the path of one mosquito to visualize its behavior.
Mosquito Trap vs. Human Skin: Which Do Mosquitoes Prefer?
After the model is set up and solved, we can plot the results and compare how many mosquitoes arrived at our poor camper’s skin versus the trap over a time frame of 150 seconds, or 2.5 minutes. As shown below, the number of mosquitoes landing on the skin over time increases — this is partially due to the fact that the camper is closer to the open window than the trap is. However, the number of mosquitoes that land on the trap also increases, overpassing the number of those landing on the skin at about the halfway point of the given time frame.
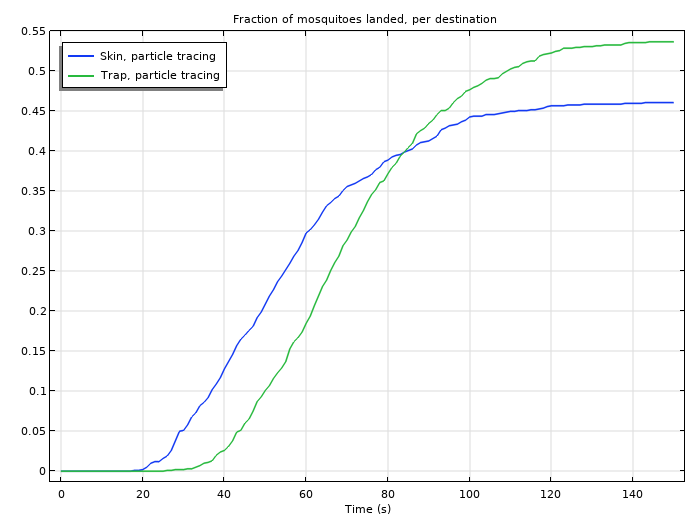
A graph comparing the number of mosquitoes that land on the skin versus the trap over a time frame of 150 seconds.
In other words, he was better off with the mosquito trap than without it and the (fictional) manufacturer was honest about the intended performance. With the use of the software’s equation-based modeling functionality, we were able to solve custom equations and analyze the relationship between mosquito behavior and a mosquito trap — all without bug bites!
More Buzzworthy Content
- Continue to explore the benefits of equation-based modeling with the following resources:
- Get a more detailed look at the use of the Mathematics interfaces for setting up the mosquito trap example by watching this webinar recording: Introduction to Equation-Based Modeling with COMSOL®
- Check out this 11-part, self-paced course on equation-based modeling with COMSOL Multiphysics®, highlighting partial differential equations (PDEs): Modeling with Partial Differential Equations in COMSOL Multiphysics®
- Check out these blog posts, which explore the scientific behavior of other insects:



Comments (0)