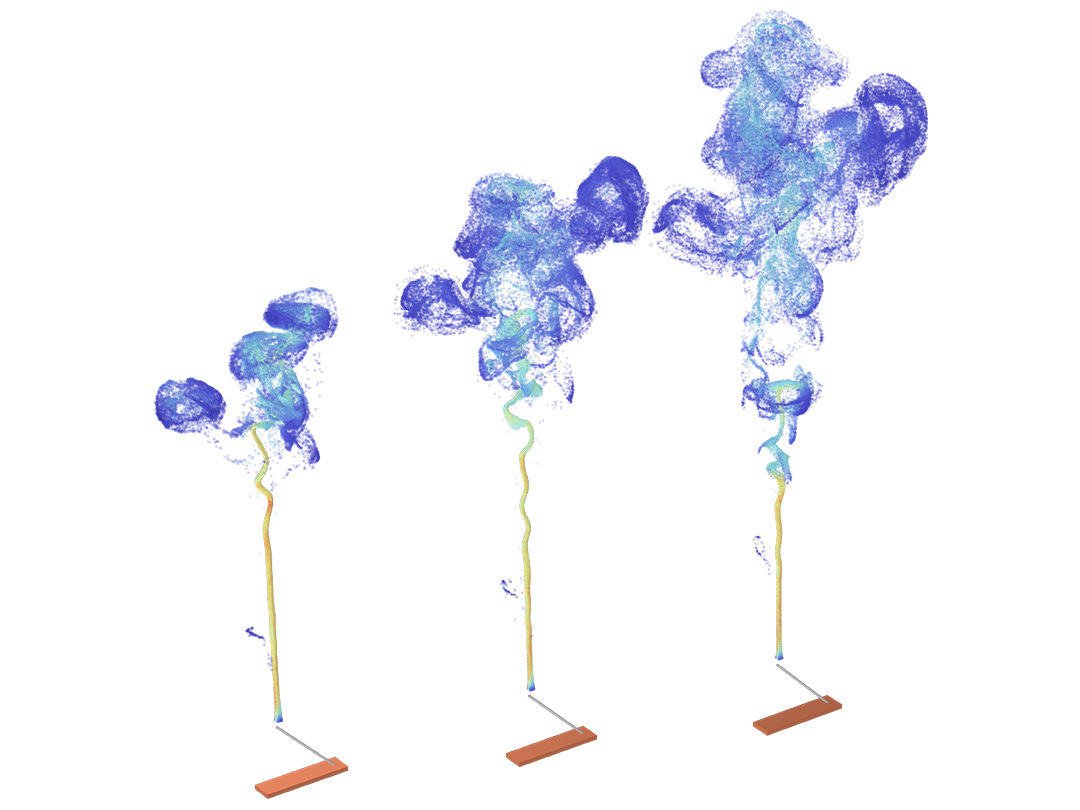Menu

Particle Tracing Module

Verfolgen Sie geladene Teilchen und Partikel in Strömungen

Particle Tracing (Partikelverfolgung) ist eine numerische Methode zur Berechnung der Trajektorien einzelner Partikel durch Lösen ihrer Bewegungsgleichungen über die Zeit. Im Gegensatz zu vielen anderen Methoden, die in der COMSOL Multiphysics® Software verwendet werden, wird beim Particle Tracing eine Reihe von diskreten Trajektorien gelöst und nicht ein kontinuierliches Feld.

Die simulierten Partikel können Ionen, Elektronen, biologische Zellen, Sandkörner, Geschosse, Wassertröpfchen, Blasen oder sogar Planeten oder Sterne darstellen. Je nachdem, welche Art von Teilchen modelliert wird, können Sie aus einer Vielzahl implementer Kräfte wählen, die ihre Bewegung beeinflussen. So können Sie beispielsweise vorhersagen, wie sich Elektronen in elektrischen und magnetischen Feldern bewegen oder wie sich Staub aufgrund der Schwerkraft und des Luftwiderstands absetzt. Sie können auch die anfängliche Position und Geschwindigkeit freigesetzter Partikel steuern und festlegen, was mit den Partikeln geschieht, wenn sie auf Ränder in der Geometrie treffen.

COMSOL kontaktieren
Ein Mischermodell, das die Trajektorien der Partikel in der Rainbow-Farbtafel zeigt.
Elektronentrajektorien, die durch drei graue Elektroden und die sie umgebenden Isoflächen des elektrischen Potentials in der Aurora Australis-Farbskala verlaufen.

Geladene Teilchen verfolgen

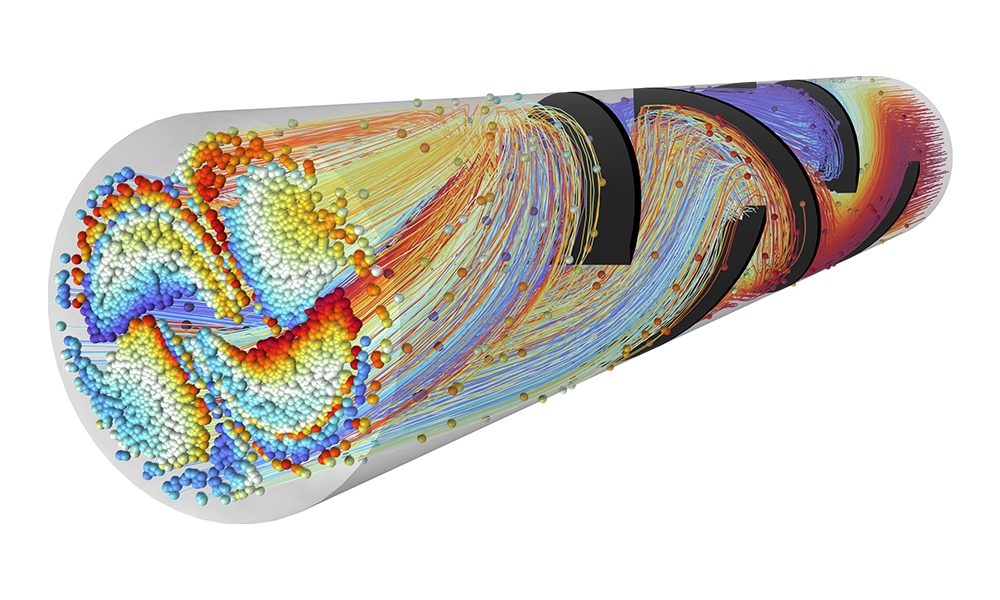
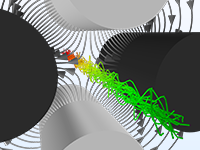
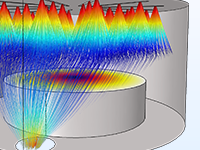
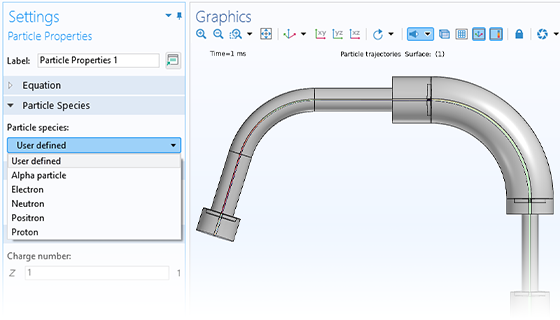
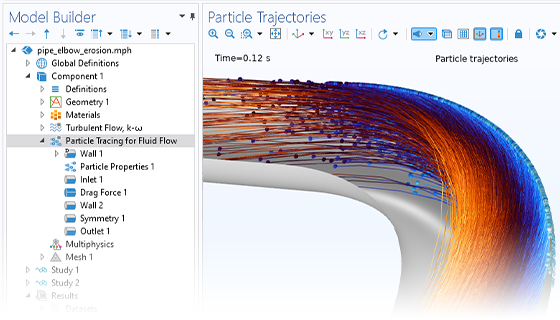
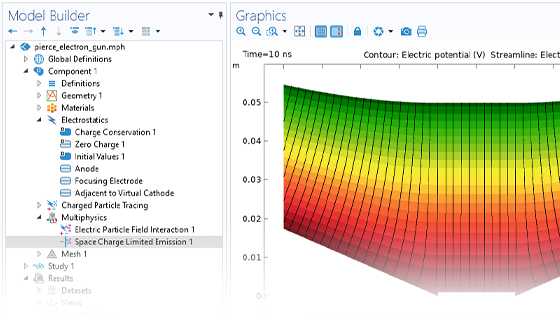
Die genaue Vorhersage der Bewegung von Ionen oder Elektronen in angelegten Feldern (Charged Particle Tracing) ist für die Konstruktion von Spektrometern, Elektronenkanonen und Teilchenbeschleunigern unerlässlich. Die angelegten Felder können benutzerdefiniert sein oder aus einer früheren Analyse stammen. Solche Felder können stationär, zeitabhängig oder im Frequenzbereich gelöst sein. Sie können eine beliebige Anzahl verschiedener Felder anwenden, so dass Sie stationäre und zeit-harmonische Felder in derselben Simulation überlagern können.

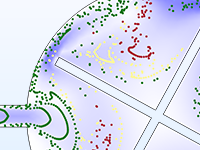
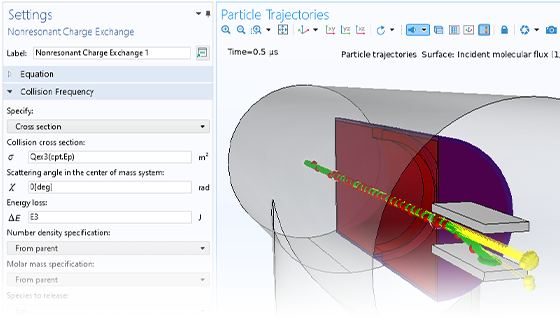
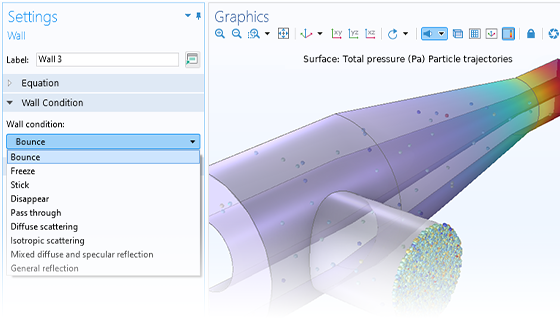
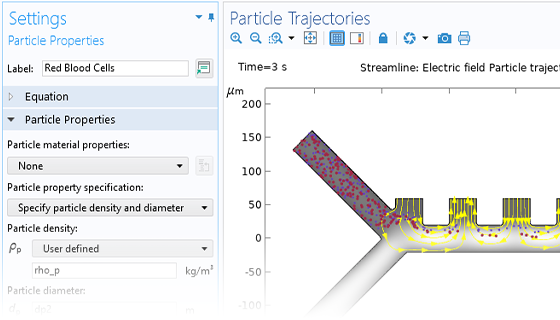
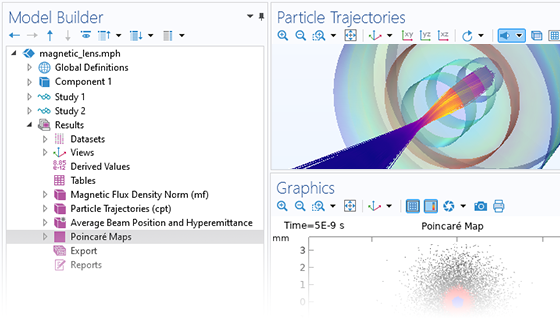
Die Teilchenbewegung findet selten in einem perfekten Vakuum statt. Sie können jedes Particle Tracing-Modell in ein Monte-Carlo-Stoßmodell umwandeln, indem Sie den Teilchen eine gewisse Wahrscheinlichkeit geben, mit den Molekülen des umgebenden Gases zu stoßen. Dies kann dazu führen, dass die Teilchen ihre Richtung ändern oder sogar Reaktionen wie Ionisierung und Ladungsaustausch durchlaufen.

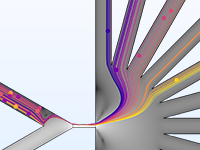
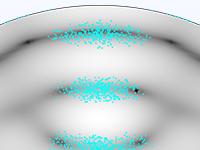
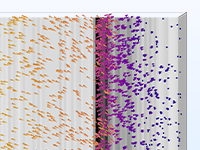
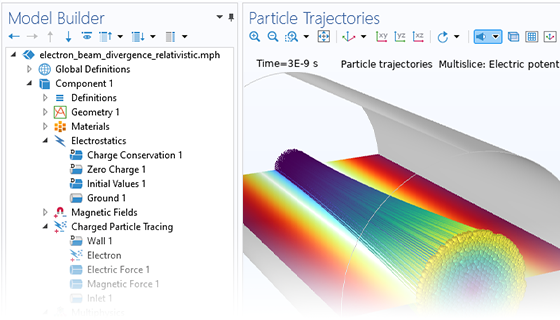
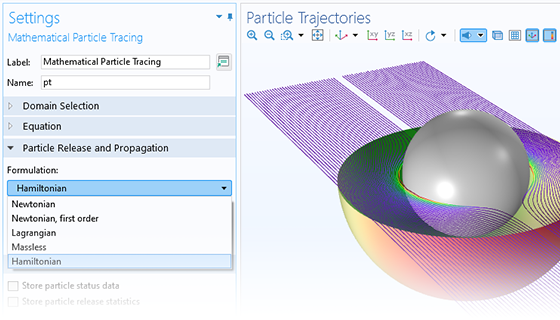
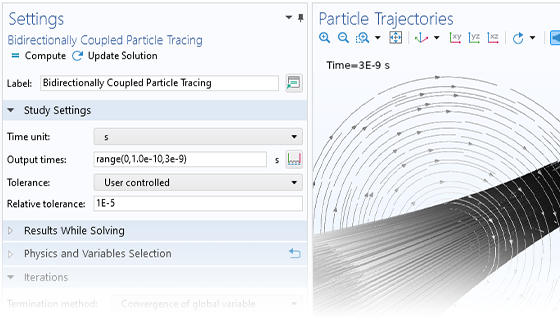
Die einfachsten Modelle zum Verfolgen geladener Teilchen beinhalten eine unidirektionale (Einweg-) Kopplung, bei der die Felder gelöst und dann zur Definition der Kräfte auf die Teilchen verwendet werden. Wenn sich die geladenen Teilchen in einem Strahl mit ausreichend hoher Stromstärke befinden, kann es notwendig sein, die bidirektionale (Zweiwege-) Kopplung zu berücksichtigen, bei der die Teilchen das Feld stören können. Es stehen vordefinierte Analysetypen zur Verfügung, um bidirektional gekoppelte Modelle bequem aufzusetzen.

Partikel in Strömungen verfolgen

Dispersion und Verdunsten von Tröpfchen in der Luft, das Wandern biologischer Zellen in einem Lab-on-a-Chip-Gerät und die Auswirkungen von Sedimenten auf die Wände von Öl- und Gaspipelines sind alles Beispiele für die Verfolgung von Partikeln in einer Strömung (Particle Tracing for Fluid Flow).

Für Partikel in einem Fluid sind die wichtigsten Kräfte oft der Luftwiderstand und die Schwerkraft. Je nach Anwendung können noch weitere Kräfte wie elektrische, magnetische, thermophoretische und akustische Strahlungskräfte hinzukommen. Die Partikelbewegung kann eine Zufallskomponente enthalten, wenn das Fluid turbulent ist oder wenn die Partikel so klein sind, dass die Brownsche Bewegung von Bedeutung ist.

Die Partikel können alle gleich groß sein, oder eine Größenverteilung aufweisen. Optional können Sie das Erwärmen oder Abkühlen der Partikel durch ihre Umgebung einbeziehen, oder dafür sorgen, dass die Partikel auf ihrem Weg an Masse gewinnen oder verlieren.

Bei größeren Partikel wird durch eine vollständige Behandlung der Bewegungsgleichungen genau vorhergesagt, wie jedes Partikel im umgebenden Fluid beschleunigt wird. Die Fluidgeschwindigkeit kann manuell eingegeben oder aus einer früheren Analyse übernommen werden. Es stehen auch einige Näherungsmethoden zur Verfügung, die die Simulationszeit erheblich verkürzen, insbesondere für kleine Partikel mit vernachlässigbarer Trägheit.

Drei Räucherstäbchen zu verschiedenen Zeiten, die den erzeugten Rauch als blau-violette Partikeltrajektorien zeigen, wobei die Rauchfahne vom linken zum rechten Stäbchen wächst.

Mathematische Teilchenverfolgung

Als Alternative zu den integrierten Funktionen zum Verfolgen geladener Partikel und Partikel in Strömungen enthält das Particle Tracing Module ein allgemeines Interface zur Lösung jeder beliebigen, von Ihnen spezifizierten Partikelbewegungsgleichung (Mathematical Particle Tracing). Sie können eine beliebige Anzahl benutzerdefinierter Freisetzungsmerkmale, Randbedingungen, Gebietsbedingungen und Kräfte einbeziehen.

Zur Angabe der auf die Teilchen wirkenden Kräfte kann das zweite Newton'sche Bewegungsgesetz oder indirekt eine Lagrange- oder eine Hamilton-Gleichung für das Teilchensystem angegeben werden.

Was Sie mit dem Particle Tracing Module modellieren können

Simulieren Sie das Verhalten von Partikeln in einer Vielzahl von Anwendungen.

Nahaufnahme eines Massenspektrometermodells mit vier Elektroden.

Massenspektrometrie

Ionen durch eine Überlagerung von Gleich- und Wechselfeldern verfolgen.

Nahaufnahme eines Mikrokanalmodells mit sich trennenden Partikeln.

Separation und Filtration

Partikel mit ungleichmäßiger Größenverteilung freisetzen und trennen.

Nahaufnahme einer CVD-Kammer mit injizierten Partikeln.

Tröpfchen und Sprays

Ausbreiten und Verdunsten kleiner Tröpfchen in der Umgebungsluft modellieren.

Nahaufnahme eines Mikromischermodells mit sich mischenden Partikeln.

Mikromischer

Mischen verschiedener Partikelarten visualisieren.

Nahaufnahme eines akustischen Levitatormodells, das die suspendierten Partikel zeigt.

Akoustophorese

Kopplung an ein akustisches Druckfeld, das im Frequenzbereich gelöst wird.

A close-up view of a multipactor model showing the electron trajectories.

Sekundäremission

Exponentielles Elektronenwachstum aufgrund von energetischen Stößen der Teilchen mit der Wand modellieren.

Eine Nahaufnahme eines kreisförmigen Modells, das die Partikel und die Konzentration zeigt.

Diffusiver und advektiver Transport

Kombinieren Sie deterministische und zufällige Kräfte auf Teilchen.

Nahaufnahme eines Rohrbogenmodells, das die Geschwindigkeit der Partikel zeigt.

Erosion

Erosive Verschleißraten durch Auftreffen der Partikel auf Ränder darstellen.

Merkmale und Funktionen des Particle Tracing Module

Das Particle Tracing Module bietet spezielle Werkzeuge zum Verfolgen von Partikeln in Fluiden und Ionen oder Elektronen in externen Feldern.

Eine Nahaufnahme der Einstellungen für die Partikeleigenschaften und ein Mikrosondenplot im Grafikfenster.

Verschiedene Freisetzungsmerkmale

Eine Partikelfreisetzungsfunktion ermöglicht es, anfängliche Partikelpositionen und -geschwindigkeiten zuzuweisen. Sie können festlegen, dass die Partikel von ausgewählten Gebieten, Rändern, Kanten oder Punkten in der Geometrie freigesetzt werden sollen. Für eine feinere Kontrolle über die Anfangspositionen können Sie auch ein Koordinatenfeld eingeben oder die Anfangspositionen und -geschwindigkeiten aus einer Textdatei laden. Spezielle Freisetzungsfunktionen können verwendet werden, um nichtlaminare Ionen- und Elektronenstrahlen mit einer bestimmten Emittanz zu erzeugen, die thermionische Emission von Elektronen aus einer heißen Kathode zu modellieren, oder einen Sprühnebel von Flüssigkeitströpfchen aus einer Düse freizusetzen.

Eine Nahaufnahme der Einstellungen für den nicht-resonanten Ladungsaustausch und ein Modell einer Ladungsaustauschzelle im Grafikfenster.

Monte-Carlo-Stöße-Modellierung

Während sich Ionen und Elektronen ausbreiten, können sie zufällig mit den Gasmolekülen in ihrer Umgebung zusammenstoßen. Sie können Monte-Carlo-Kollisionsmodelle einrichten, in denen jedes Teilchen eine Wahrscheinlichkeit hat, mit Molekülen im umgebenden Gas zu stoßen, basierend auf Daten zu Geschwindigkeit, Gasdichte und Stoßquerschnitt. Bei den Stößen kann es sich um elastische Stöße handeln, aber auch um Ionisierungs- oder Ladungsaustauschreaktionen, bei denen neue Teilchenspezies, wie z. B. Sekundärelektronen, in das Modell eingeführt werden.

Eine Nahaufnahme des Model Builders mit dem hervorgehobenen Knoten Electric Particle Field Interaction und einem Elektronenstrahlmodell im Grafikfenster.

Gekoppelte Teilchen-Feld-Wechselwirkungen

Geladene Teilchen ziehen sich an oder stoßen sich ab, je nachdem, ob ihre Ladungen entgegengesetzte oder gleiche Vorzeichen haben. Dies ist der Grund, warum ein Elektronenstrahl dazu neigt, sich auseinander zu bewegen, wenn er sich vorwärts ausbreitet.

Sie können die Abstoßung oder Anziehung zwischen Teilchen auf zwei verschiedene Arten modellieren. Für eine kleine Anzahl geladener Teilchen können Sie die Coulomb-Kraft direkt definieren. Für eine größere Anzahl von Teilchen können Sie die volumetrische Raumladungsdichte berechnen und sie dann verwenden, um das elektrische Potenzial in der Umgebung der Teilchen zu stören. Der Wechsel zwischen der Berechnung der Elektronenbahnen und des sich daraus ergebenden elektrischen Potenzials ist ein Beispiel für die selbstkonsistente, bidirektional gekoppelte Modellierung der Teilchen-Feld-Wechselwirkung.

Eine Nahaufnahme des Modellbaums mit dem hervorgehobenen Knoten Particle Tracing for Fluid Flow und einem Rohrkrümmungsmodell im Grafikfenster.

Partikel in laminaren und turbulenten Strömungen verfolgen

Um beim Modellieren turbulenter Strömungen Rechenressourcen zu sparen, besteht eine gängige Simulationstechnik darin, die Reynolds-gemittelten Navier-Stokes-Gleichungen (RANS) zu lösen, welche das gemittelte Verhalten der turbulenten Geschwindigkeitsfluktuationen vorhersagen, indem zusätzliche Transportvariablen gelöst werden, anstatt die genaue Geschwindigkeit an jeder Position und zu jedem Zeitpunkt zu berechnen.

Beim Verfolgen von Partikeln in einem turbulenten Fluid mit RANS können Sie die Widerstandskraft modellieren, indem Sie sie als eine Kombination aus zwei Termen behandeln: einen Beitrag aus der mittleren Strömung und einen Beitrag aus den Geschwindigkeitsfluktuationen oder Wirbeln. Sie können diese Wirbel nach dem Zufallsprinzip aus einer Verteilung auswählen, die auf der durchschnittlichen turbulenten kinetischen Energie basiert, indem Sie diskrete und kontinuierliche Random-Walk Modelle verwenden.

Eine Nahaufnahme der Einstellungen für die mathematische Partikelverfolgung und ein Modell einer idealen Tarnvorrichtung im Grafikfenster.

Formulieren und Lösen eigener Bewegungsgleichungen

Sie können benutzerdefinierte Kräfte in einer Newtonschen Formulierung der Bewegungsgleichungen der Partikel aufstellen, die Partikelgeschwindigkeit direkt in einer masselosen Formulierung angeben, oder eine benutzerdefinierte Lagrange- oder Hamilton-Gleichung eingeben.

Zur Lösung der zeitabhängigen Gleichungen der Partikelbewegung bietet die Software COMSOL® eine Reihe verschiedener Löser, darunter robuste implizite Löser, die auch sehr steife Bewegungsgleichungen lösen können, sowie schnelle, genaue Runge-Kutta-Methoden. Ein standardmäßiger Zeitschrittalgorithmus wird auf der Grundlage der funktionalen Form der Partikelbewegungsgleichungen zugewiesen, wobei die Wahl des Lösers ist völlig transparent ist und kann vom Anwender leicht geändert werden kann.

Eine Nahaufnahme der Wandeinstellungen und Modell eines HF-Kopplers im Grafikfenster.

Anpassbare Partikel-Wand-Interaktionen

Während sich die Partikel durch den Simulationsbereich bewegen, erkennen sie automatisch alle Stöße mit Oberflächen in der umgebenden Geometrie. Wenn ein Partikel auf eine Wand trifft, können Sie sein Verhalten steuern: Partikel können aufhören sich zu bewegen, verschwinden, diffus oder spiegelnd reflektieren oder sich in eine benutzerdefinierte Richtung wegbewegen. Sie können auch mehrere Arten der Wandinteraktion an derselben Oberfläche zuweisen und für jede von ihnen eine Wahrscheinlichkeit angeben – oder eine andere Bedingung, die erfüllt sein muss, damit eine bestimmte Art der Wandinteraktion angewendet wird. Alternativ können Partikelstöße mit den Wänden auch eine Sekundärpartikelemission auslösen und somit neue Modellpartikel in die Geometrie einbringen.

Eine Nahaufnahme der Einstellungen für die Partikeleigenschaften und ein Modell einer dielektrophoretischen Trennung im Grafikfenster.

Definieren Sie mehrere Spezies mit unterschiedlichen Eigenschaften

Beim Verfolgen von Partikeln in einem Fluid müssen die Partikeldichte und -größe angegeben werden, um die Widerstands- und Schwerkraftkräfte korrekt anwenden zu können. Je nachdem, welche anderen Kräfte im Modell berücksichtigt werden, kann es erforderlich sein, zusätzliche Informationen wie die relative Dielektrizitätskonstante, die Wärmeleitfähigkeit oder sogar die dynamische Viskosität (bei der Modellierung von Flüssigkeitströpfchen) einzugeben. Sie können die Materialeigenschaften der Partikel entweder direkt eingeben, oder sie aus einer umfangreichen integrierten Bibliothek von Materialeigenschaften laden.

Es ist einfach, verschiedene Arten von Partikeln in derselben Geometrie simultan zu modellieren. Sie können mehrere Arten im selben Modell definieren, jede mit ihren eigenen Materialeigenschaften. Wenn die Partikel aus demselben Material bestehen, aber unterschiedlich groß sind, können Sie alternativ die Masse oder den Durchmesser der freigesetzten Partikel aus einer Verteilung entnehmen.

Eine Nahaufnahme des Model Builders mit dem hervorgehobenen Knoten Space Charge Limited Emission und einem Pierce-Elektronenkanonenmodell im Grafikfenster.

Selbstkonsistente Modellierung raumladungsbegrenzter Emissionen

Das Design moderner Elektronenkanonen erfordert eine genaue Beschreibung der Teilchengeschwindigkeit und des elektrischen Feldes in der Nähe der Kathode oder der Plasmaquelle, wo die Teilchen zunächst mit relativ geringer kinetischer Energie freigesetzt werden. Sie können integrierte Funktionen nutzen, um die raumladungsbegrenzte Emission von Elektronen aus einer Kathode zu modellieren, oder die thermionische Emission mit höherer Genauigkeit behandeln, wenn die thermische Verteilung der freigesetzten Elektronengeschwindigkeiten einen wesentlichen Einfluss auf die Lösung hat.

Eine Nahaufnahme der Einstellungen für die bidirektional gekoppelte Teilchenverfolgung und ein Elektronenstrahlmodell im Grafikfenster.

Relativistische Teilchenverfolgung

Wenn sich die Teilchengeschwindigkeit der Lichtgeschwindigkeit nähert, erfordert die klassische Newtonsche Mechanik einige Änderungen, um die Teilchenbewegung genau zu beschreiben. Das Particle Tracing Module bietet die Möglichkeit, die spezielle Relativitätstheorie bei der Verfolgung sehr schneller Teilchen zu berücksichtigen. Ein Strahl relativistischer Teilchen kann beträchtliche elektrische und magnetische Felder um sich herum erzeugen, so dass ein vollständig selbstkonsistentes Modell sowohl elektrische als auch magnetische Teilchen-Feld-Wechselwirkungen umfasst.

Eine Nahaufnahme des Model Builders mit dem hervorgehobenen Knoten Poincaré Maps und dem Modell einer magnetischen Linse im Grafikfenster.

Partikeltrajektorien visualisieren und animieren

Sie können die momentanen Partikelpositionen als Punkte, Pfeile oder Kometenschweife visualisieren und ihre Bahnen als Linien, Röhren oder flache Bänder darstellen. Sie können die Bahnen mit einem beliebigen Ausdruck einfärben, der auf den Partikeln oder im Raum, den sie einnehmen, definiert ist. Zu den zusätzlichen Postprozessing-Werkzeugen gehören Poincaré-Abbildungen, die den Schnittpunkt der Partikelbahnen mit einer Ebene anzeigen, und Phasenporträts, die die Entwicklung der Partikel im Impulsraum visualisieren.

Sie können problemlos verschiedene Arten von Plots in derselben Plotgruppe kombinieren und dann die Partikelbewegung animieren. Plots und Animationen können in eine Datei exportiert werden, oder Sie können die Rohdaten der Lösung zur weiteren Analyse exportieren. Eingebaute Operatoren und Variablen bieten einen praktischen Überblick über die Partikelstatistiken.

Jedes Unternehmen und jeder Simulationsbedarf ist einzigartig.

Um zu beurteilen, ob die COMSOL Multiphysics® Software Ihren Anforderungen entspricht, kontaktieren Sie uns bitte. Wenn Sie mit einem unserer Vertriebsmitarbeiter sprechen, erhalten Sie persönliche Empfehlungen und vollständig dokumentierte Beispiele, die Ihnen helfen, das Beste aus Ihrer Evaluierung herauszuholen und die beste Lizenzoption für Ihre Bedürfnisse zu wählen.

Klicken Sie einfach auf die Schaltfläche "COMSOL kontaktieren", geben Sie Ihre Kontaktdaten und Ihre spezifischen Kommentare oder Fragen ein und senden Sie Ihre Anfrage ab. Sie erhalten innerhalb eines Werktages eine Antwort von einem Vertriebsmitarbeiter.

Nächster Schritt

Fordern Sie eine Software-Demo an

COMSOL kontaktieren