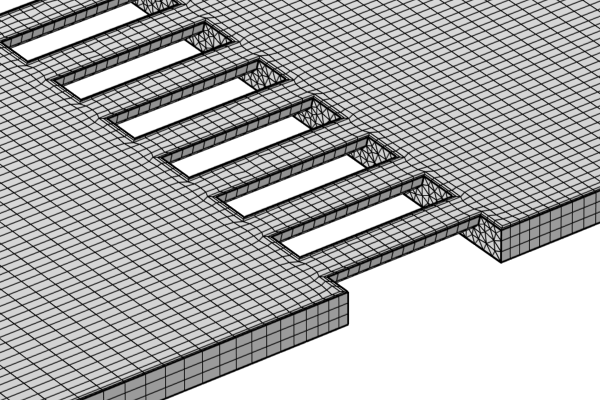
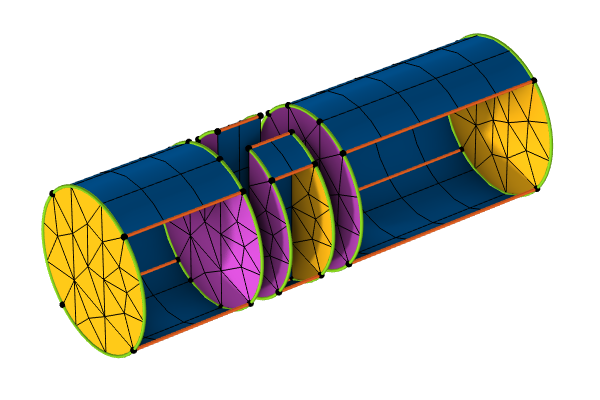
Fundamentals of Swept Meshing
The COMSOL Multiphysics® software contains many features and functionality that enable you to generate different types of meshes. Depending on the application, certain mesh types will be better suited and provide advantages for discretizing your model geometry, such as requiring significantly less memory when solving the model. One of these mesh types is a swept mesh. So, what exactly is a swept mesh and when should you consider using one in your model? In this article, we will address questions such as these and more.
What is Swept Meshing?
For now, let us consider a simplified definition of swept meshing in order to get a quick grasp of this operation. Swept meshing is a process that can only be applied when working with 3D geometries, and it involves extruding a surface mesh throughout the domain. It is only possible to build a swept mesh if the geometry domains meet certain criteria. This is addressed in Part 2 of this course on swept meshing, along with a third part focusing on rules and procedures for how to build swept meshes.
This 3D geometry of a single conductor coil is swept meshed by sweeping the cross section. Since the surface mesh was meshed with triangles, the resulting volume mesh is composed of prisms.
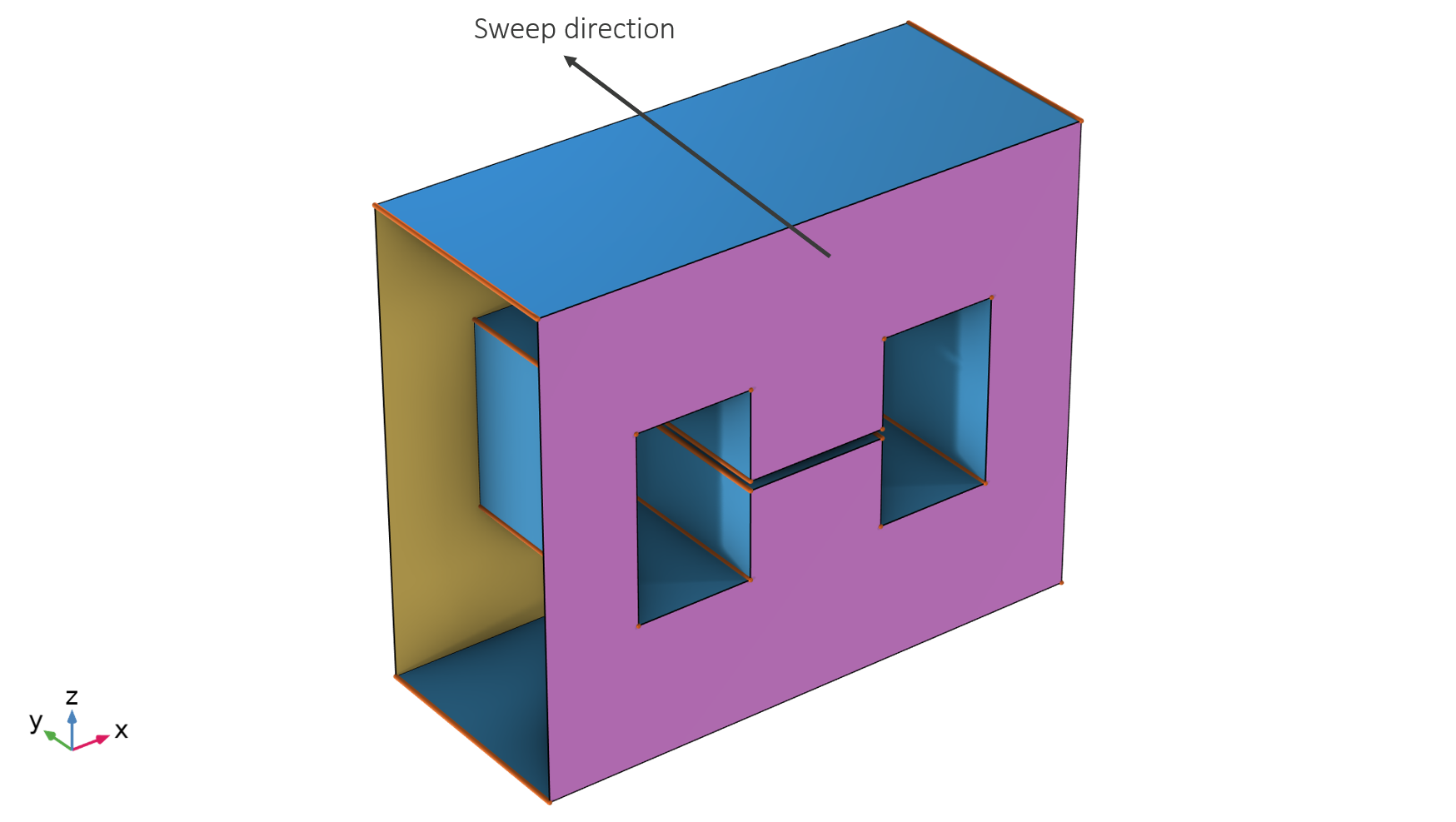
By construction, a swept mesh is a type of structured or semistructured mesh composed of prisms or hexahedra. By structured, we mean a mesh where the interior mesh vertices are adjacent to the same number of elements. A mesh is structured in the sweep direction and then either structured or unstructured orthogonally to the sweep direction.
An outline of the process of swept meshing: A magnetic core with an air gap.
Now that we have reviewed the concept of what a swept mesh is, let us explore examples of and use cases for swept meshing.
Advantages and Examples of Swept Meshes
The purpose of the swept mesh is to represent the geometry and solution of the computed fields with accuracy, while using minimal computational resources. In some cases, the default tetrahedral mesh generated is either not good enough to capture the gradients in the solution, for example, or is too computationally expensive to allow the model to be solved on standard machines in an acceptable amount of time. When gradients are localized, both of these can be true. Swept meshes offer a solution for this, and are applicable and relevant for any physics application area.
 Eight tutorial models that use swept mesh; the examples shown include electromagnetism, MEMS, batteries, semiconductors, CFD, structural mechanics, acoustics, and extended and infinite domains.
Tutorial models examples (for different application areas) that use a swept mesh. You can find each of these tutorial models in the application libraries.
Eight tutorial models that use swept mesh; the examples shown include electromagnetism, MEMS, batteries, semiconductors, CFD, structural mechanics, acoustics, and extended and infinite domains.
Tutorial models examples (for different application areas) that use a swept mesh. You can find each of these tutorial models in the application libraries.
While swept meshes might give the impression that they are the universal solution to all or most models, there are still some cases where a tetrahedral mesh is recommended instead. For instance, a tetrahedral mesh would be better in cases that involve:
- Complex topology
- A mesh that needs to grow in size at different rates depending on the location and direction
Note that these cases may only occur in some portion of the geometry, while the rest can be swept meshed. In that case, different mesh types can be combined in order to implement the best elements of each.
For a swept mesh, there are three major advantages, regardless of the physics you are solving. For instance:
- Using it results in a lower number of mesh elements.
- Prisms and hexahedra are typically more robust for thin geometries.
- It is efficient to generate.
For additional information on the advantages of swept meshing, see Supplement A.
Use Cases
We have presented the three major advantages of swept meshes, which are not physics specific. We will now present concrete examples where those advantages are put to use:
- Slender Structures with High Aspect Ratios
- Solution has a Specific Directionality
- Thin or Narrow Regions Inside Domains
- Resolution of High Gradient in Solution
- Extending the Computational Domain for Better Placement of Boundary Conditions
- Deforming Domains
- Infinite Element Domains and Perfectly Matched Layers
- More Generic Geometries
We expand on each of these specific use cases below.
Slender Structures With High Aspect Ratio
When modeling, you may encounter situations where the geometry in one dimension is significantly larger or smaller than the other two dimensions. This is often the case for integrated circuits and printed circuit boards, which are important in the MEMS industry, or when modeling cables and pipes, whether it be for modeling CFD, solid mechanics, or electromagnetism.
For a geometry that is slender or contains slender regions, a tetrahedral mesh may be good for modeling some physics phenomena, but not all. Because of this, it can be crucial to be able to generate a swept mesh where the elements are stretched in some direction and still have a good-enough quality.
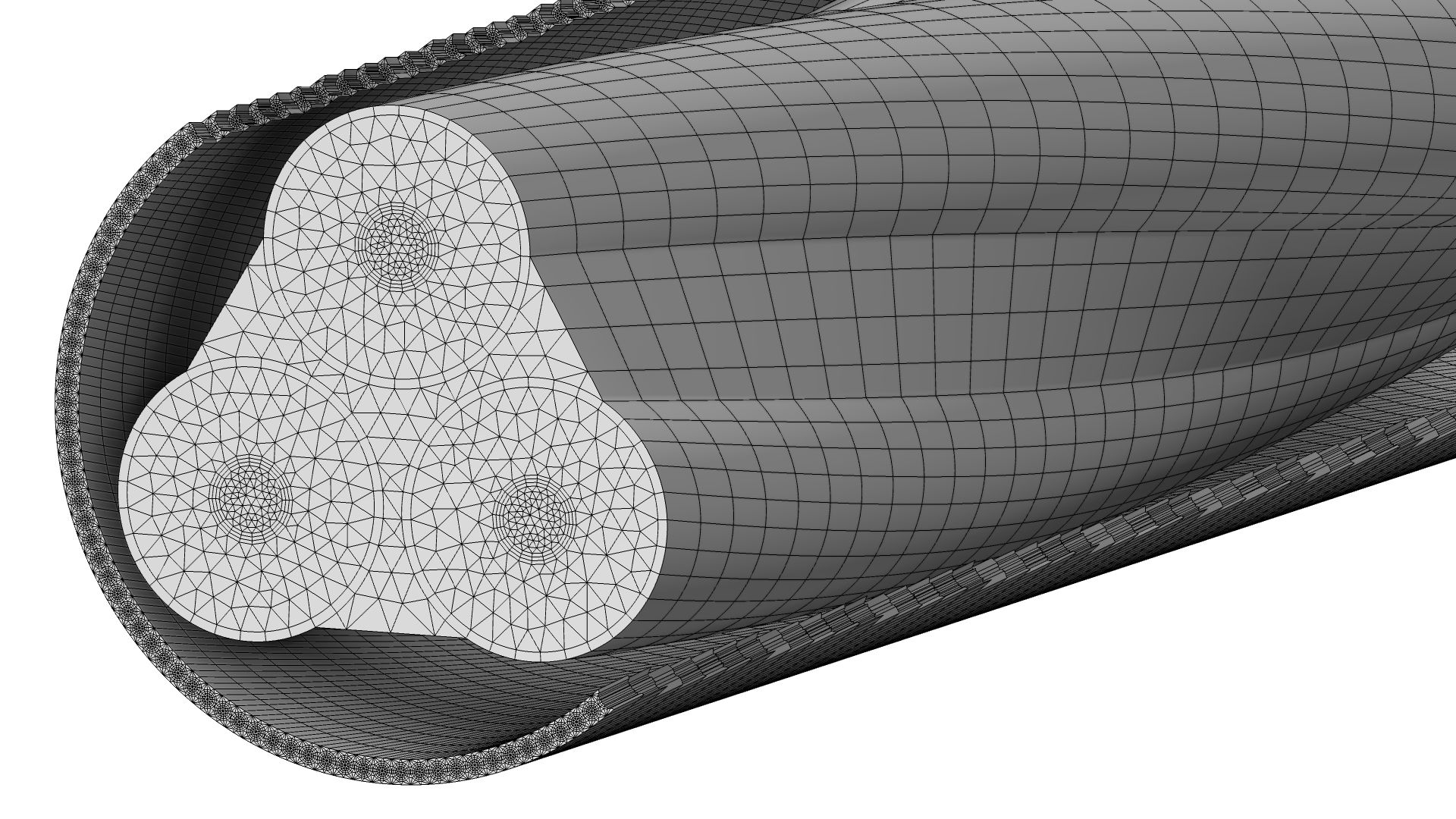
The mesh in the Submarine Cable 7 — Geometry & Mesh 3D tutorial model. The challenge is to find a mesh that resolves the cable geometry and the physics as best as possible, while still keeping the DOF count low enough to have a reasonable solving time.
Solution has a Specific Directionality
For CFD problems, the gradient in the solution is mostly in the direction normal to the flow. Given that the walls do not have a slip condition, a region of high-velocity gradient is forming next to the wall due to viscous effects — this is the so-called boundary layer. This means that the cross section of the swept mesh needs to be well resolved, especially near the walls. In the direction of the flow, the elements can be much coarser, as it is enough to resolve the slow gradient. The boundary layer is resolved by adding a boundary layer mesh along the wall boundaries, while the slow gradient allows for stretched elements in the direction of the flow.
 A model of a pipe elbow showing the mesh and velocity gradient.
In the Flow Through a Pipe Elbow tutorial model, the cross section needs to be meshed with a finer mesh size, especially near the walls to resolve the gradient of the solution. The mesh discretization along the flow gradually increases in size as the the gradient of the velocity in this direction becomes smaller. (Each cross section exhibits approximatively the same velocity profile.)
A model of a pipe elbow showing the mesh and velocity gradient.
In the Flow Through a Pipe Elbow tutorial model, the cross section needs to be meshed with a finer mesh size, especially near the walls to resolve the gradient of the solution. The mesh discretization along the flow gradually increases in size as the the gradient of the velocity in this direction becomes smaller. (Each cross section exhibits approximatively the same velocity profile.)
We can use this same strategy to model any physics phenomenon that has a slow gradient in one direction. This typically happens when solving a model with the Electromagnetic Waves, Beam Envelopes interface, which is used when the propagation length is much longer than the wavelength. The mesh does not need to resolve the wave on a wavelength scale, but rather the beating between the two waves. In some cases, only one element is needed along the propagation direction. (For more information, read this blog post.) In the Directional Coupler tutorial model, few mesh elements are needed in the wave propagation direction.
Thin or Narrow Regions Inside Domains
Swept meshes can be useful for small details and narrow regions in geometries. To obtain the best possible mesh in these scenarios, you may need to partition the computational domain in order to sweep a mesh in each part separately and also control the size and type of elements in each partitioned domain. This strategy of meshing domains with different settings can be found in our blog post, Best Practices for Meshing Domains with Different Size Settings. The main takeaway is to start sweeping the mesh from the domain where you want to use the smallest mesh size, which is generally either the smallest domain or the one with the steepest gradients in the solution. A typical example is the presence of small channels connecting wider domains in fluid dynamics applications. We know the solution will have a steep gradient in these regions since it may be the place of an accelerating flow.
The default tetrahedral mesh (left) versus a swept mesh (right) in a CFD application with narrow regions. The boundary layers are added as a last step once the domain mesh has been generated.Resolution of High Gradient in the Solution
In semiconductor models, for example, it is common that the solution gradient has to be well resolved in one direction only. The various physical processes that are involved often require very different length scales. Most of all, doping profiles need to be correctly resolved, as explained in this blog post.

In this bipolar transistor tutorial model, the mesh used is a structured swept mesh where the resolution in the vertical direction is largest around the p-n junctions and near the electrical contacts on the top and bottom surfaces.
The use of swept meshing in semiconductor models is even more crucial, as most models are based on a finite volume method since they inherently conserve current and therefore usually provide the most accurate result for the current density of the charge carriers. For the same mesh, this method requires more DOFs than the finite element method. Given that 3D semiconductor computations can take days to solve, anything to make that process more economical is welcomed and encouraged, of which swept meshing is one. It's use is particularly well suited for these types of problems.
Extending the Computational Domain for Better Placement of Boundary Conditions
Boundary conditions define how the solution connects to the outside world. The interior field will depend on which kind of condition we use, which value we assign to it, and where we place the condition itself. For some models, where to place the boundary conditions is obvious.
We always need to keep in mind that, at the limit of our computational domain, the solution (or its gradient) is imposed. Broadly speaking, when we have convective or propagation terms, we should make sure that the boundary condition is placed far enough so not to influence the solution, as explained in this blog post.
When you need to enlarge the computational domain to place the boundary condition in the appropriate spot, what one usually does is extend the computational domain in a specific direction. Extruded domains are perfect fits for swept meshes considering that you are also expecting the solution field to develop in that specific direction.
Deforming Domains
When deforming a geometry during computations, sliver elements might be generated due to a compression or expansion. As we saw earlier, the element quality of a tetrahedral element is more sensitive to decompression than a prism or hexahedron. If a tetrahedral mesh is used when simulating deformations, it might lead to:
- A need to remesh the deformed configuration one or several times when the elements become too distorted. This results in increased computation time, as the remeshing process takes time and the solution needs to be reinitialized in the new mesh.
- A dense mesh near narrow domain regions, increasing the simulation time by increasing the number of DOFs.
- A risk that the simulation cannot converge due to bad-quality elements.
In the case where you solve for a translation, the direction of compression or expansion can be predicted in advance. This would be the perfect opportunity to use a swept mesh to reduce the need of remeshing. If the geometry is partitioned to allow for a sliding mesh (as described in this blog post), the problem will be more constrained, making the computation even faster and more robust.
In this power switch tutorial model, iron plungers are moved by means of the magnetic attraction exerted by current flowing in the coils surrounding it. In the animation, the magnetic flux density norm is colored in the plunger domains. The air gap (white mesh) between the plunger and the coil is separated from the rest of the air domain (gray mesh) in order to be swept meshed. As the plunger moves toward the lower E-core, it closes the air gap, compressing the swept mesh vertically.
Infinite Element Domains and Perfectly Matched Layers
Some models need a region of infinite extent. They can be modeled as either infinite element domains, perfectly matched layers (PML), or absorbing layers. For PMLs and absorbing layers, it is important that the mesh matches the coordinate stretching direction, that is, the direction of absorption. The reason for this is that these virtual domains are numerically stretched out toward infinity, so we must take into account that the mesh elements will be virtually elongated.
If an infinite element domain or PML is used by the physics, a swept mesh will automatically be generated by the physics-controlled mesh.
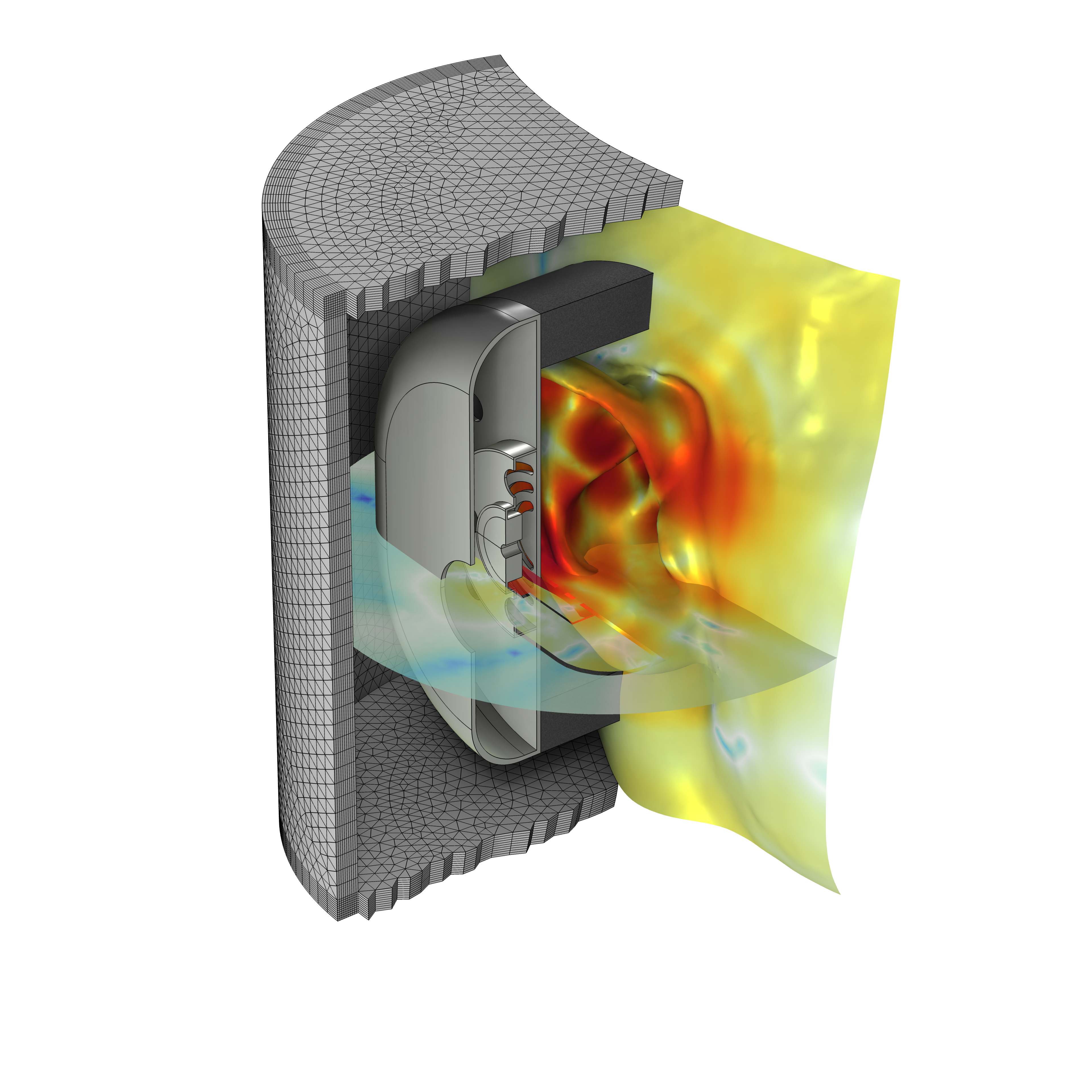
In the Headphone on an Artificial Ear tutorial model, cylindrical PMLs are used around the geometry, which are meshed with a swept mesh (represented partially in the image in order to visualize the interior geometry). The resulting sound pressure level at 20 kHz is depicted on the manikin and slice of the air domain.
More Generic Geometries
What about domains of a more generic shape? For those, a swept mesh can still be used. Recall the first advantage of swept meshes: the swept mesh will require about half as much of DOFs compared to a tetrahedral mesh. However, domains of more general shape may require some additional work to be made sweepable. We will look further into this later in the course.
It is not always possible to use a swept mesh for the whole geometry. Nonetheless, you can get the best of both worlds by combining a swept and a tetrahedral mesh by generating a swept mesh in as much of the geometry as possible, and then meshing the rest with a tetrahedral mesh.
 The Centrifugal Pump model with various mesh elements.
A tetrahedral mesh is combined with a swept mesh in the Centrifugal Pump tutorial model.
The Centrifugal Pump model with various mesh elements.
A tetrahedral mesh is combined with a swept mesh in the Centrifugal Pump tutorial model.
Alternatives to Generating Meshes for Thin Domains
We have discussed at great length the opportunities for using swept meshes to discretize the model geometry, however, there are some times in which an alternative strategy might be optimal. This is especially in cases that involve working with thin and/or slender geometries. COMSOL Multiphysics® has many specialized physics interfaces as well as physics feature nodes that enable you to more efficiently model thin regions with high aspect ratios. There are also options for modeling such regions as surfaces or edges instead of as 3D domains. You can learn about this functionality and the corresponding features in COMSOL Multiphysics® in the following blog posts:
- Coupling Structural Mechanics Interfaces
- Analyze Thin Structures Using Up and Down Operators
- Modeling Piezoelectricity: Which Module to Use?
The physics interfaces and boundary conditions mentioned in these blog posts enable you to easily address thin domains or layers in geometry. In addition, you can see what features are available for CFD simulations by referencing the fluid flow specification chart.
Further Learning
In this article, we focused on understanding what swept meshes are and when you should use them, as well as when to use them in combination with a tetrahedral mesh. Several examples were showcased in this article, and we encourage you to use the provided links to explore the models further. Additionally, in the software under the Application Libraries you can search @tag:swe to find any tutorial model examples that use swept meshing for the model geometry. By navigating to the appropriate application area you are interested in, you can find relevant examples and understand the logic behind why a swept mesh was used or was incorporated into a mesh as well as how it was implemented.
Submit feedback about this page or contact support here.