
In diesem Blog-Beitrag untersuchen wir eine 12-nutige, 10-polige Permanentmagnetmaschine, die mit der Software COMSOL Multiphysics® und dem AC/DC Module modelliert wurde. Diese Maschine dient als repräsentatives Beispiel für ein rotierendes Gerät und hat einen Außendurchmesser von 35 mm und eine axiale Länge von 80 mm. Mit geringfügigen Änderungen an den Eingaben kann dasselbe Modell zu einem Motor oder einem Generator gemacht werden.
Dies ist der erste Blog-Beitrag einer zweiteiligen Reihe, in der es darum geht, wie man mithilfe der Modellierungs- und Nachbearbeitungsfunktionen der Software COMSOL Multiphysics® mehr über einige Designaspekte rotierender Maschinen erfahren kann. Teil 2 befasst sich mit der Berechnung von Verlust, Temperatur und Wirkungsgrad in Elektromotoren.
Elektromotor- und Generatordesigns: Modelleinrichtung
In einem Permanentmagnetmotor rotieren die Magnetfelder des Rotors synchron mit den Magnetfeldern, die durch die Statorströme erzeugt werden. Durch die Interaktion der Magnetfelder von Rotor und Stator wird das Nettodrehmoment erzeugt, das dem Motor die Umwandlung der Wicklungsströme in mechanische Energie ermöglicht. Aufgrund der synchronen Erregung wird das unmittelbare Drehmoment in einem Permanentmagnetmotor stark von der Rotorwinkelposition beeinflusst, da die Position mit den Statorströmen synchronisiert ist. Dies ist bei Asynchronmaschinen anders, bei denen die Statorwicklungen die Rotormagnetfelder als Funktion der Geschwindigkeitsverzögerung zwischen Rotor und Stator induzieren (daher der gängige Name Induktionsmaschine).
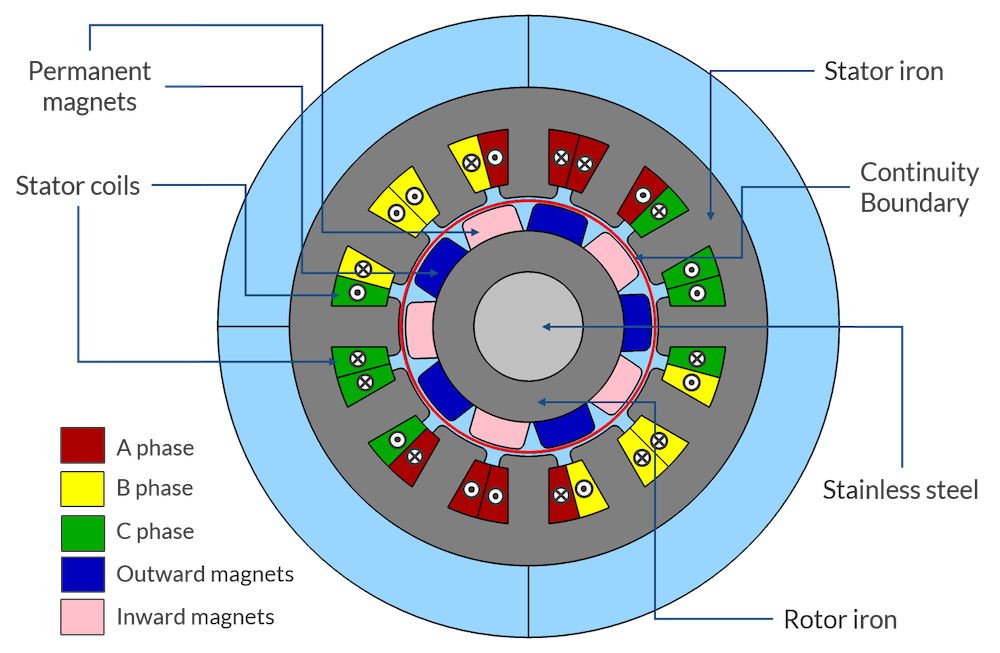
Schema des Permanentmagnetmaschinenmodells.
Die Spulenerregung hat die Form: I = I_m cos(\kappa \alpha + \phi), wobei I_m der Spitzenstrom, \kappa ein Skalierungsfaktor, der von der Anzahl der Pole abhängt, \alpha der Rotorwinkel und \phi der Phasenwinkel ist. In diesem Beispiel wird die Anregung für die drei Phasen jeweils angegeben durch: I_a = I_m cos(\kappa \alpha), I_b = I_m cos(\kappa \alpha – {120}^{\circ}) und I_c = I_m cos(\kappa \alpha – {240}^{\circ}).
Um sicherzustellen, dass die Anziehungs- und Abstoßungskräfte zwischen den Stator- und Rotorpolen ein unidirektionales Drehmoment erzeugen, muss der Skalierungsfaktor \kappa so gewählt werden, dass die Felder der Statorspulen ihre Richtung umkehren, wenn sich der Rotor um einen Winkelbereich eines Rotormagneten bewegt (die Magnete haben eine wechselnde Polarität). Sein Wert wird angegeben durch \kappa = \frac{{180}^{\circ}}{{360}^{\circ}/N_p}, wobei N_p die Anzahl der Rotorpole ist. Der Nenner gibt die Winkelspanne eines einzelnen Rotorpols an.
Untersuchung und Optimierung der Magnetfeldverteilung
Die Magnetfeldverteilung ist ein sehr wichtiger Designfaktor bei elektrischen Maschinen. Bei synchron rotierenden Maschinen ist die räumliche Verteilung des Luftspaltflusses (der zwischen Rotor und Stator ausgetauschte Fluss) ein Schlüsselparameter für die Untersuchung induzierter Spannungen. Die Statorphasenspannung ist nur dann sinusförmig, wenn der radiale Magnetfluss eine sinusförmige Verteilung entlang der Rotorperipherie aufweist. Diese räumliche Wellenform wird auch als Luftspalt-Durchflutungswelle (Magnetomotive Force Wave) bezeichnet. Wenn die Durchflutungswelle nicht sinusförmig ist, werden in die induzierte Spannung Oberschwingungen höherer Ordnung eingeführt.
In diesem Modell bewerten wir die radiale Komponente der magnetischen Flussdichte entlang des Kontinuitätsrands, um die Luftspalt-Durchflutungswelle zu erhalten. Während sich der Rotor dreht, können wir die Entwicklung der Durchflutungswelle im Laufe der Zeit beobachten. Allein durch Betrachtung ist zu erkennen, dass die induzierte Spannung nicht perfekt sinusförmig sein wird. In der kommenden Blog-Reihe werden wir erklären, wie die räumliche und zeitliche Fourier-Transformation des magnetischen Flusses im Luftspalt ermittelt werden kann und wie diese mit dem verketteten Fluss und der harmonischen Verzerrung der Spannung in Zusammenhang stehen.
Links: Änderung der magnetischen Flussdichte bei Rotordrehung. Rechts: Verlauf der Luftspalt-Durchflutungswelle bei Rotordrehung.
Untersuchung und Optimierung des mechanischen Drehmoments
Die Statorwicklungen für eine bestimmte Nut-/Polkombination eines Permanentmagnetmotors können mit verschiedenen Methoden angeregt werden. Das im Schaltplan des Permanentmagnetmaschinenmodells (erste Abbildung im Blog-Beitrag) gezeigte Muster ist eine Möglichkeit, einen 12-nutigen, 10-poligen Permanentmagnetmotor anzutreiben. Die Statorwicklungserregung (oder die anfängliche Rotorposition) muss so eingestellt werden, dass ein maximales Drehmoment auf den Rotor ausgeübt wird. Zu diesem Zweck wird der Rotor mit einer anfänglichen Winkelverschiebung versehen. Der Rotorwinkel \alpha wird über eine Winkelspanne von einem Rotormagneten variiert und das durchschnittliche Drehmoment berechnet. Der Wert der anfänglichen Winkelverschiebung, der dem maximalen durchschnittlichen Drehmoment entspricht, wird als Anfangsposition des Rotors gewählt. Auf diese Weise lässt sich leichter erkennen, welche relative Position von Stator und Rotor das maximale Drehmoment erzeugt.
Im vorliegenden Fall werden zwei Maxima beobachtet:
- Positives Maximum, das einer elektrischen Maschine entspricht, die im Motorbetrieb arbeitet, also elektrische Leistung in mechanische Leistung umwandelt
- Negatives Maximum, das einer elektrischen Maschine entspricht, die im Generatorbetrieb arbeitet, also mechanische Energie in elektrische Energie umwandelt
Die im nächsten Abschnitt angegebene Wellenform des Rotordrehmoments entspricht dem positiven Maximum der durchschnittlichen Rotordrehmomentkurve.
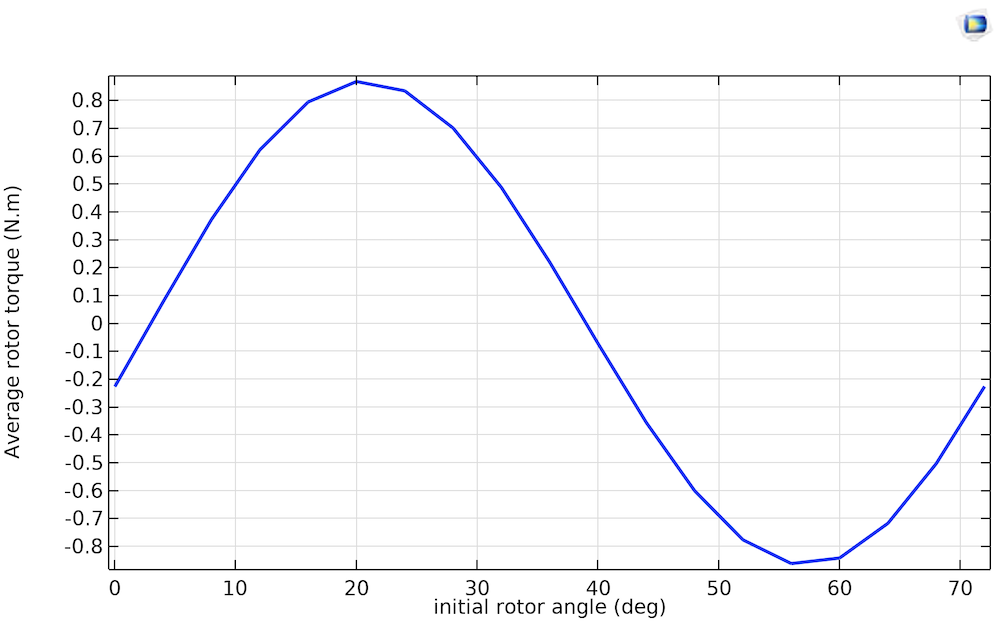
Veränderung des durchschnittlichen Rotordrehmoments in Abhängigkeit vom anfänglichen Rotorwinkel über die Spannweite von zwei Rotorpolen (2 \times \frac{{360}^{\circ}}{N_p} = {72}^{\circ}).
Untersuchung und Optimierung des Eisenverbrauchs und der Eisenverluste
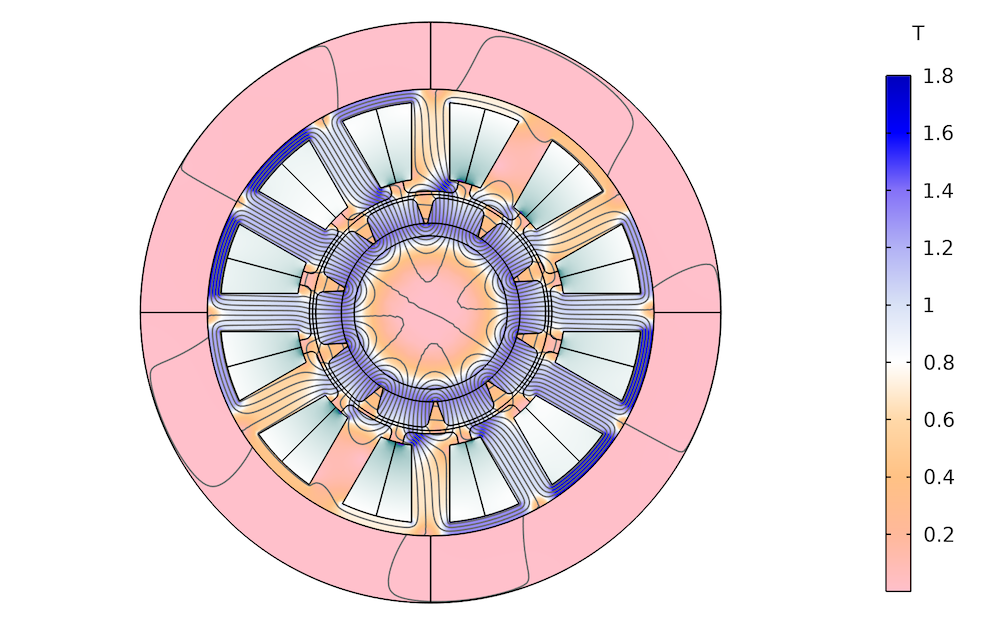
Mit einem Plot der magnetischen Flussdichte können wir die Verteilung der Flussdichte im Eisenkern untersuchen. In einigen Bereichen der Geometrie kann das Joch einen Engpass bilden, der den Wert der magnetischen Flussdichte in den Sättigungsbereich der B-H-Kurve verschieben kann. In anderen Bereichen ist es breit genug, um Gebiete mit geringer Feldstärke zu verursachen. Wenn ein bestimmter Teil des Jochs durchgehend ein schwaches Feld aufweist, wird dieser Teil für die Drehmomentproduktion nicht ausreichend genutzt. Bildet ein Teil einen durchgehenden Engpass, sollte dieser Teil wahrscheinlich verbreitert werden.
In diesem Beispiel wird die Eisenstärke in Rotor und Stator variiert und ihre Auswirkung auf das Rotordrehmoment untersucht. Um ein maximales Drehmoment zu erzeugen, wird der anfängliche Rotorwinkel auf {20}^{\circ} eingestellt, wie aus der durchschnittlichen Drehmomentkurve im vorherigen Abschnitt hervorgeht. Wie Sie den folgenden Plots und der Drehmomentkurve entnehmen können, ist die Eisennutzung optimal, wenn die Eisenstärke etwa 2 mm beträgt: Eine Dicke von weniger als 2 mm wirkt sich negativ auf das Drehmoment aus, während eine größere Dicke unnötiges Material – und damit Gewicht und Kosten – für den Motor zur Folge hat.
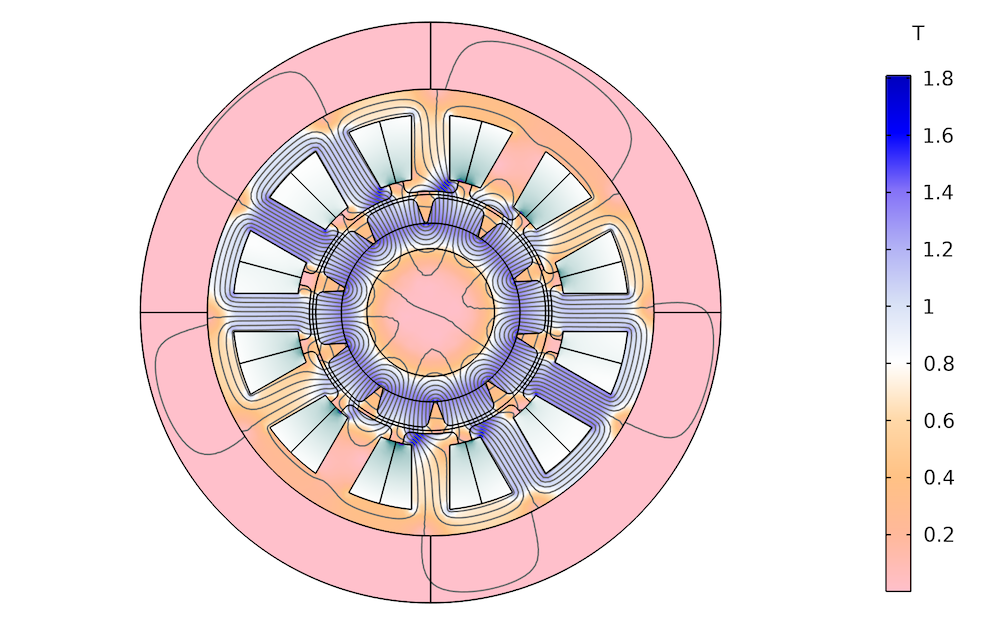
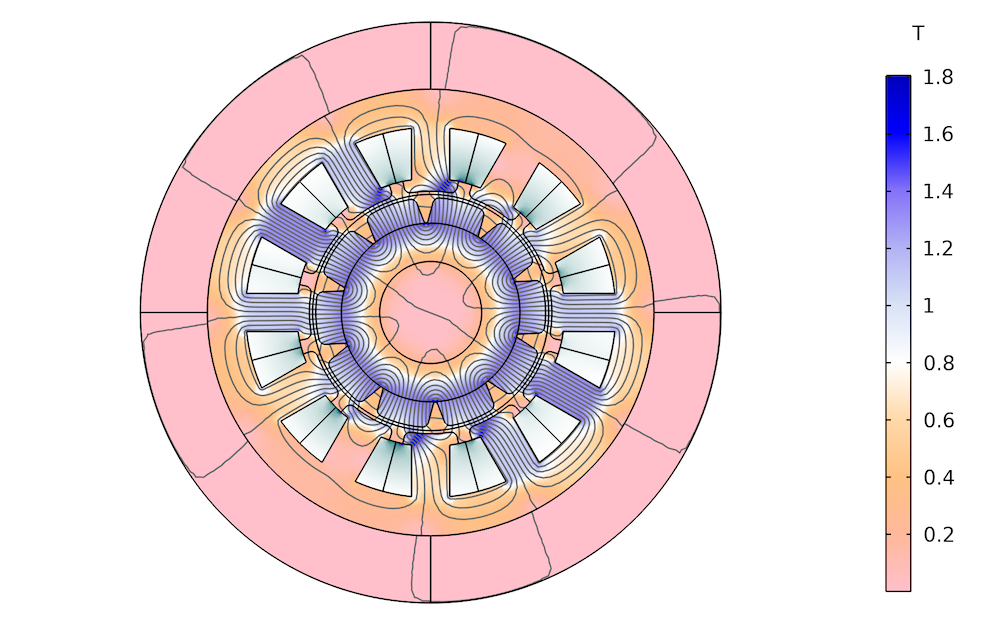
Verteilung der magnetischen Flussdichte bei unterschiedlichen Eisenstärken. Links: 1 mm. Mitte: 2 mm. Rechts: 3 mm.
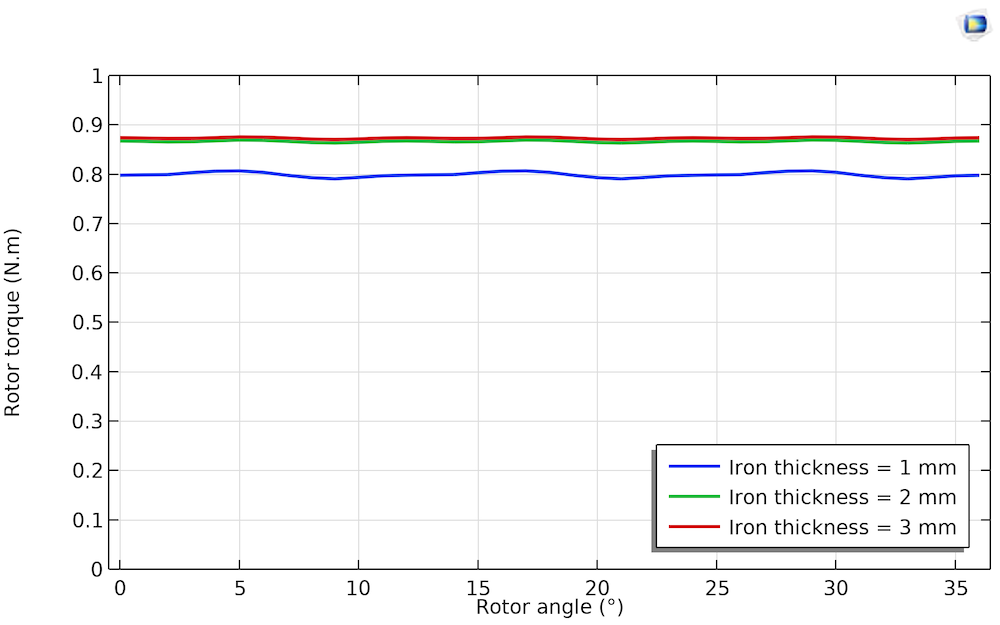
Veränderung der Wellenform des Rotordrehmoments in Abhängigkeit von der Eisenstärke.
Das ist jedoch nicht alles: Bei der Bestimmung der Eisenstärke müssen weitere Faktoren berücksichtigt werden, wie die mechanische Festigkeit und die Widerstands- und Magnetverluste. Bei der Untersuchung der Flussdichte und des Drehmoments kann auch der Einfluss der variierenden Eisenstärke auf die Eisenverluste bewertet werden. Ab der COMSOL Multiphysics Version 5.6 steht ein integriertes Feature Loss Calculation zur Verfügung, um die Kupfer- und Eisenverluste mithilfe der Steinmetz-Gleichung, der Bertotti-Formel oder eines benutzerdefinierten Verlustmodells einfach zu bewerten. In Teil 2 dieser Blog-Reihe werden wir die Variation der Eisen- und Kupferverluste, den daraus resultierenden Temperaturanstieg und die Auswirkungen auf den Wirkungsgrad der Permanentmagnetmaschine untersuchen.
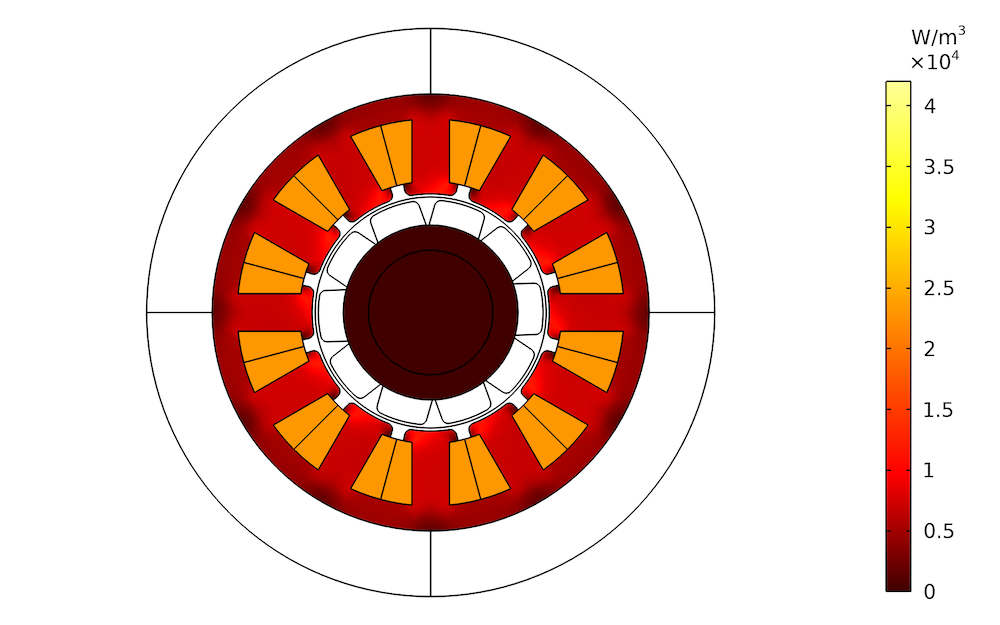
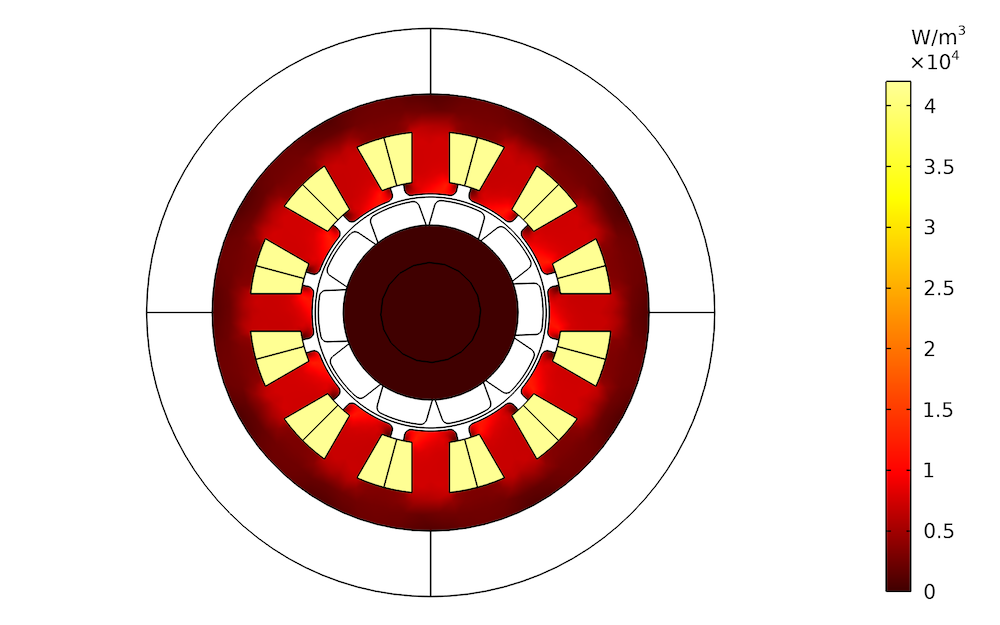
Verteilung der Eisenverluste bei unterschiedlichen Eisenstärken. Links: 1 mm. Mitte: 2 mm. Rechts: 3 mm.
Zusammenfassung
Wir haben die Verwendung einiger Funktionen von COMSOL Multiphysics und des AC/DC Module zur einfachen Untersuchung einiger Designaspekte von rotierenden Maschinen besprochen. Anhand des Liniendiagramms der radialen magnetischen Flussdichte im Luftspalt kann festgestellt werden, ob die induzierte Spannung sinusförmig ist. Mit COMSOL Multiphysics kann ein Parametric Sweep verwendet werden, um den anfänglichen Rotorwinkel zu bestimmen, der das maximale Rotordrehmoment erzeugt. Der Oberflächenplot der magnetischen Flussdichte in der Maschine ermöglicht es Ihnen, visuell zu bestimmen, ob die Eisennutzung für eine effiziente Drehmomentproduktion optimal ist. Die Auswirkung der Eisenstärke auf die Eisenverluste kann ebenfalls beobachtet werden, indem die in COMSOL Multiphysics integrierten Verlustmodelle verwendet werden.
Dieser erste Blog-Beitrag der Reihe veranschaulicht, wie die leistungsstarken Modellierungs- und Nachbearbeitungsfunktionen von COMSOL Multiphysics für wertvolle Einblicke in das Design rotierender Maschinen genutzt werden können. In den folgenden Blog-Beiträgen werden Methoden zur Drehmomentberechnung, Effizienzberechnung, Analyse von Eisenverlusten und thermischer Leistung sowie die Untersuchung von Motorvibrationen und -geräuschen ausführlich behandelt.
Probieren Sie es selbst aus
Modellieren Sie den hier besprochenen Elektromotor, indem Sie auf die folgende Schaltfläche klicken:







Kommentare (0)