
Die Faltenbildung ist relevant für die verschiedensten Forschungsbereiche, die von aufblasbaren Antennen in der Raumfahrt bis hin zu der bekannten Faltenbildung der Haut im Bioengineering reichen. Unabhängig davon, in welchem Gebiet sie arbeiten, sind Ingenieure und Wissenschaftler, die sich mit dünnen Strukturen befassen, mit dem der Faltenbildung zugrunde liegenden Mechanismus vertraut: eine fehlende oder verringerte Steifigkeit, wenn eine dünne Struktur Druckspannungen ausgesetzt ist. In diesem Blog-Beitrag werden wir erläutern, wie die Faltenbildung mit der Software COMSOL Multiphysics® modelliert werden kann.
Einführung
Bei Strukturmechanik-Simulationen werden dünne Strukturen in der Regel entweder mit Schalen- oder Membranelementen modelliert. Schalenelemente berücksichtigen die Biegesteifigkeit der Struktur, während Membranelemente dies nicht tun. Dieser grundlegende Unterschied bestimmt, wie die beiden Elementtypen die Modellierung der Faltenbildung handhaben. Wenn die Biegesteifigkeit berücksichtigt wird, wie bei der Schalenmodellierung, wird die Faltenbildung bei einer kritischen Druckspannung beobachtet, die durch die Biegesteifigkeit gekennzeichnet ist. Wird die Biegesteifigkeit hingegen nicht berücksichtigt, wie bei der Membranmodellierung, wird die Faltenbildung beim Einsetzen der Druckspannungen beobachtet.
In beiden Fällen wird die Faltenbildung als Instabilität betrachtet und ist auch als lokales Knicken bekannt. Bei der Modellierung der Faltenbildung mit Schalenelementen ist eine Post-Buckling-Analyse erforderlich. Dabei ist zu beachten, dass die Diskretisierung des Netzes und etwaige geometrische Mängel die Endergebnisse erheblich beeinflussen können. Der Vorteil der Schalenmodellierung besteht in der Gewinnung detaillierter Informationen über die Eigenschaften der Faltenbildung, wie Wellenlängen und Amplituden. In vielen Modellierungsszenarien sind die detaillierten Eigenschaften der Faltenbildung jedoch nicht so relevant wie die tatsächliche Vermeidung der Faltenbildung im Problembereich. In solchen Fällen kann die Modellierung der Faltenbildung mit Membranelementen von Vorteil sein, da dieser Ansatz rechnerisch kostengünstig ist und eine bessere numerische Stabilität bietet.
Im Folgenden werden wir uns diese beiden Modellierungsansätze nacheinander ansehen. In COMSOL Multiphysics® werden Schalen- und Membranelemente mit den Interfaces Shell bzw. Membrane modelliert.

Ein weiteres bekanntes Beispiel für Faltenbildung: in einem Segel. Foto von Karla Car auf Unsplash. Das Originalwerk wurde geändert.
Modellierung mit dem Interface Membrane
Dünne Strukturen, die mit dem Interface Membrane modelliert werden, befinden sich bei der Verformung in einem von drei möglichen Zuständen:
- Straff — wenn beide Hauptspannungen in der Ebene positiv sind
- Schlaff — wenn beide Hauptspannungen in der Ebene negativ sind
- Faltig — wenn eine der Hauptspannungen in der Ebene negativ ist
In der gewöhnlichen Membrantheorie wird eine Formulierung mit voller Dehnungsenergie verwendet, die Druckspannungen in den faltigen Bereichen berücksichtigt, was wiederum zu instabilen Gleichgewichtslösungen führt. Um die durch Druckspannungen verursachte Instabilität des Gleichgewichts zu vermeiden, wurde die modifizierte Membrantheorie (basierend auf der Spannungsfeldtheorie) entwickelt. Die modifizierte Membrantheorie liefert einen uniaxialen Spannungszustand in der faltigen Region und einen Spannungszustand von Null in der schlaffen Region, wodurch die Instabilität des Gleichgewichts vermieden wird. Die modifizierte Membrantheorie kann in zwei Hauptansätze aufgeteilt werden: Modifikationen des Verformungstensors und Modifikation der konstitutiven Beziehung.
Modifizierte Formulierung des Verformungstensors
Um die Kinematik der Faltenbildung zu verstehen, betrachten Sie die folgende Abbildung:
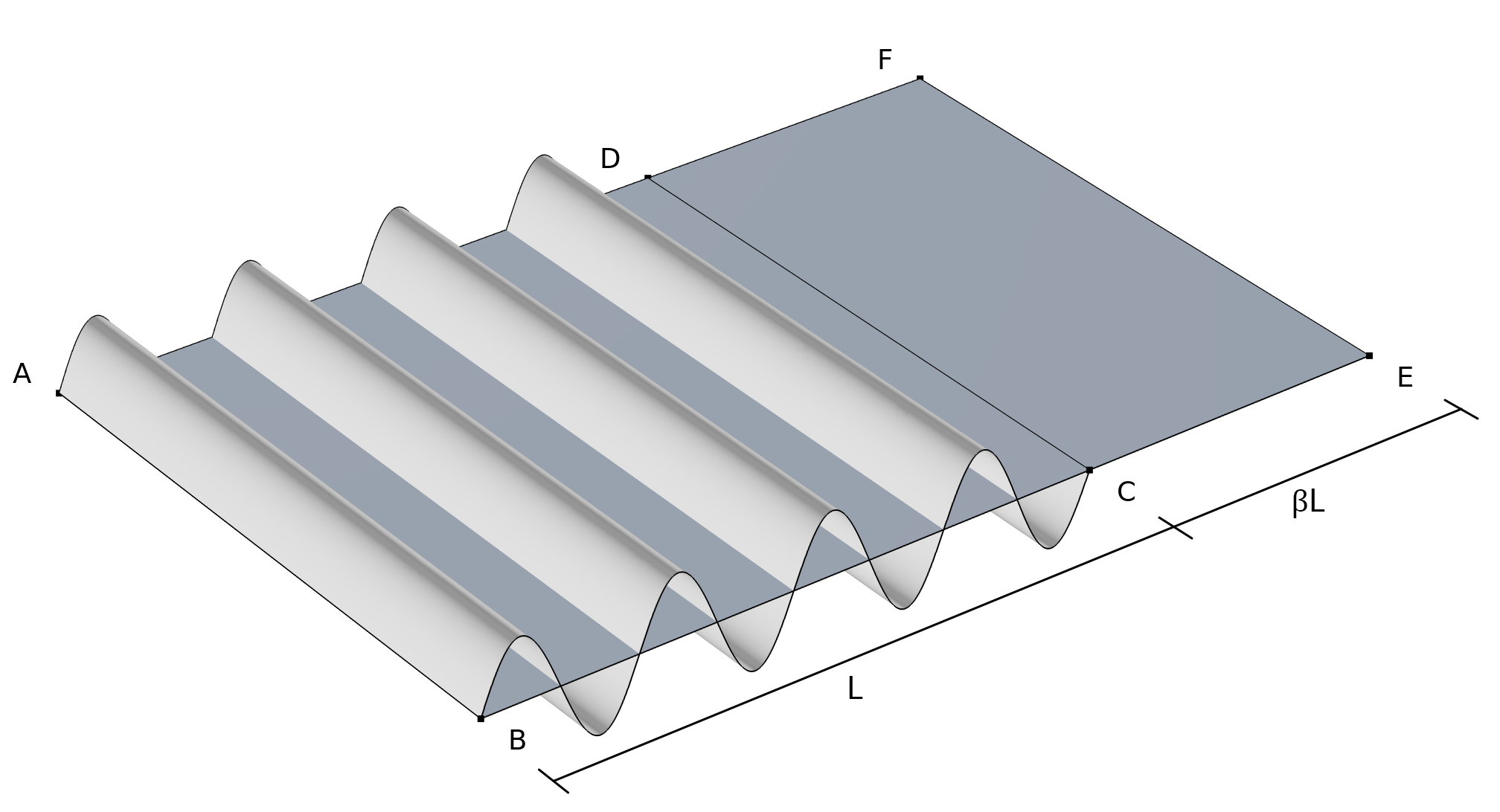
Kinematik der Faltenbildung. Die gekrümmte Fläche ABCD steht für die gefaltete Konfiguration, die ebene Fläche ABCD für die mittlere Konfiguration und die ebene Fläche ABEF für die verlängerte Konfiguration.
Für die faltige Membran zeigt die obige Abbildung drei verschiedene kinematische Beschreibungen:
- Der Verformungstensor \widetilde{\bf{F}} bildet die Referenzkonfiguration auf eine echte faltige Konfiguration (gekrümmte Fläche ABCD) ab.
- Nicht geeignet für die Bestimmung des Dehnungsfeldes in der faltigen Membran
- Der Verformungstensor \bf{F} bildet die Referenzkonfiguration auf eine mittlere Konfiguration (ebene Fläche ABCD) ab, bei der die Fläche kleiner ist als die tatsächliche Faltenfläche.
- Nicht geeignet für die Bestimmung des Dehnungsfeldes in der faltigen Membran
- Der Verformungstensor \bar{\bf{F}} bildet die Referenzkonfiguration auf eine fiktive verlängerte Konfiguration (ebene Fläche ABEF) ab, wobei die Fläche der tatsächlichen Faltenfläche entspricht.
- Geeignet zur Bestimmung des Dehnungsfeldes in der faltigen Membran
Unter der Annahme, dass die Faltenbildung in der \bf{n}_2-Richtung erfolgt und dass \bf{n}_1 die Richtung der einachsigen Spannung ist, ist \bar{\bf{F}} der modifizierte Verformungstensor und lautet
wobei \beta ein Parameter für Dehnung und Faltenbildung ist (Ref. 1). Das Symbol \otimes bezeichnet das äußere (dyadische) Produkt zweier Vektoren, das einen Tensor ergibt. \beta=0 steht für eine Straffungsbedingung. Gemäß der Orthogonalitätsbedingung und der Spannungsfeldtheorie ist
wobei \bf{\sigma} die Cauchy-Spannung ist. Sie wird in Form der zweiten Piola-Kirchhoff-Spannung geschrieben als
Unter der Annahme, dass die mittlere Konfiguration bekannt ist (\bf{F}), sind die einzigen Unbekannten \bf{n}_2 und \beta.
Nun wollen wir diese Gleichungen auf die Referenzkonfiguration übertragen, was praktischer ist, da die Kinematik und die Materialeigenschaften der Membran in der Referenzkonfiguration liegen. Wir nehmen an, dass \bf{h} ein Vektor in der Referenzkonfiguration ist, der dem Vektor \bf{n}_2 entspricht. Der fiktive Green-Lagrange-Dehnungstensor \bar{\bf{E}} wird also geschrieben als
wobei \bf{C} der mittlere rechte Cauchy-Tensor, \bf{N}_2 der Einheitsvektor in der Referenzkonfiguration und \beta^* der neue Faltungsparameter ist.
Die Membranoberfläche wird von einem Koordinatensystem aufgespannt, das zwei in der Ebene orthogonale Einheitsvektoren hat, \bf{e}_1 und \bf{e}_2. \bf{N}_1 und \bf{N}_2 werden in Bezug auf den Winkel \alpha geschrieben als
Die beiden nichtlinearen gekoppelten Gleichungen, die für zwei Unbekannte, \alpha und \beta^*, zu lösen sind, lauten
Diese beiden nichtlinearen algebraischen Gleichungen können mit dem Newton-Raphson-Verfahren gelöst werden:
f_{1,\alpha} & f_{1,\beta^*}\\
f_{2,\alpha} & f_{2,\beta^*}
\end{pmatrix} \begin{pmatrix}
\Delta \alpha\\
\Delta \beta^*
\end{pmatrix} = \begin{pmatrix}
-f_1\\
-f_2
\end{pmatrix}.
Hier werden \alpha und \beta^* durch die Newton-Raphson-Methode auf lokaler Ebene an jedem Gaußpunkt für jede Iteration auf globaler Ebene gelöst.
Das Feature Wrinkling
Der modifizierte Ansatz des Verformungstensors ist im Unterknoten Wrinkling implementiert, der sich unter den Knoten Linear Elastic Material und Hyperelastic Material im Interface Membrane befindet. Der Unterknoten Wrinkling hat drei verschiedene Optionen für ein Abbruchkriterium der lokalen Newton-Raphson-Methode mit der Möglichkeit, die Toleranzen anzupassen.
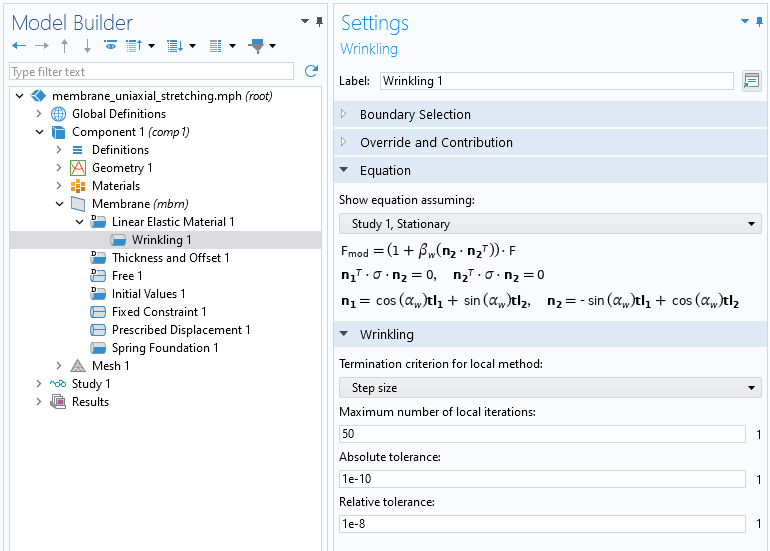
Der Unterknoten Wrinkling unter dem Feature Linear Elastic Material.
Es gibt mehrere Beispiele in der Application Gallery, die zeigen, wie man Faltenbildung mit Hilfe der integrierten Funktionalität des Interface Membrane modellieren kann. Das Modell Uniaxial Stretching of a Rectangular Membrane ist ein einfaches Modell, das leicht analytisch zu überprüfen ist. In diesem Beispiel werden die numerischen Ergebnisse mit den analytischen Ergebnissen verglichen, wie hier gezeigt:
Der faltige Bereich einer rechteckigen Membran ist in Dunkelrot dargestellt. In der Abbildung links wird ein isotropes Material verwendet, in der Abbildung rechts ein orthotropes Material. In beiden Abbildungen werden die analytischen Ergebnisse mit den berechneten (numerischen) Ergebnissen verglichen.
Das Modell Inflation of a Square Airbag ist praktischer und daher komplizierter. Das Modell zeigt die Faltenbildung in einem quadratischen Airbag mit einem linear elastischen Material beim Aufblasen. Ein ähnliches Modell, Inflation of a Square Hyperelastic Airbag, verwendet ein hyperelastisches Material.
Quadratischer Airbag, modelliert mit einem linear elastischen Material. Der faltige Bereich ist in Dunkelrot dargestellt.
Ein weiteres Beispiel für die Verwendung der integrierten Funktionen des Interface Membrane zur Analyse der Faltenbildung ist das Modell Torsion of a Circular Membrane, bei dem ein Drehmoment nur auf die Innenkante eines Rings ausgeübt wird, um Falten zu erzeugen. In diesem Beispiel wird die Auswirkung verschiedener Netzmuster und Diskretisierungen auf die Faltenbildung beobachtet.
Modifizierte Formulierung der konstitutiven Beziehung
Wie oben beschrieben, verwendet der Unterknoten Wrinkling in COMSOL Multiphysics® die modifizierte Formulierung des Verformungstensors. Dank der Flexibilität der Software ist es jedoch auch möglich, die Faltenbildung mit dem zweiten Ansatz zu modellieren: der Modifizierung der konstitutiven Beziehung.
In dieser zweiten Formulierung wird die konstitutive Beziehung für den faltigen Bereich angepasst. Die für den faltigen Bereich verwendete Dehnungsenergie wird als relaxierte Dehnungsenergie bezeichnet, während die im gespannten Bereich verwendete Dehnungsenergie als volle Dehnungsenergie bezeichnet wird. Dieser Ansatz ist auf alle isotropen hyperelastischen Materialmodelle anwendbar, der Einfachheit halber wird hier jedoch ein inkompressibles Neo-Hooke-Material betrachtet. Die volle Dehnungsenergiedichte in Bezug auf die Hauptdehnungen \lambda_1 und \lambda_2 wird geschrieben als
Die Cauchy-Hauptspannung \sigma ist gegeben durch
Die Cauchy-Hauptspannung in jeder Richtung ist gegeben durch
Nehmen wir an, dass die Dehnung in der ersten Hauptrichtung und die Faltenbildung in der zweiten Hauptrichtung erfolgt. Dann muss die folgende Gleichung im Faltenbereich gelten:
Mit dieser Gleichung wird ein Zustand uniaxialer Spannung im Faltenbereich hergestellt und die Spannung in Faltenrichtung wird Null. Ausgehend von der Nullspannung in Faltenrichtung ergibt sich die Faltungsbedingung in Bezug auf die Hauptdehnungen:
Der Faltenbereich wird also durch die folgende Ungleichung bestimmt: \lambda_2 \sqrt{\lambda_1} < 1. Setzt man die Faltungsbedingung, die sich aus den Hauptdehnungen ergibt, in die volle Dehnungsenergie ein, so lautet die relaxierte Neo-Hooke-Dehnungsenergie
Die relaxierte Dehnungsenergie ist nicht von der Dehnung in Faltenrichtung abhängig; das bedeutet, dass die Cauchy-Spannung in dieser Richtung automatisch Null wird.
Unter Verwendung der Faltungsbedingung und der obigen Energiedichten wird die Dehnungsenergiedichte für die gespannten und faltigen Bereiche angegeben als
Für isotrope Membranen kann die Gleichwertigkeit des modifizierten Verformungstensors und der modifizierten Formulierungen der konstitutiven Beziehung nachgewiesen werden. (Siehe Ref. 1 für weitere Informationen). Der Ansatz der modifizierten konstitutiven Beziehung ist jedoch nur auf isotrope Membranen anwendbar, während der Ansatz des modifizierten Verformungstensors allgemeiner ist und auch für anisotrope Membranen gilt.
Vergleich der Formulierungen in COMSOL Multiphysics®
In dem Tutorial-Modell Wrinkling of Cylindrical Membranes with Varying Thickness werden beide Formulierungen verglichen und die Ergebnisse als übereinstimmend befunden. Bei diesem Modell wird die zylindrische Membran zunächst axial gedehnt und dann mit Wasserdruck aufgeblasen. Während des Aufblasens werden die Außenkanten fixiert.
In COMSOL Multiphysics® kann die modifizierte Formulierung der konstitutiven Beziehung durch Auswahl der Option User Defined des Features Hyperelastic Material implementiert werden. Beachten Sie, dass die Dehnungsenergien des Neo-Hooke-Materials in diesem Tutorial-Modell speziell für eine inkompressible isotrope Membran geschrieben wurden. In einem solchen Fall sollte die integrierte Inkompressibilitätsformulierung nicht verwendet werden, da sie zusätzliche Terme hinzufügt, die einen Konflikt verursachen könnten. Sie können stattdessen die Option Compressible im benutzerdefinierten hyperelastischen Material verwenden, die die angegebene Dehnungsenergiedichte genau wie geschrieben verwendet.
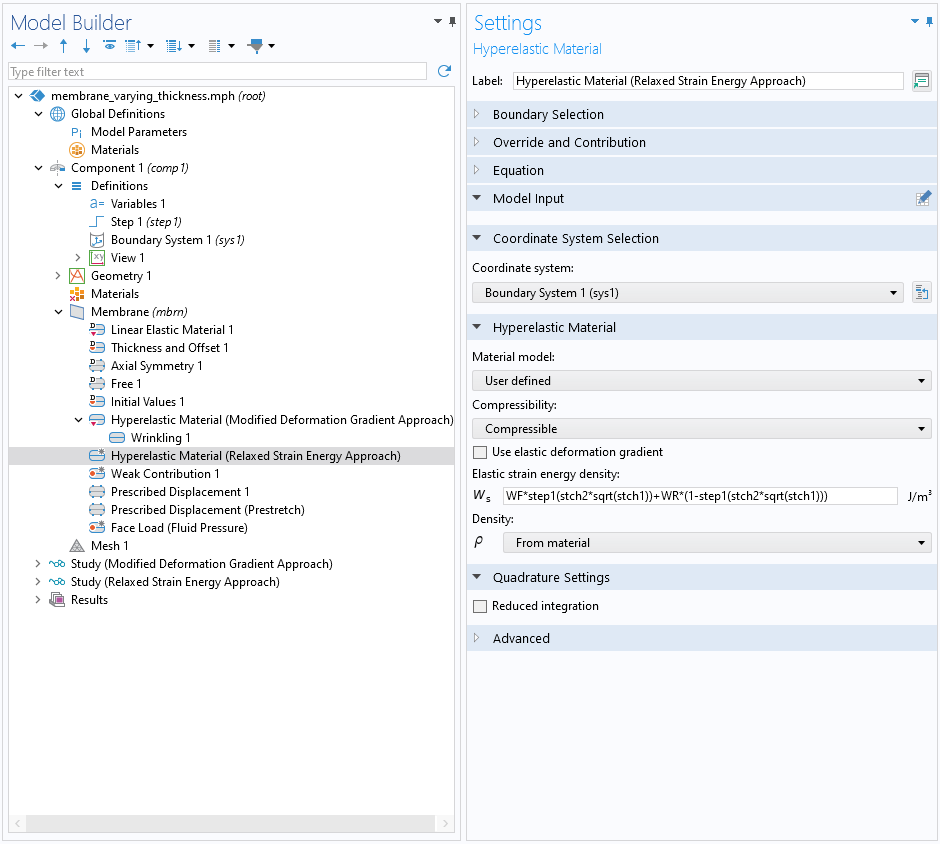
Der Unterknoten Wrinkling (der die modifizierte Formulierung des Verformungstensors verwendet) und ein benutzerdefiniertes hyperelastisches Materialmodell (das die modifizierte Formulierung der konstitutiven Beziehung verwendet).
Die folgenden Abbildungen zeigen den faltigen Bereich einer zylindrischen Membran bei unterschiedlichen Wasserhöhen nach beiden Modellierungsansätzen. Die dargestellten Ergebnisse zeigen, dass beide Ansätze im Wesentlichen gleichwertig sind und zu denselben Ergebnissen führen.
Der faltige Bereich einer zylindrischen Membran ist in Dunkelrot dargestellt. Links wurde der Ansatz des modifizierten Verformungstensors und rechts der Ansatz der modifizierten konstitutiven Beziehung verwendet. Die Beschriftung zeigt verschiedene Fluid-Höhen in der Membran, die 80 mm hoch ist und einen Radius von 10 mm hat.
Modellierung mit dem Interface Shell
Die Behandlung der Faltenbildung bei Verwendung des Interface Shell basiert auf der Bifurkationsanalyse. Faltenbildung wird als lokales Knickphänomen aufgrund der Druckspannungen betrachtet; daher ist eine Post-Buckling-Analyse zur Modellierung der Faltenbildung erforderlich. Der Vorteil der Post-Buckling-Analyse liegt in der Möglichkeit, die Wellenlängen und Amplituden der Faltenbildung zu bestimmen. Der erste Schritt bei der Behandlung der Faltenbildung ist eine vorgespannte Eigenwertanalyse, bei der die potenziellen Knickmoden ermittelt werden. Anschließend werden die wenigen ausgewählten Knickmoden mit der richtigen Skalierung als geometrische Unvollkommenheit für die Post-Buckling-Analyse verwendet.
Im Modell Uniaxial Stretching of a Rectangular Sheet wird das Auftreten von Falten in einem dünnen rechteckigen Blech mit Hilfe der Post-Buckling-Analyse von Schalen untersucht. Der folgende Screenshot zeigt den Modellbaum mit den für diese Analyse benötigten Knoten.
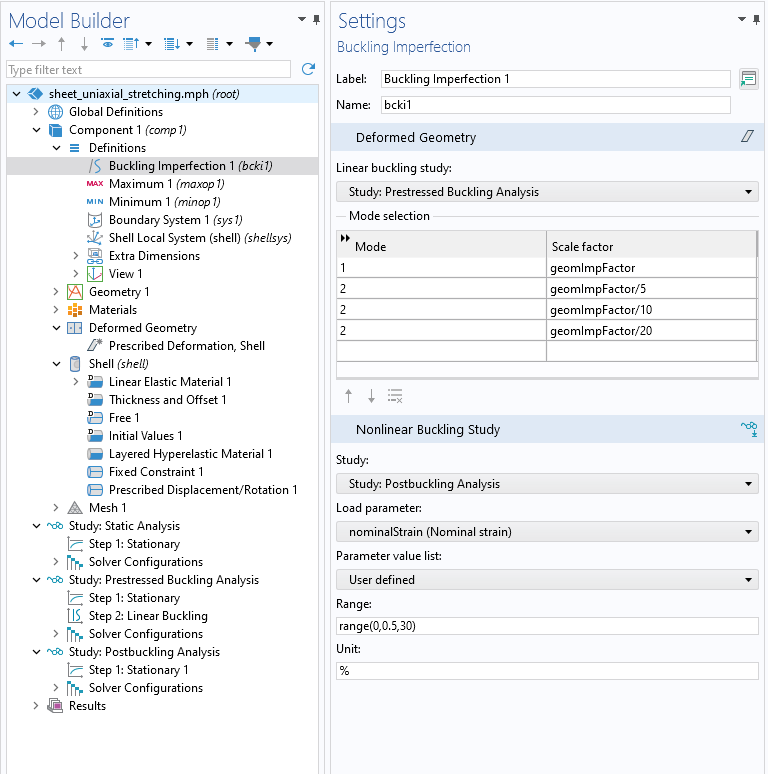
Der Knoten Buckling Imperfection und die erforderlichen Studien für das Modell Uniaxial Stretching of a Rectangular Sheet.
Der erste Schritt dieses Tutorial-Modells besteht in der Identifizierung potenzieller Faltenbereiche durch eine statische Analyse. In dieser Phase wird das rechteckige Blech einer uniaxialen Dehnung unterzogen. Ziel ist es, den Bereich zu finden, in dem die zweite Hauptspannung in eine Druckspannung übergeht. Anschließend wird eine vorgespannte Knickanalyse unter Verwendung der Untersuchungsschritte Stationary und Linear Buckling durchgeführt.
Für die Post-Buckling-Analyse können Sie den Knoten Buckling Imperfection verwenden, wie im obigen Screenshot dargestellt. Innerhalb dieses Knotens haben Sie die Möglichkeit, die gewünschte Anzahl von Knickmoden und ihre entsprechenden Skalierungsfaktoren auszuwählen. Diese skalierten Moden werden dann kombiniert und als geometrische Imperfektion für die Post-Buckling-Analyse verwendet. Über den Knoten Buckling Imperfection können Sie auch eine parametrische nichtlineare Knickstudie erstellen.
Die Animation unten zeigt die Faltenbildung in einem rechteckigen Bogen bei zunehmender uniaxialer Dehnung, während die zweite Abbildung die Amplitude der Falten entlang der Mittellinie in der Faltenrichtung zeigt. Zu Beginn, wenn die Dehnung des rechteckigen Bogens erhöht wird, beginnen sich Falten zu bilden. Die Faltenamplitude nimmt mit zunehmender Dehnung zu, bis sie einen kritischen Wert erreicht, nach dem sie abzunehmen beginnt. Bei einem bestimmten Dehnungswert wird die Faltenamplitude sehr klein.
Falten in einer Post-Buckling-Analyse. Das Farbschema zeigt die Faltenamplitude, wobei Blau für den negativen Bereich, Rot für den positiven Bereich und Grün für die Nullverschiebung steht.
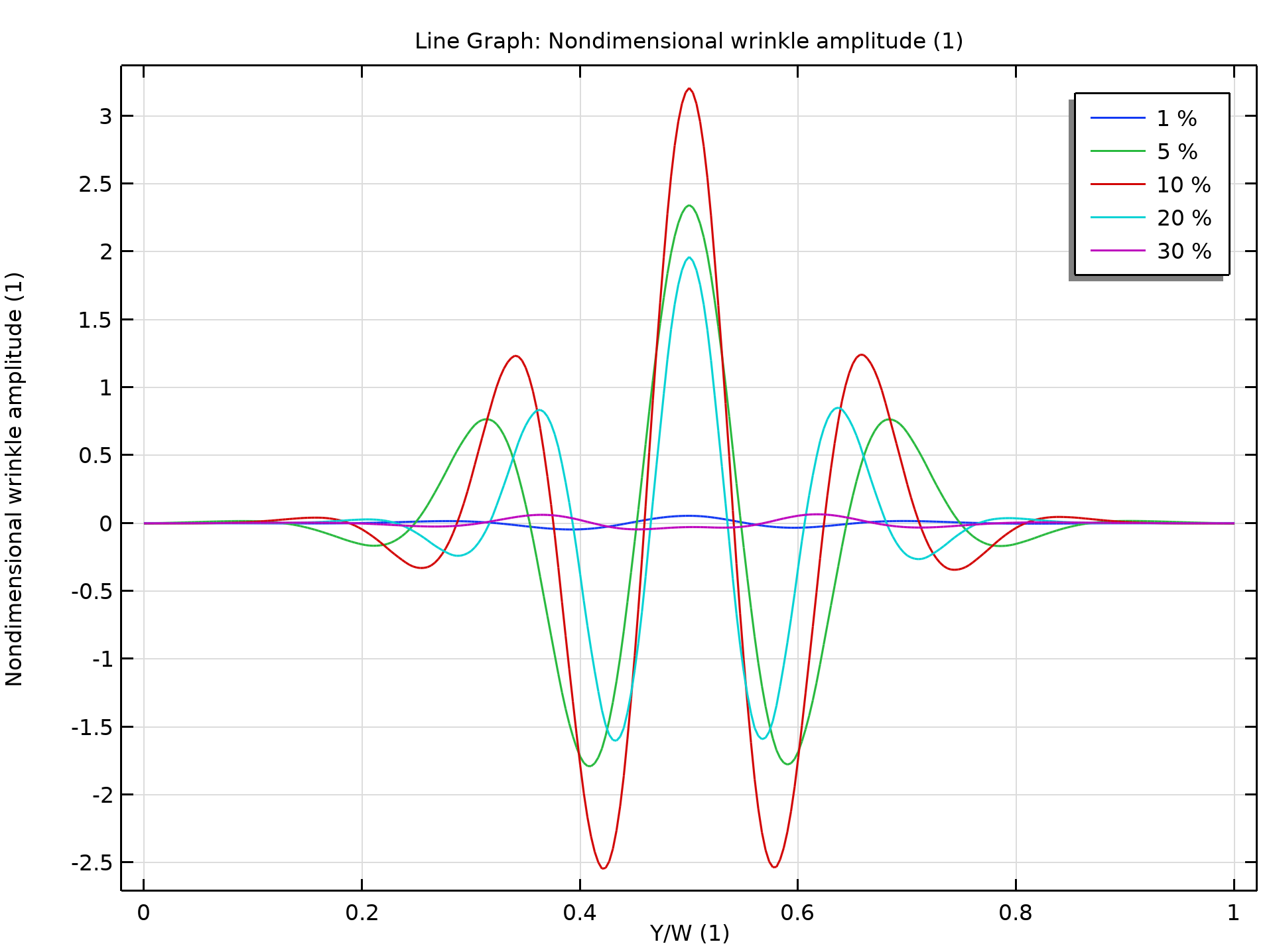
Faltenamplitude in einer Post-Buckling-Analyse.
Schlussbemerkungen
Wie wir gezeigt haben, kann Faltenbildung in COMSOL Multiphysics® mit den Interfaces Membrane und Shell modelliert werden. Die Membrananalyse der Faltenbildung kann durch Modifikation des Verformungstensors oder der konstitutiven Beziehung durchgeführt werden. Die Membrananalyse ist schnell und numerisch effizient und bietet eine korrekte Identifizierung der Faltenbereiche und der Spannungsverteilung. Allerdings liefert sie keine Informationen über Faltenamplituden und Wellenlängen. Die Schalenanalyse der Faltenbildung hingegen ist zeitaufwändig, numerisch anspruchsvoll und reagiert empfindlich auf die Eingabe geometrischer Mängel. Sie liefert jedoch wertvolle Daten zu Faltenamplituden und Faltenwellenlängen und ermöglicht zudem eine korrekte Vorhersage der Spannungsverteilung und der Faltenbereiche. Da beide Analysen ihre jeweiligen Vor- und Nachteile haben, können Ingenieure je nach den spezifischen Modellierungsanforderungen eine der beiden Arten wählen.
Referenzen
- A. Patil, Inflation and Instabilities of Hyperelastic Membranes, PhD thesis, Royal Institute of Technology (KTH), Stockholm, 2016.
- H. Schoop et al., “Wrinkling of nonlinear membranes,” Computational Mechanics, vol. 29, pp. 68–74, 2002; https://doi.org/10.1007/s00466-002-0326-y





Kommentare (0)