Spannungsminimierung: Ein heuristischer Ansatz zur Verbesserung des Ermüdungsverhaltens

Viele Metriken zur Ermüdungsevaluation basieren auf der Spannungsevaluation, sind jedoch nicht mit Hochleistungsoptimierungsmethoden wie der gradientenbasierten Optimierung kompatibel. Dies macht es schwierig, die Ermüdungsleistung durch die direkte Anwendung von Optimierungsmethoden zu verbessern. Dieser Blog-Beitrag zeigt, wie die Spannungsminimierung als heuristischer Ansatz zur Verbesserung des Ermüdungsverhaltens eingesetzt werden kann. Die Methode beruht auf einer gradientenbasierten Optimierung, um Tausende von Designvariablen zu verbessern und gleichzeitig die Masse- und Steifigkeitseigenschaften des Designs beizubehalten.

Ermüdung

Wenn ein Bauteil wiederholter Belastung ausgesetzt ist, können sich kleine Risse im Material bilden. Diese Risse können dann mit jedem Belastungszyklus wachsen, bis die Ausbreitung in eine schnelle Phase eintritt, die zum endgültigen strukturellen Versagen des Bauteils führt. Dieser Prozessablauf von Initiierung, Ausbreitung und endgültigem Versagen definiert den Ermüdungsbruchprozess. In den meisten praktischen Situationen besteht das Ziel darin, die Rissbildung insgesamt zu verhindern, da die Kontrolle der Ausbreitungsphase nach der Rissbildung eine enorme Herausforderung darstellt. Eine Ermüdungsanalyse soll die Anzahl der Lastzyklen berechnen, die das Bauteil bis zu diesem Zeitpunkt aushalten kann. Dies definiert die Ermüdungslebensdauer.

Die de Havilland Comet war ein Flugzeug, das aufgrund von Ermüdungsrissen, die an gestanzten Nietlöchern in der Nähe der Fenster entstanden waren, mitten im Flug auseinander brach. Um dies in Zukunft zu verhindern, wurden bei späteren Versionen des Flugzeugs geklebte Fenster verwendet. Bild von Completeaerogeek. Lizenziert unter CC BY-SA 4.0 über Wikimedia Commons.

Die Entstehung von Ermüdungsrissen hängt von der Belastung des Bauteils und den durch die Belastung entstehenden Spannungen ab. Ermüdungsrisse, deren Entstehung maßgeblich durch die wiederholte Belastung begünstigt wird, können bei Spannungswerten weit unterhalb der Fließspannung des Materials entstehen. Für das Design kann es jedoch sinnvoll sein, das zyklische Verhalten der Belastung zu vernachlässigen und stattdessen einen statischen Lastfall zu betrachten, um Bereiche mit hohen Spannungen zu identifizieren.

Spannungsminimierung

Die Minimierung der maximalen Spannung wird in der Strukturmechanik häufig angestrebt, doch solche Optimierungsprobleme sind in der Praxis schwer zu lösen, da sich die genaue Position der maximalen Spannung während der Optimierung ändern kann. Daher werden oft Spannungsaggregationsverfahren eingesetzt, die die maximale Spannung annähern, wobei die Verwendung einer p-Norm der von-Mises-Spannung weit verbreitet ist:

Die Genauigkeit der Annäherung verbessert sich mit p\rightarrow\infty, jedoch führt dies auch zu einer abrupteren Veränderung des Gradienten, was numerische Probleme verursacht. Dementsprechend werden nur selten Werte über 10 für die Topologieoptimierung verwendet. Dieser Beitrag konzentriert sich jedoch auf die Formoptimierung, bei der teilweise Werte bis zu 50 verwendet werden können, ohne dass numerische Probleme auftreten. Die ungefähre maximale Spannung, \sigma_\mathrm{max}, und Varianten davon können verwendet werden, um die Spannung bei der Form- und Topologieoptimierung einzuschränken, wie in der COMSOL Application Gallery (zum Beispiel in den Modellen Optimizing a Flywheel Profile und Topology Optimization of Loaded Knee Structure with a Maximum Stress Constraint) gezeigt wird. In den folgenden Beispielen zeigen wir, dass dieses Ziel als heuristischer Ansatz zur Formoptimierung in Bezug auf das Ermüdungsverhalten verwendet werden kann.

Ergebnisse für eine Halterung

Das erste Beispiel ist eine Halterungsgeometrie, die zur Veranschaulichung verschiedener Konzepte in der Strukturmechanik verwendet wird. (Weitere Informationen finden Sie beim Modell Bracket — Stress Optimization with Fatigue Evaluation.) Im folgenden Bild sind die Lasten und Randbedingungen zusammen mit der Spannungsverteilung dargestellt. An den festen Löchern werden Federn verwendet, um künstliche Spannungskonzentrationen zu vermeiden. Alternativ kann das Modell um die Schrauben erweitert werden.

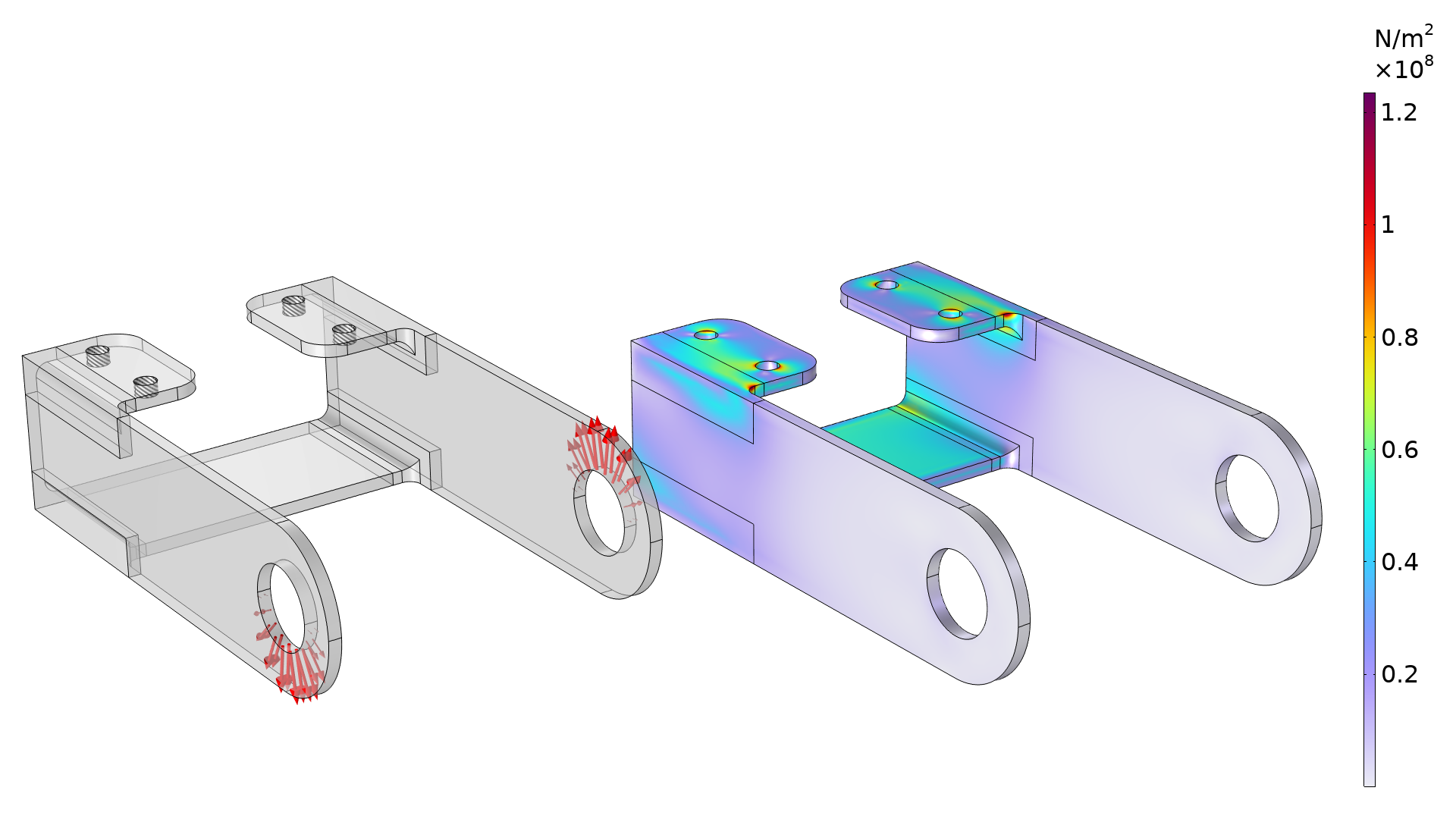
Der Plot zeigt die Randbedingungen (links) und die anfängliche Spannungsverteilung (rechts). Die Spannung tritt konzentriert in der Nähe der Verrundungen oben in der Halterung auf.

Die Optimierung verwendet die p-Norm (p=50) aus dem vorherigen Abschnitt als Zielfunktion, aber es werden auch Einschränkungen hinzugefügt, um eine schwerere oder weniger steife Struktur zu vermeiden. Die hier betrachteten 3D-Beispiele verwenden das Feature Free Shape Boundary, doch die Software COMSOL Multiphysics^® verfügt über eine Vielzahl weiterer integrierter Features zur Formoptimierung, wie in unserem Blog-Beitrag „Shape Optimization in Electromagnetics: Part 1“ gezeigt wird. Durch die Verwendung des Features Free Shape Boundary wird die Form der problematischen Verrundung geändert, um die Spannungskonzentration zu reduzieren, was die Ermüdungseigenschaften verbessert (siehe nachfolgende Abbildung).

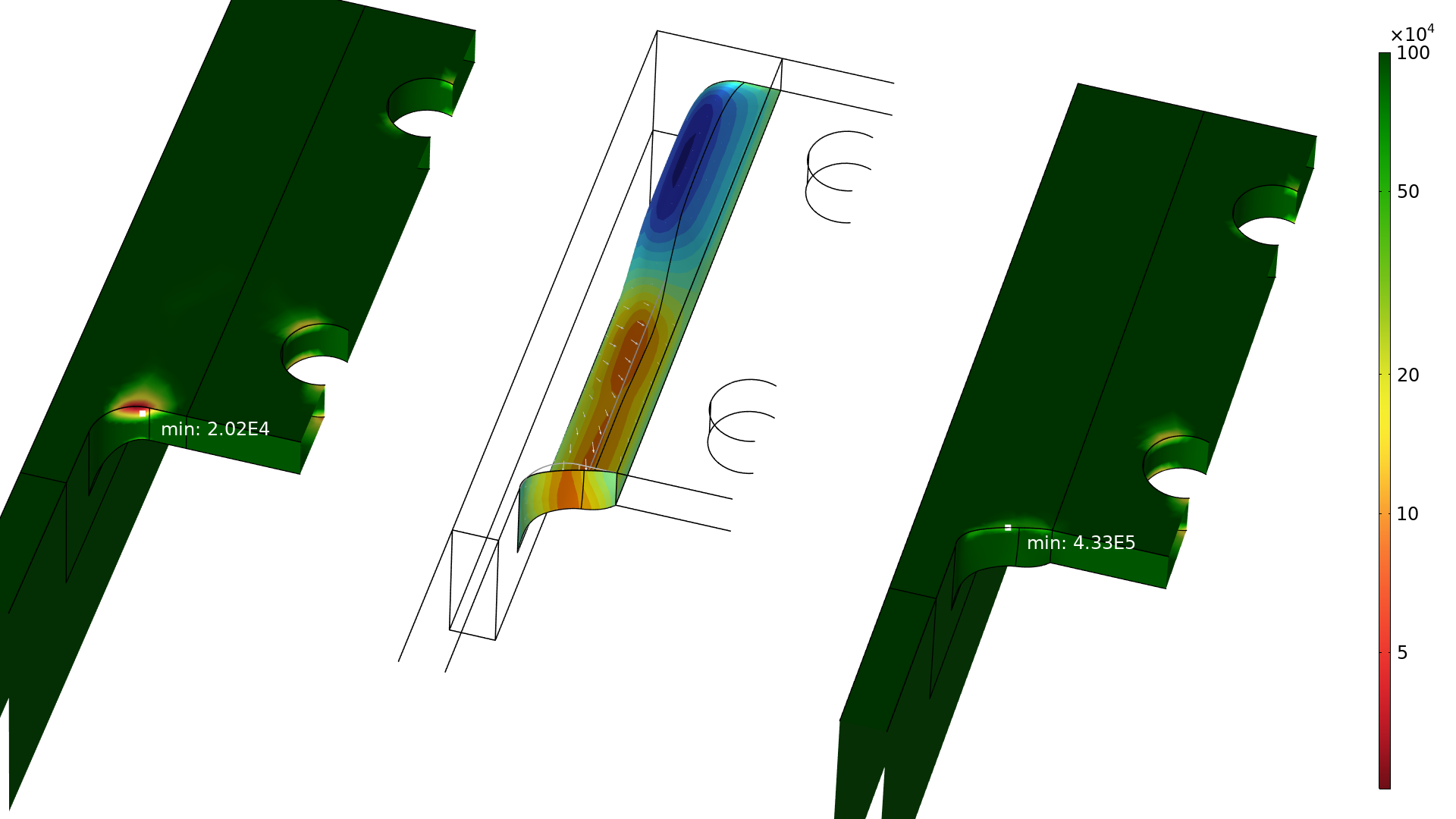
Die Anzahl der Zyklen bis zum Versagen ist für Ausschnitte des ursprünglichen und des optimierten Designs (links bzw. rechts) als Plot dargestellt. Die Formänderung wird auch durch Pfeile im mittleren Ausschnitt veranschaulicht, wobei die blauen und roten Bereiche der Entfernung bzw. dem Hinzufügen von Material entsprechen.

Im Allgemeinen versagt ein Bauteil, sobald ein Teil davon seine Ermüdungslebensdauer überschritten hat. Daher ist die Mindestanzahl von Zyklen bis zum Versagen die relevanteste Zahl. Idealerweise würde diese Zahl direkt als Ziel verwendet werden, doch es besteht eine gute Übereinstimmung zwischen dieser Zahl und dem p-Norm-Ziel, wie in der folgenden Grafik zu sehen ist.

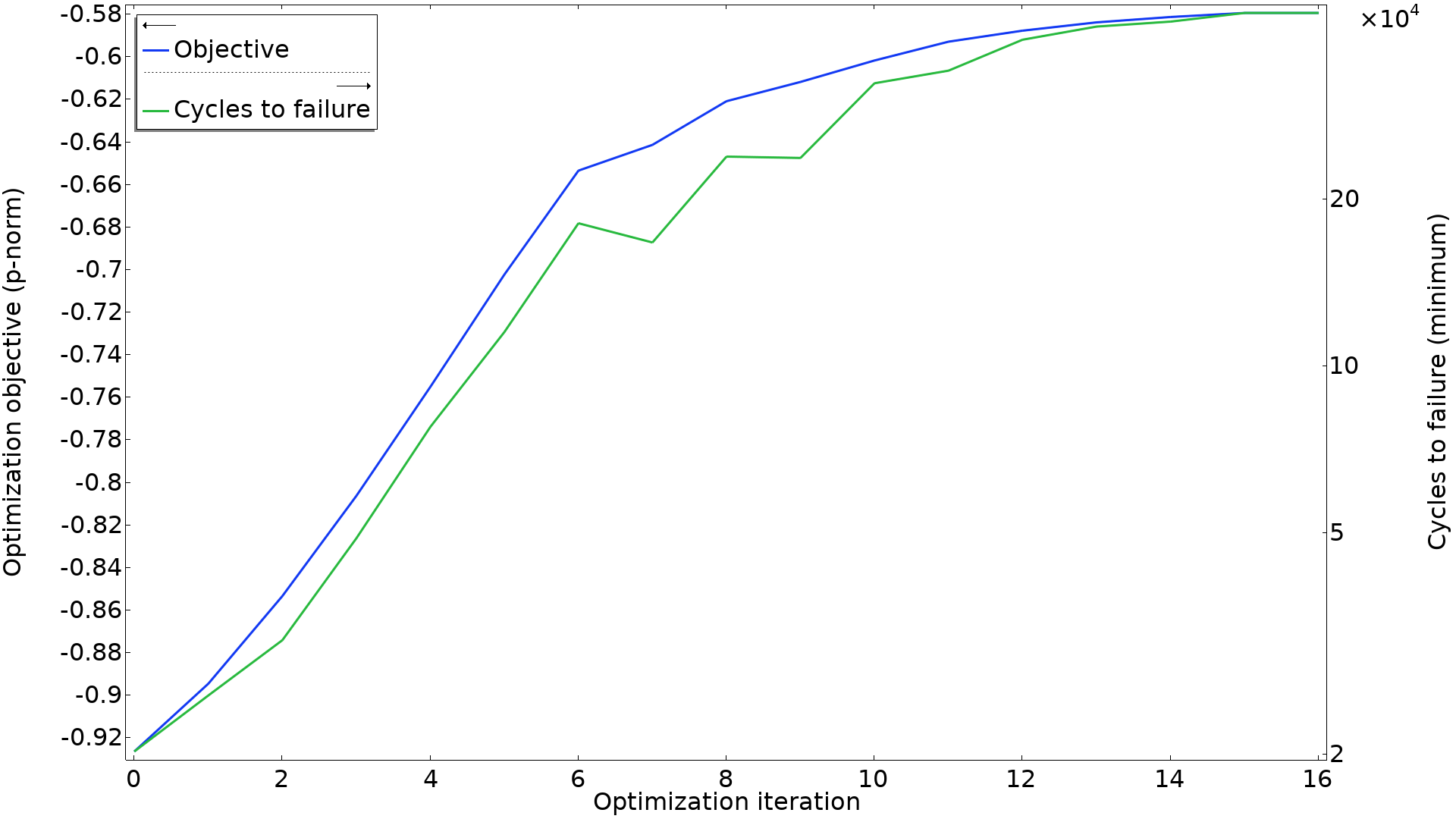
Das Ziel der p-Norm wird zusammen mit der Mindestanzahl der Zyklen bis zum Versagen als Plot dargestellt. Einige Iterationen verbessern die p-Norm, ohne die Mindestanzahl der Zyklen bis zum Versagen zu verbessern, doch es besteht eine gute Korrelation zwischen den beiden.

Von-Mises-Spannung und Ermüdungslebensdauer

Wie lässt es sich erklären, dass eine reine von-Mises-Spannungsminimierung so gut mit einer Verbesserung der Ermüdungslebensdauer korreliert? Die Ermüdungslebensdauer eines Bauteils wird von vielen Faktoren beeinflusst, wobei die Spannungsamplitude am meisten dazu beiträgt. Auch die mittlere Spannung ist ein wichtiger Faktor. Häufig sind die Lasten vollständig umgekehrt, und dann ist die mittlere Spannung überall gleich Null.

In der Regel entstehen Ermüdungsrisse an einer freien Oberfläche an einer Spannungskonzentration. An einer freien Oberfläche dominiert ein Zustand der ebenen Spannung, in der Praxis ist der Spannungszustand jedoch oft nahezu uniaxial. Dies bedeutet zum Beispiel, dass die erste Hauptspannung und die von-Mises-Vergleichsspannung gleich sind.

Bei der Kombination eines statischen Lastfalls, der eine mittlere Spannung erzeugt, und eines weiteren Lastfalls für die pulsierende Last ist dieser Ansatz nicht unbedingt optimal. Aber selbst dann besteht eine große Erfolgschance, da bei einer Spannungskonzentration verschiedene Arten von externen Lasten häufig zu ähnlichen Spannungsmustern führen.

Ergebnisse für ein Rad

Das zweite Beispiel ist eine Felge aus dem Modell Wheel Rim — Stress Optimization with Fatigue Evaluation. Dieses Modell ist konzeptionell identisch mit der Halterung, mit Ausnahme von vier Punkten:

1. Es gibt mehrere Lastfälle und die Ermüdungsanalyse sucht nach der schlechtesten Kombination (unter Verwendung des Findley-Kriteriums), sodass eine schwächere Beziehung zur maximalen Spannung erwartet wird.
2. Die Tatsache, dass es mehr Lastfälle gibt, führt auch zu mehr Beschränkungen.
3. Die Sektorsymmetrie wird für die Formoptimierung (nicht die Physik) auferlegt.
4. Der Ermüdungsnutzungsfaktor wird in den Ergebnissen verwendet (anstelle der Ermüdungslebensdauer), und dies kann als reziproker Sicherheitsfaktor betrachtet werden.

Die Radgeometrie, die Einschränkungen und die Randbedingungen sind nachfolgend dargestellt. Für die Schrauben werden einfache feste Randbedingungen verwendet, die zu künstlichen Spannungskonzentrationen führen, sodass diese Bereiche von der Ermüdungsanalyse ausgeschlossen werden.

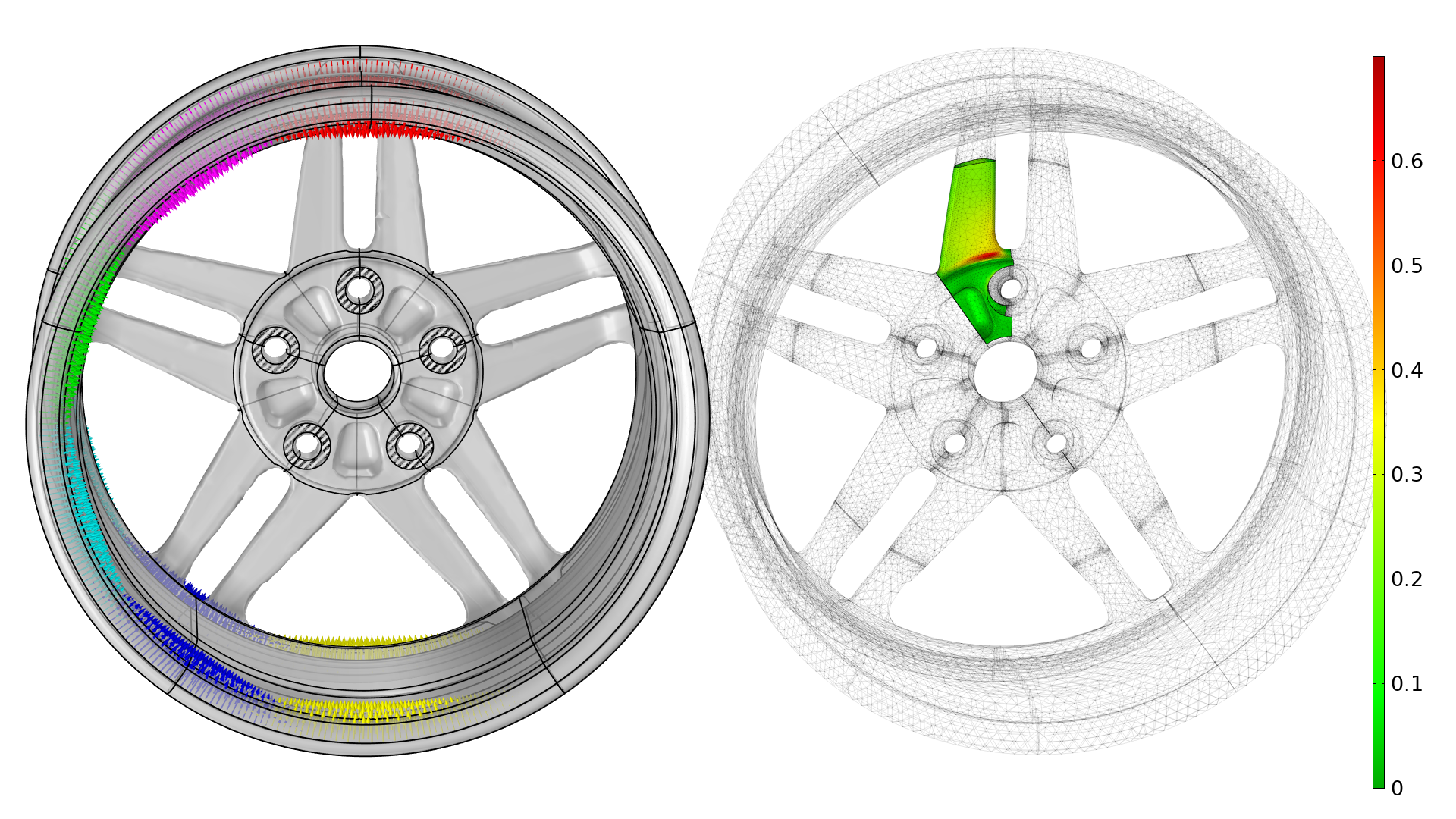
Die verschiedenen Lastfälle werden durch verschiedenfarbige Pfeile dargestellt (links). Der anfängliche Ermüdungsnutzungsfaktor ist rechts im Plot dargestellt, wobei dieser Plot alle Lastfälle berücksichtigt, entsprechend einer vollen Radumdrehung. Ein grobes Netz kann für die Speichen verwendet werden, jedoch nicht für die Ermüdungs- oder Spannungsbewertung. Das Rad ist auch einer Last durch den Luftdruck im Reifen ausgesetzt, dies ist jedoch in der Abbildung nicht dargestellt.

Die Optimierung verwendet weiterhin das Ziel der p-Norm (p=20) zusammen mit einer Beschränkung der Masse, aber dieses Beispiel berücksichtigt mehr Lastfälle, sodass es mehr Beschränkungen gibt. Die folgende Abbildung zeigt, wie die Optimierung durch Anpassung einer Verrundung die Ermüdungslebensdauer verbessert.

Der Ermüdungsnutzungsfaktor ist für Ausschnitte des ursprünglichen und des optimierten Designs (links bzw. rechts) als Plot dargestellt. Die Formänderung wird auch durch Pfeile im mittleren Ausschnitt veranschaulicht, wobei die grauen und schwarzen Linien die ursprüngliche bzw. die optimierte Geometrie darstellen.

In diesem Beispiel besteht auch eine gute Korrelation zwischen dem Ziel der p-Norm und der Mindestanzahl von Zyklen bis zum Versagen, wie in der folgenden Grafik zu sehen ist. Es ist erwähnenswert, dass zwei der Lastfälle in Bezug auf die p-Norm dominieren, aber alle Beschränkungen während der Optimierung aktiv bleiben.

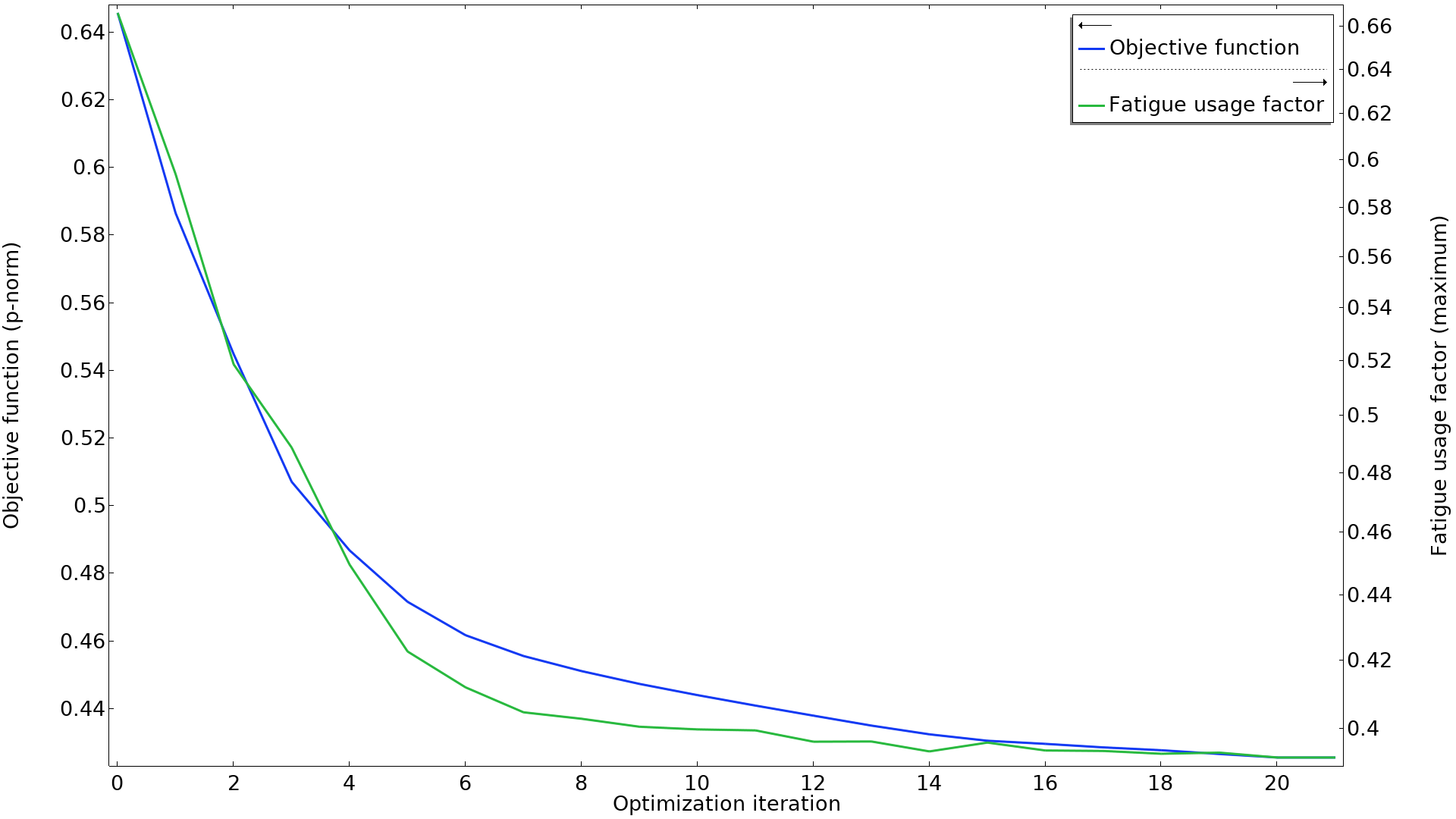
Das Ziel der p-Norm wird zusammen mit dem maximalen Ermüdungsnutzungsfaktor in einem Plot dargestellt. Die beiden Kurven scheinen gut miteinander zu korrelieren. Der Ermüdungsnutzungsfaktor wird auf einer logarithmischen Achse dargestellt.

Schlussbemerkungen

Die Optimierung der Ermüdungslebensdauer ist nicht einfach, aber es ist oft möglich, das Verhalten durch eine belastungsbasierte Formoptimierung zu verbessern. Die Optimierungsergebnisse sollten mit einer Ermüdungsanalyse überprüft werden. Anschließend kann das Optimierungsergebnis als Eingabe für die nächste Phase des Workflows verwendet werden.

In diesem Blog-Beitrag haben wir uns auf die Verwendung der p-Norm der von-Mises-Spannung als Ziel konzentriert. Da COMSOL Multiphysics^® jedoch automatisch die für die gradientenbasierte Optimierung erforderliche Sensitivitätsanalyse durchführt, ist es einfach, mit alternativen Zielen zu experimentieren.