
Beim Kauf eines neuen Autos tragen die Geräusche und Gefühle, die Sie beim Schließen der Autotür erleben, auf subtile, aber wichtige Weise zu Ihrem ersten Eindruck bei. Die Türen reagieren empfindlich auf Vibrationen, was je nach Design und Struktur unterschiedliche Geräusche beim Schließen der Türen verschiedener Autos verursacht. Es ist wichtig für das Fahrerlebnis, diese Vibrationen in den Türen reduzieren zu können. Bei hohen Geschwindigkeiten kann die Strömung Vibrationen in der Tür und den Seitenfenstern verursachen, die sich in die Kabine und sogar in die Innenverkleidung und andere Innenteile ausbreiten können, was zu störenden Geräuschen führt. Manche Menschen können allein durch das Geräusch eines losen Gurtschlosses, das während der Fahrt an der B-Säule vibriert, extrem frustriert werden. Ich kann mir nicht vorstellen, was passieren würde, wenn die Verkleidung Geräusche von sich gäbe!
Ein wichtiger Teil des Designs im Hinblick auf Vibrationen bei hohen Geschwindigkeiten ist die Aerodynamik eines Fahrzeugs. Mit Hilfe von Modellierung und Simulation lassen sich die Strömung und das Druckfeld um ein Fahrzeug mit solider Genauigkeit abschätzen. Der schwankende Druck, der durch die Strömung ausgeübt wird, kann in einer Strukturanalyse als Oberflächenlast verwendet werden. In diesem Zusammenhang ist es wichtig, dass die von der Luft bei hohen Geschwindigkeiten ausgeübten Kräfte nicht nur hinsichtlich ihrer Größe, sondern auch hinsichtlich ihrer Frequenz geschätzt werden.
In diesem Blog-Beitrag befassen wir uns mit der Verwendung von Modellen der Large-Eddy-Simulation (LES) zur Vorhersage der transienten Kräfte, die der Luftstrom bei hoher Geschwindigkeit auf die Tür und den Seitenspiegel eines Sportwagens ausübt. Diese Kräfte werden dann als Lasten in einer Strukturanalyse verwendet.
Warum ein Sportwagen? Weil es mehr Spaß macht, natürlich! Und da ich wahrscheinlich nie einen Supersportwagen besitzen werde, könnte mich das Modellieren eines solchen zumindest für eine Weile zufriedenstellen…

Der Lamborghini Miura® gilt als der erste Supersportwagen. Er wurde von 1966 bis 1973 produziert. Hier ist das Modell P400 von 1967 zu sehen. Rechts im Hintergrund sehen wir das Heck eines anderen klassischen Supersportwagens, des Ferrari® 512 BB aus dem Jahr 1972. Links im Hintergrund ist das Heck eines De Tomaso Mangusta® mit seinen klassischen Flügel-Heckfenstern zu sehen, der ebenfalls 1967 auf den Markt kam. Bild von joergens.mi — eigenes Werk. Lizenziert unter CC BY-SA 3.0, über Wikimedia Commons.
Anmerkung des Herausgebers: Lamborghini und Miura sind eingetragene Marken von Automibili Lamborghini S.p.A. De Tomaso Mangusta ist eine eingetragene Marke von De Tomaso Automobili Limited. Ferrari ist eine eingetragene Marke von Ferrari S.P.A. Es wird keinerlei Sponsoring, Billigung, Zugehörigkeit oder sonstige Verbindung zu den Eigentümern dieser Marken impliziert.
Das Large-Eddy-Simulationsmodell
Der Vorteil des LES-Modells besteht darin, dass es genaue Schätzungen der zeitlichen Fluktuation der Strömung liefern kann. Das bedeutet auch, dass es die Kräfte auf der Oberfläche der Fahrzeugkarosserie als Funktion der Zeit abschätzen kann. In der Strukturanalyse der Tür und des Spiegels wollen wir diese zeitlich schwankenden Kräfte als Lasten verwenden, indem wir diese Lasten mit Hilfe der Fast-Fourier-Transformation (FFT) in den Frequenzbereich transformieren. Dies soll zu einer Abschätzung des Risikos von Schwingungen in den Türen und Spiegeln führen, indem die durch die Lasten angeregten Eigenmoden betrachtet werden.
Das Strömungsfeld um die Türen und Spiegel hängt von der Form des Fahrzeugs ab. Um ein präzises Strömungsfeld zu erhalten, müssen wir das gesamte Auto modellieren. Außerdem macht es mehr Spaß, das ganze Auto zu modellieren, sofern wir uns den Rechenaufwand leisten können.
Die Analyse der Strömung ist etwas komplex, da wir geeignete Anfangsbedingungen für das LES-Modell benötigen. Dies beinhaltet die Lösung einer Laplace-Gleichung für die Potentialströmung, die Verwendung der Lösung der Potentialströmung als Anfangsbedingung für eine RANS-Simulation (Reynolds-gemittelte Navier-Stokes-Simulation) und dann wiederum die Verwendung der Ergebnisse der RANS-Simulation als Anfangsbedingung für das LES-Modell. Der erste Schritt wird durchgeführt, um die Anzahl der Iterationen für die RANS-Simulation zu reduzieren. In diesem Fall wollen wir nicht ein separates RANS-Interface und ein LES-Interface definieren, da sich dadurch die Anzahl der Freiheitsgrade verdoppeln würde, sondern wir ändern die Eigenschaften des RANS-Interface zu LES. Dies ist nicht die eleganteste Art und Weise, das Modell in der COMSOL Multiphysics® Software einzurichten, aber es ist die am wenigsten rechenintensive. Die folgende Abbildung zeigt den Modellbaum für das Strömungsmodell.
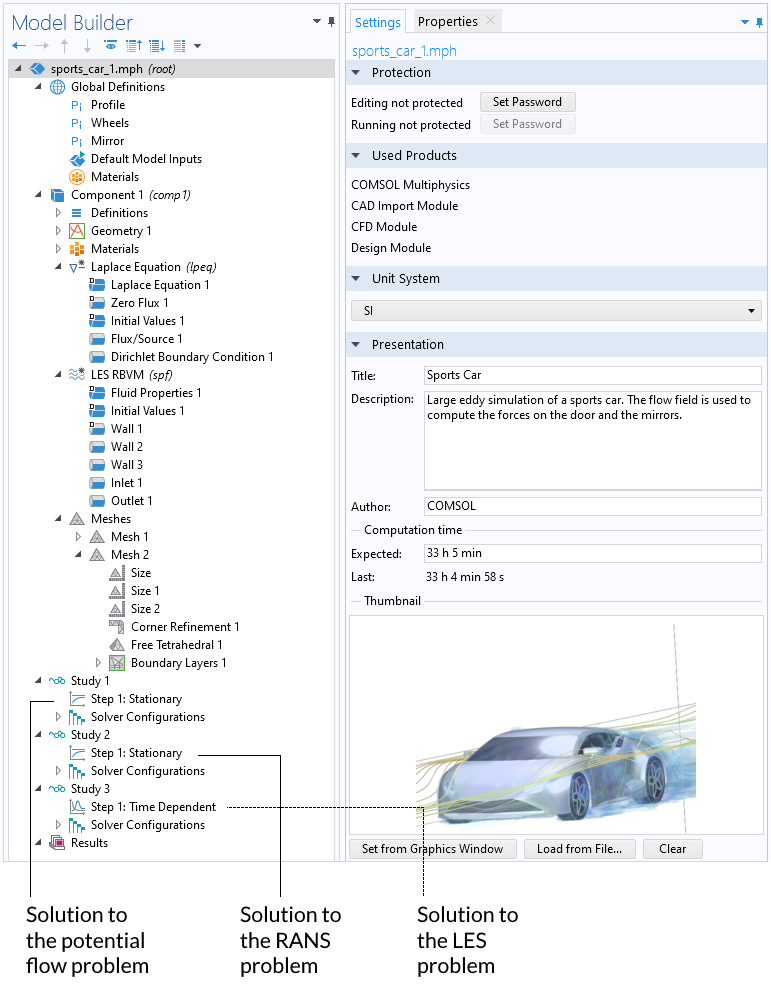
Der Modellbaum für das Problem der Strömung.
Der Begrenzungsrahmen für das luftgefüllte Gebiet um das Auto muss groß genug sein, damit wir hoffentlich etwas über die Strömung oder den Druck an den Rändern wissen, um die Randbedingungen zu definieren. Dies wiederum bestimmt, wie das Netz aussehen soll. Wir brauchen eine Randschicht um das Auto herum. Außerdem müssen wir auch ein gewisses Elementwachstum vom Auto weg zulassen, um die Größe des Problems zu reduzieren. Das Netz ist unten abgebildet.
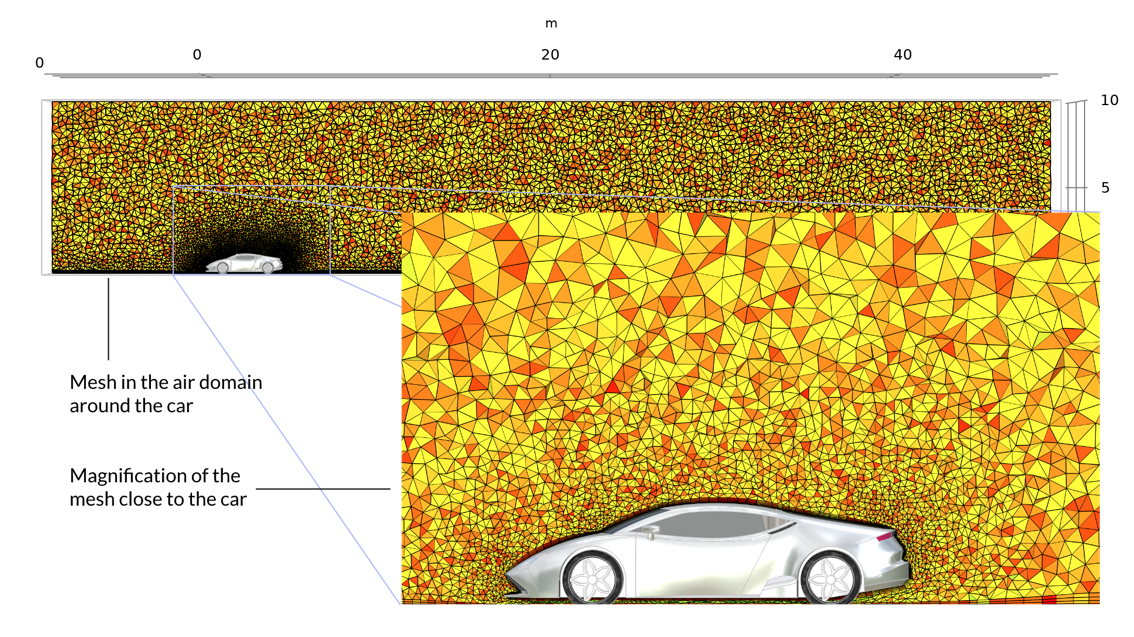
Das Netz im Luftgebiet und eine Vergrößerung dieses Netzes näher am Fahrzeug. An der Oberfläche des Fahrzeugs wird automatisch ein Netz für die Randschicht erstellt.
Die Abbildung unten zeigt die Strömung hinter dem Auto. Es ist zu erkennen, dass die Strömungsspur sehr weit hinter das Auto reicht. Diese Strömungsspur muss leiser und glatter werden, um eine Randbedingung hinter dem Auto zu schaffen; deshalb gibt es das sehr lange luftgefüllte Gebiet hinter dem Auto.

Die Störung im Strömungsfeld hinter dem Auto, das mit 180 km/h fährt, reicht sehr weit hinter das Auto, daher ist ein langes Luftgebiet erforderlich.
Die Bereiche um den Spiegel und den oberen Teil der Tür, das Seitenfenster, sind der größten relativen Strömung ausgesetzt. Die Abbildung unten zeigt die Strömung von vorne und hinten mit einer Vergrößerung der Bereiche um die Seitentür. Der Luftwiderstandsbeiwert dieses selbst gebauten Autos wird vom Modell mit 0,19 berechnet, was ein niedriger, aber realistischer Wert ist.
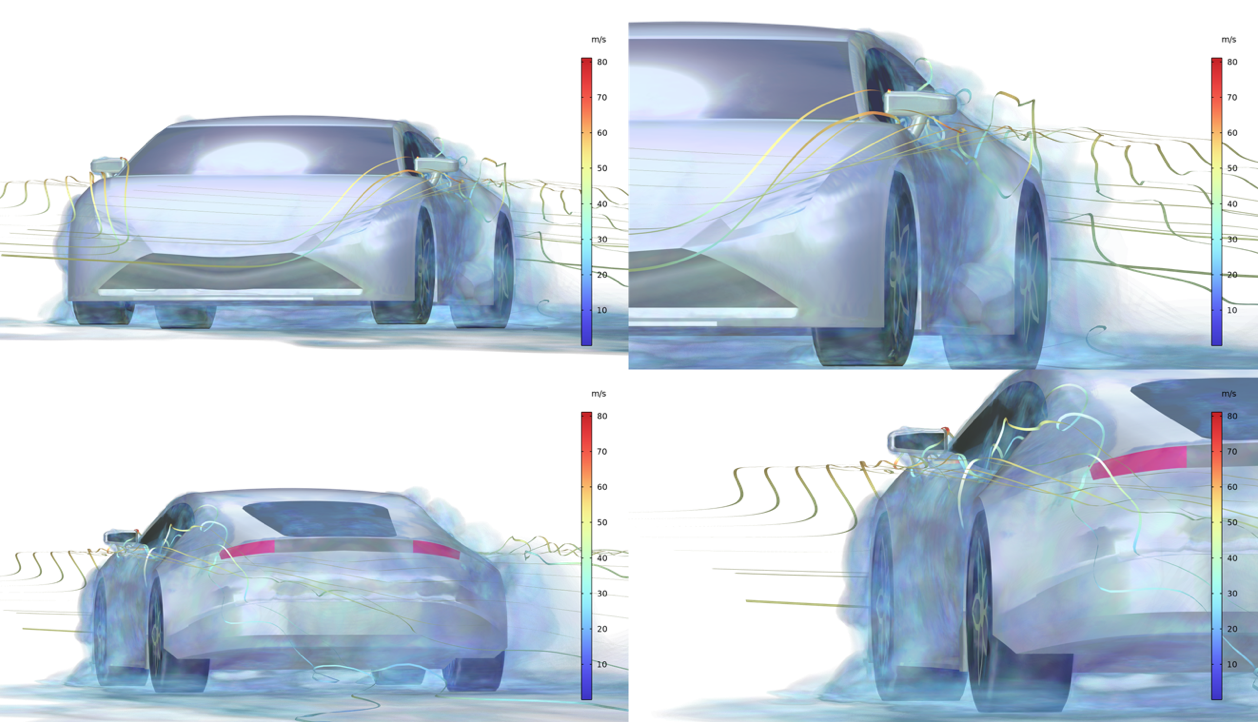
Das Strömungsfeld um das Auto und eine Vergrößerung nahe der Seitentüren.
Das Strukturmodell unter Verwendung einer einseitigen FSI-Studie
Wir können ein erstes Testbeispiel im Zeitbereich mit den von der Strömung ausgeübten Kräften durchführen. Dies gibt uns nicht nur ein Gefühl für die zu erwartenden Verformungen des Spiegels, sondern sollte auch zu einigen coolen Animationen führen. (Man sollte die Bedeutung von schönen Animationen nie unterschätzen!) Unten sehen wir, wie die Strömung den Spiegel verformt. Die Verformungen sind zur Veranschaulichung um den Faktor 50 übertrieben.
Schwingung des Spiegels durch die Strömung. Man beachte, dass die Verformung um den Faktor 50 übertrieben ist, sonst würde man die Bewegung des Spiegels nicht sehen.
Bei der Zeitbereichsanalyse wird jedoch davon ausgegangen, dass die Anfangsbedingungen gleich Null sind. Außerdem müsste eine gute Zeitbereichsanalyse aufgrund der Zufallsbelastung über einen sehr langen Simulationszeitraum durchgeführt werden, um zuverlässige Ergebnisse zu erzielen. Wir müssen also einen anspruchsvolleren Ansatz verwenden.
Der nächste Schritt besteht darin, ein Strukturmodell im Frequenzbereich zu definieren, um zu sehen, wie verschiedene Einzelteile der Tür schwingen können. Dazu verwenden wir zunächst die FFT, um die durch die Strömung verursachten schwankenden Kräfte aus dem Zeitbereich in den Frequenzbereich zu übertragen. In diesem Fall verwenden wir für die Strömungssimulation einen Zeitbereich von 0,7 s. Das letzte Intervall von 0,1 s, also von 0,6 bis 0,7, zeigt, dass die Strömung bereits stabil ist. Dies ist nach 35 m Fahrt mit 180 km/h der Fall, was 8 Autolängen entspricht. Da wir nun eine Periode von 0,1 s abtasten, beträgt die Auflösung im Frequenzbereich 10 Hz. Mit einem längeren Abtastintervall ließe sich die Frequenzauflösung erhöhen. Die Gesamtkraft im Seitenfenster zeigt Ausschläge bei 90 Hz und 160 Hz. Der Seitenspiegel hat einen starken Ausschlag bei 50 Hz und ein Plateau im Bereich von 70-90 Hz. Wenn die Spitzen in den Frequenzspektren mit wichtigen Eigenfrequenzen der Struktur zusammenfallen würden, besteht die Gefahr einer Verstärkung durch Resonanz.
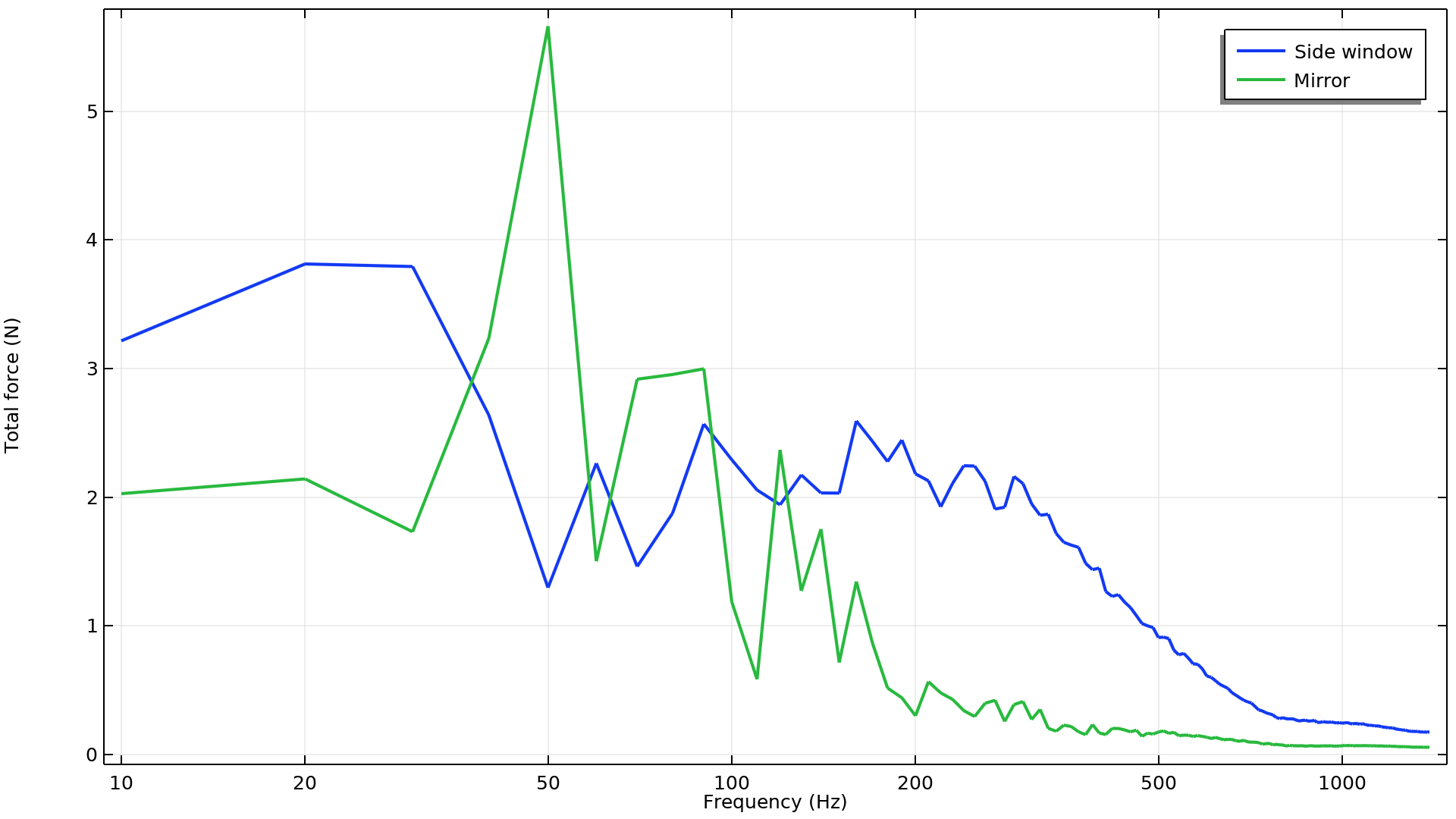
In diesem Diagramm sind die Gesamtkräfte auf das Seitenfenster und den Spiegel als Funktion der Frequenz dargestellt. Die statische Belastung durch die mittlere Strömung ist nicht enthalten.
Die folgende Abbildung zeigt den Modellbaum für die Übertragung der schwankenden Kräfte in den Frequenzbereich und für die Durchführung der Strukturanalyse zur Ermittlung der Antwort.
Modellbaum für die Strukturanalyse im Frequenzbereich. Studie 4 überträgt die Windlasten aus dem Zeitbereich in den Frequenzbereich. In Studie 5 wird die Frequenzbereichsstudie mit der Anregung durch die Windlast durchgeführt. Die Lösung wird dann im letzten Studienschritt zurück in den Zeitbereich übertragen.
Sobald wir die Spannungen im Fluid in den Frequenzbereich transformiert haben, können wir sie als Lasten auf die Tür und den Spiegel anwenden. Bei dieser Analyse können wir die gesamte Geometrie der Seitentür verwenden, müssen aber den Rest des Fahrzeugs nicht berücksichtigen. Eine interessante angeregte Mode bei 90 Hz ist unten dargestellt. Es ist zu erkennen, dass das Seitenfenster mit einem Knoten an den Kanten schwingt und der obere Teil der Tür über dem seitlichen Aufprallträger mit einem Knoten schwingt. Es könnte schwierig sein, eine solche Mode vollständig zu dämpfen. Das bedeutet, dass wir den Wind bei dieser Frequenz wahrscheinlich hören würden.
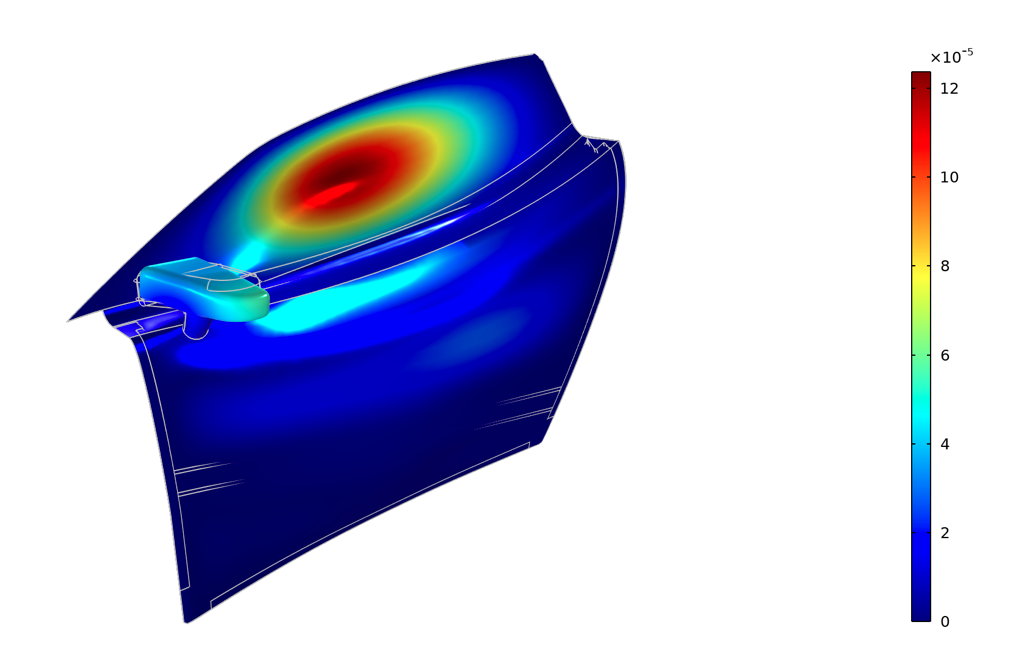
Die Reaktion auf die Fluidlast bei 90 Hz. Das gesamte Seitenfenster und die Seitentür schwingen fast gleichmäßig über einen großen Teil ihrer Flächen.
Eine weitere interessante Mode finden wir bei 50 Hz. Hier schwingen sowohl die Innenstruktur der Tür als auch der Seitenspiegel als Reaktion auf die Fluid-Lasten auf den Außenflächen. Wir können jedoch hoffen, dass die am Metall befestigte Verkleidung zur Dämpfung der Schwingungen an der Innenstruktur beitragen kann.
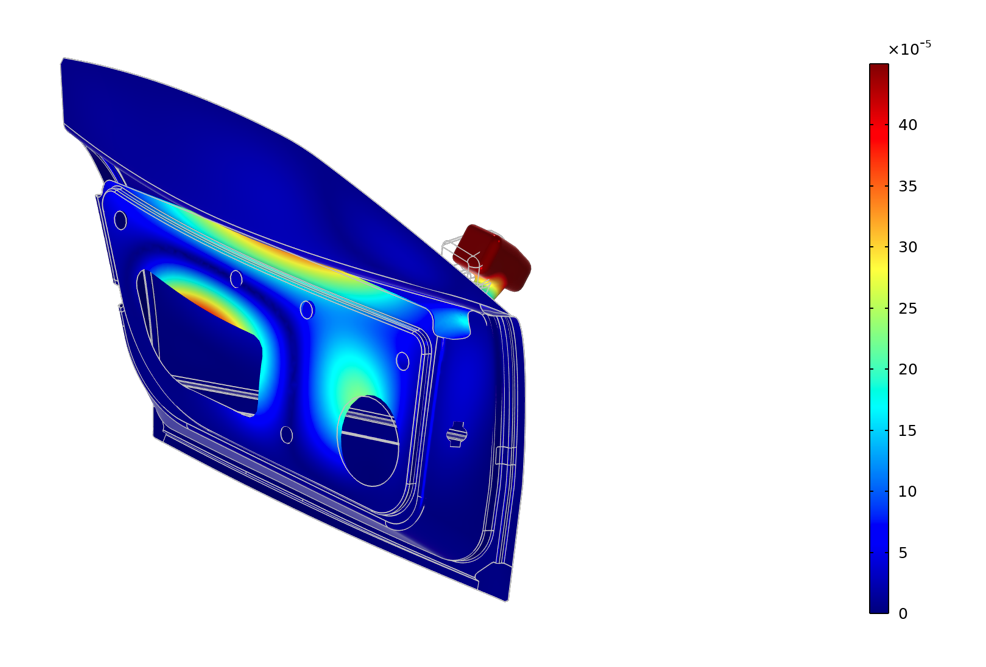
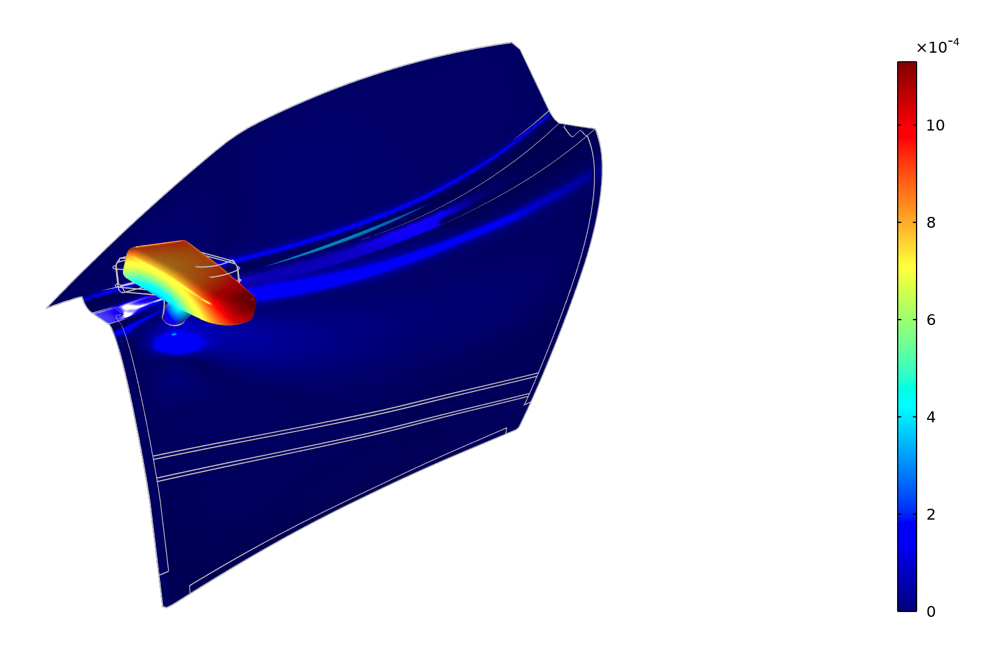
Die Antwort bei 50 Hz zeigt, dass sowohl die innere Metallstruktur der Seitentür als auch der Seitenspiegel vibrieren. Dies wird wahrscheinlich durch die an dieser Fläche angebrachte Verkleidung gedämpft.
Das schlimmste Flattergeräusch tritt auf, wenn Sie das Fenster ein wenig herunterkurbeln müssen, beispielsweise um etwas frische Luft ins Auto zu lassen. Dann ist die Oberkante des Fensters nicht eingespannt und die Eigenmoden zeigen, dass das gesamte Seitenfenster flattert. Die Schwingungen der oberen Kante der Fensterscheibe treten bei 20 Hz auf.

Die Antwort bei 20 Hz erzeugt Vibrationen der oberen hinteren Ecke des Seitenfensters.
Erweiterung des Modells der Windlast auf einen Sportwagen
Für die Karosserie gelten mehrere Vereinfachungen. So wird beispielsweise davon ausgegangen, dass die verschiedenen Teile der Karosserie perfekt zusammengebaut sind, also weder Lücken noch Ausrichtungsfehler zwischen verschiedenen Karosserieteilen bestehen. In Wirklichkeit ist das Gehäuse eines echten Supersportwagens voller kleiner Lücken zwischen den Karosserieteilen und den Türen in der Größenordnung von einem Millimeter. Diese Lücken können zu zusätzlichen Turbulenzen führen. Eine weitere Vereinfachung ist, dass sich die Räder im CFD-Modell nicht drehen. Dies dürfte ebenfalls zu Turbulenzen führen. Bei der Strukturanalyse wird davon ausgegangen, dass die Tür verlagerungsfrei an den Rahmen des Fahrzeugs gebunden ist. In Wirklichkeit schwingt auch der Fahrzeugrahmen, hauptsächlich aufgrund der Straßenunebenheiten, die sich über den Antriebsstrang und die Aufhängung des Fahrzeugs auf den Rahmen und dann auf die Türen ausbreiten.
Trotz der Vereinfachungen ist das Modell immer noch recht anspruchsvoll und kann sehr gut als Ausgangspunkt für ein genaueres Modell verwendet werden. Eine Erweiterung des Modells könnte die Windschutzscheibe und die Heckscheibe einbeziehen und eine vollständige Analyse der Schwingungen des Fensters, der Hauptquelle des Lärms, durchführen. Darüber hinaus könnten wir die anhand der FSI-Studie berechneten Schwingungen als Randbedingungen für eine Akustikstudie des Fahrzeuginnenraums verwenden. Dies würde eine detaillierte Geometrie der Kabine beinhalten, beispielsweise die Türverkleidungen, Sitze, Teppiche, Instrumentierung usw. Aber das ist ein Thema für einen anderen Blog-Beitrag!
Nächster Schritt
Möchten Sie eine LES-Studie eines Autospiegels und einer Autotür ausprobieren? Klicken Sie auf die Schaltfläche unten, dort finden Sie die Modelldatei.




Kommentare (0)