Markierte Blog-Beiträge Technische Inhalte
Verwendung von Jobsequenzen zum Speichern von Daten nach der Lösung Ihres Modells
Die Anleitung in diesem Blog-Beitrag richtet sich an alle, die nach der Lösung eines Modells häufige Aufgaben automatisieren möchten. Hier lernen Sie, Jobsequenzen zu verwenden.
So exportieren Sie Bilder automatisch nach der Lösung Ihres Modells
Wussten Sie, dass COMSOL Multiphysics® nach der Lösung Ihres Modells automatisch Ergebnisbilder und Animationen exportieren kann? Nähere Informationen finden Sie hier.
Importieren von Bildern und Lofting eines Festkörpers
Angenommen, Sie wollen eine unregelmäßige Form modellieren, zum Beispiel einen menschlichen Kopf. Hier zeigen wir, wie Sie durch das Importieren von Bildern und Lofting eines Festkörpers die Geometrie dazu einrichten können.
Methoden für die schnellere Modellierung von Bandpassfiltern
Entwerfen Sie hochwertige Geräte mit Bandpassfilter mithilfe der Finite-Elemente-Methode im Frequenzbereich? Hier finden Sie einige Methoden, mit denen Sie den Modellierungsprozess beschleunigen können.
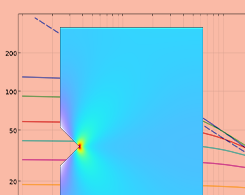
Wie werte ich singuläre Spannungsfelder aus?
Erfahren Sie mehr über die Eigenschaften singulärer Spannungsfelder und lernen Sie einige mögliche Ansätze zu deren Auswertung in COMSOL Multiphysics® kennen.
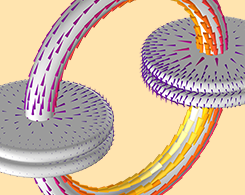
Was wir aus dem Kondensator-Paradoxon lernen können: Existieren Kapazität und Induktivität?
Was ist das Kondensator-Paradoxon? Wie kann es durch Modellierung und Simulation gelöst werden? Existieren Kapazität und Induktivität? Hier finden Sie Antworten.
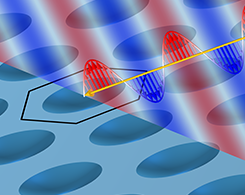
Beugung höherer Ordnung verstehen
Entdecken Sie, wie Sie die Ewald-Kugel verwenden können, um die Beugung an planaren periodischen Strukturen zu untersuchen. (Interagieren Sie direkt mit dem Modell, um ein vollständiges Bild zu erhalten!)
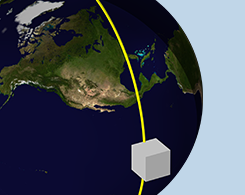
Berechnung der Wärmelasten im Orbit mit COMSOL Multiphysics®
Seit Version 6.1 verfügt das Heat Transfer Module über ein neues Interface zur Definition von Satellitenbahnen und -ausrichtungen, Bahnmanövern und unterschiedlichen Planeteneigenschaften.