Simulation von MEMS-Beschleunigungsmessern und -Gyroskopen zur Verwendung in inertialen Messeinheiten

In der heutigen Zeit beginnen die meisten Menschen eine Reise nicht ohne ein Navigationsgerät, das mit dem Global Positioning System (GPS) verbunden ist. GPS-Signale können jedoch unterbrochen werden, wenn ein Fahrzeug unterirdisch oder zwischen hohen Gebäuden fährt. Aus diesem Grund sind in vielen Fahrzeugen, Mobiltelefonen und anderen Geräten inertiale Messeinheiten (Inertial Measurement Units, IMUs) eingebaut. Eine inertiale Messeinheit verwendet unglaublich kleine und präzise Gyroskope und Beschleunigungsmesser, um die Bewegung im Verhältnis zu den orthogonalen x-, y-, und z-Achsen der Erde zu bestimmen. Die Komponenten einer inertialen Messeinheit, einschließlich der MEMS-Gyroskope und -Beschleunigungsmesser, können mit der Software COMSOL Multiphysics® modelliert werden.

You Are Here

Stellen Sie sich einen tiefschwarzen Himmel vor, dessen Dunkelheit durch Tausende von weißen Punkten erhellt wird, die in einer Form angeordnet sind, die sich als Milchstraße zu erkennen gibt, und über unserer Galaxie zeigt ein Pfeil mit dem wenig hilfreichen Text „YOU ARE HERE“ auf einen der kleinen Punkte.

Ein Beispiel für ein Navigationsinstrument mit einem wenig hilfreichen Referenzrahmen.

In diesem bekannten visuellen Witz finden sich einige Tatsachen über die relativistische Natur der Navigation (und des Lebens!) wieder. Die vielleicht wichtigste Erkenntnis ist, dass der Standort eines Objekts nur in Bezug auf den Raum, der es umgibt, sinnvoll beschrieben werden kann. In der Navigation ist dieser Raum der Referenzrahmen.

Wenn wir unseren Kurs auf einer Straßenkarte planen, navigieren wir innerhalb eines zweidimensionalen Referenzrahmens. Eine Karte allein kann uns nicht sagen, ob wir uns auf einem Hügel auf- oder abwärts bewegen oder ob unser Fahrzeug Gefahr läuft, sich zu überschlagen. Ein mit inertialen Messeinheiten ausgestattetes Navigationssystem kann die Bewegungsbahn eines Fahrzeugs im dreidimensionalen Raum berechnen, indem es sowohl die lineare als auch die Winkelbeschleunigung misst. Mit drei Beschleunigungssensoren, die jeweils entlang der x-, y-, und z-Achse ausgerichtet sind, können wir lineare Bewegungen im 3D-Raum verfolgen. Ebenso können wir mit drei Gyroskopen, die jeweils entlang der x-, y-, und z-Achse ausgerichtet sind, die Rotation im 3D-Raum messen. (Ref. 1)

Steine im Kopf? Bestandteil unserer Beschleunigungsmesser!

Wenn unsere Füße mal auf Stolpersteine stoßen, kann unser Kopf mit seinen Anti-Stolper-Steinen dagegensteuern. Der Körper jedes Wirbeltiers enthält mikroskopisch kleine Otolithen, die hauptsächlich aus Kalziumkarbonat bestehen – dem Hauptbestandteil von Kalkstein. (Otolith ist griechisch für „Ohrstein“.) Diese Steine in unseren Köpfen sind ein wesentlicher Bestandteil der natürlichen Beschleunigungsmesser unseres Körpers. (Ref. 2)

Ein Beschleunigungssensor besteht aus einer an einer flexiblen Struktur aufgehängten Testmasse, die an einem Gehäuse befestigt ist. Wenn das Gehäuse beschleunigt wird, wird auch die Testmasse beschleunigt, was zu einer messbaren Dehnung der Aufhängung führt. Bei den Beschleunigungssensoren in unseren Ohren besteht die Testmasse aus einem Bündel von Otolithen. Dieses Bündel ist an einer Membran befestigt, die an mikroskopisch kleinen Härchen und daran befindlichen Nerven hängt, welche bei einer Verschiebung der Masse elektrische Veränderungen wahrnehmen. Dieser organische Beschleunigungsmesser ist an unserer Innenohrstruktur befestigt, die als Referenzrahmen dient.

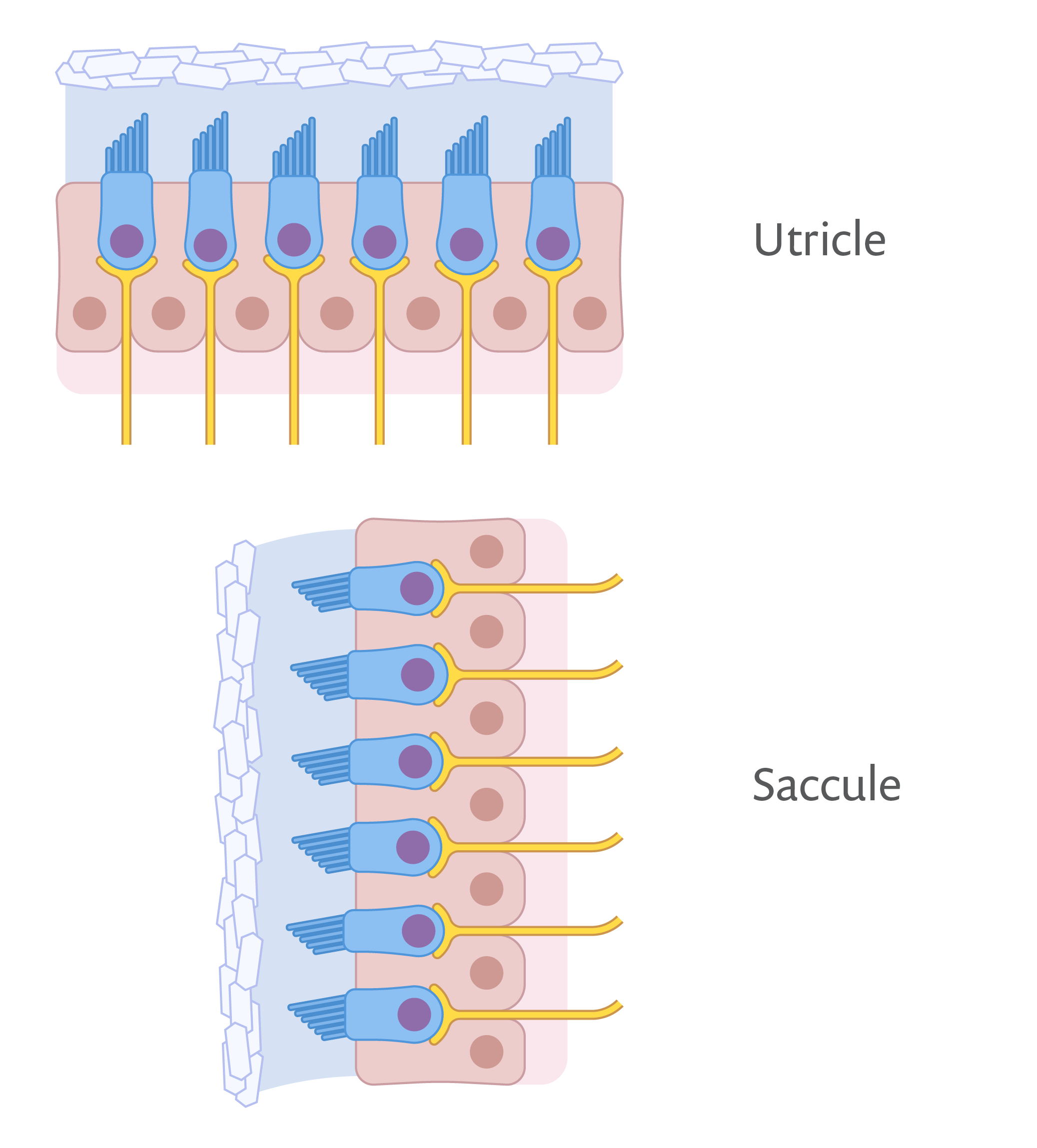
Der menschliche Körper enthält in jedem Ohr einen horizontal positionierten Utriculus und einen vertikalen Sacculus. Jede dieser mikroskopischen Strukturen enthält eine aufgehängte Testmasse, die als Antwort auf eine Beschleunigung die anschließenden Nerven stimuliert. (Ref. 3)

Wenn sich unser Körper abrupt bewegt, warnt die Verlagerung der Testmasse unsere Nerven vor einem möglichen Sturz. Unsere Nerven können dadurch Bewegungen in unserem Körper erkennen, selbst wenn andere Sinnesorgane wie unsere Augen oder Ohren ihre Referenzrahmen verlieren. Der oberflächenmikrobearbeitete Beschleunigungsmesser erfüllt eine ähnliche Funktion für Geräte und Fahrzeuge.

„Bausteine“ für die Modellierung eines MEMS-Beschleunigungssensors

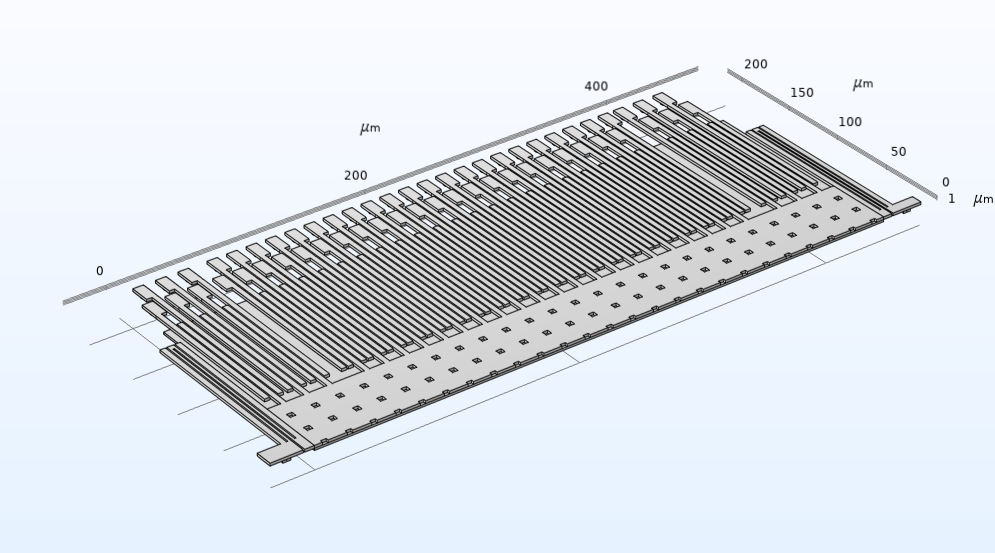
Das hier vorgestellte Tutorial-Modell zeigt, wie mithilfe des Multiphysik-Interfaces Electromechanics des MEMS Module ein oberflächenmikrobearbeiteter Beschleunigungssensor modelliert wird. Das Modell besteht aus drei Unterbaugruppen: der Testmasse, den verankerten Federn, die die Testmasse tragen, und der Elektrodenanordnung. In der Diashow werden alle drei Unterbaugruppen sowie das vollständige Modell gezeigt.

Wenn das Gerät einer Beschleunigung ausgesetzt ist, wird die Testmasse verschoben, wodurch sich die Kapazität zwischen den festen und den beweglichen Elektroden ändert. Diese Kapazitätsänderung ist proportional zur Beschleunigung.

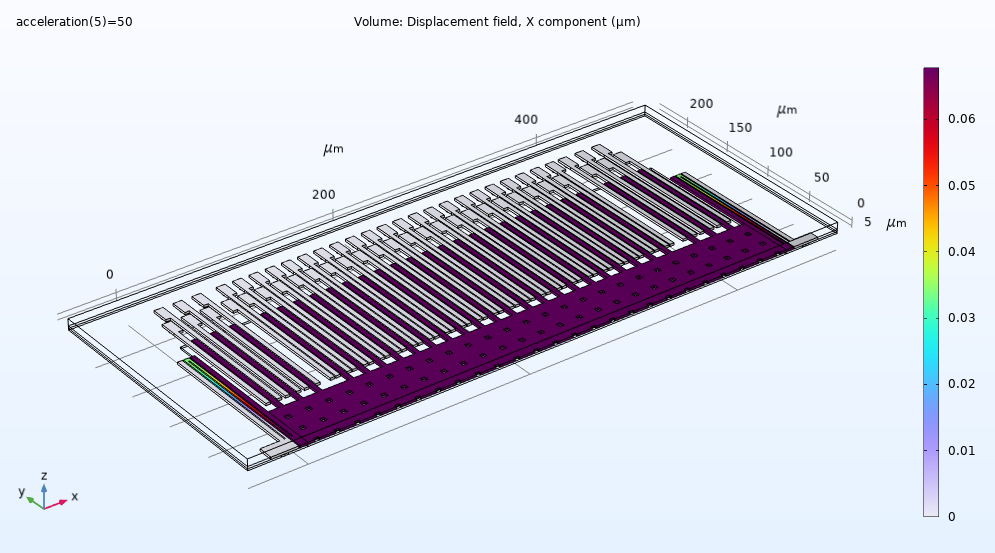
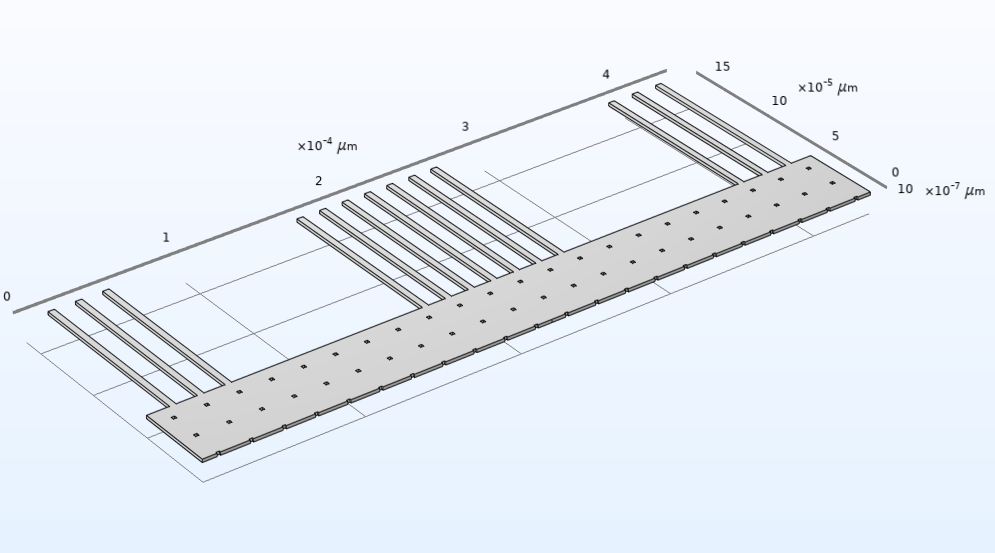
Verschiebung bei einer Beschleunigung von 50 g. In diesem Szenario bewegt sich die Testmasse um etwa 0,07 Mikrometer.

Bei der Definition des Modells können Sie Abmessungen, Ausrichtung und andere Attribute für die drei Kernmodule Testmasse, Federn und Elektroden festlegen. Sie können verschiedene Designoptionen ausprobieren, indem Sie die Werte der Schlüsselattribute für diese modularen Bausteine, auch Teilsequenzen genannt, anpassen. Diese Modularität unterstützt das simulierte Prototyping und Testen der Beschleunigungsmesserkomponenten und ihrer Konfiguration.

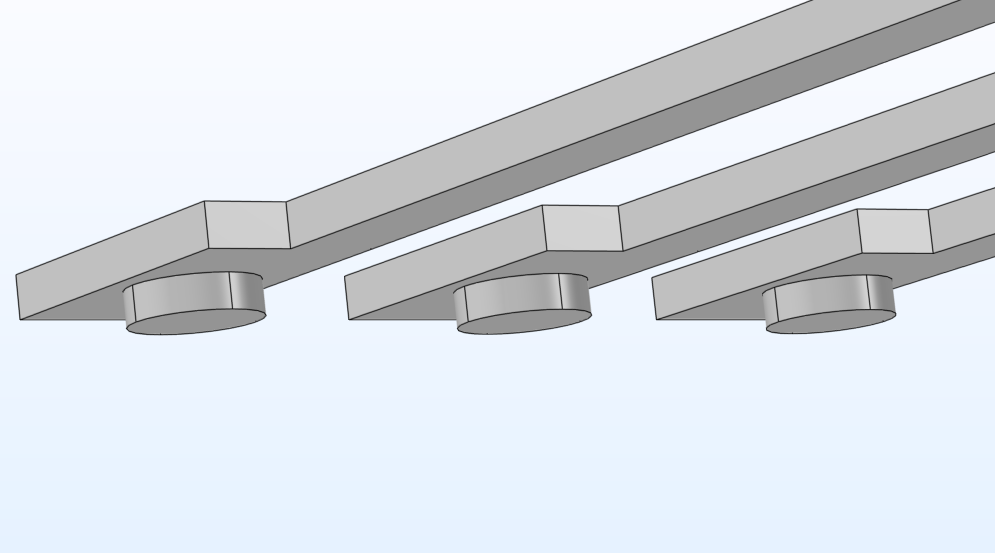
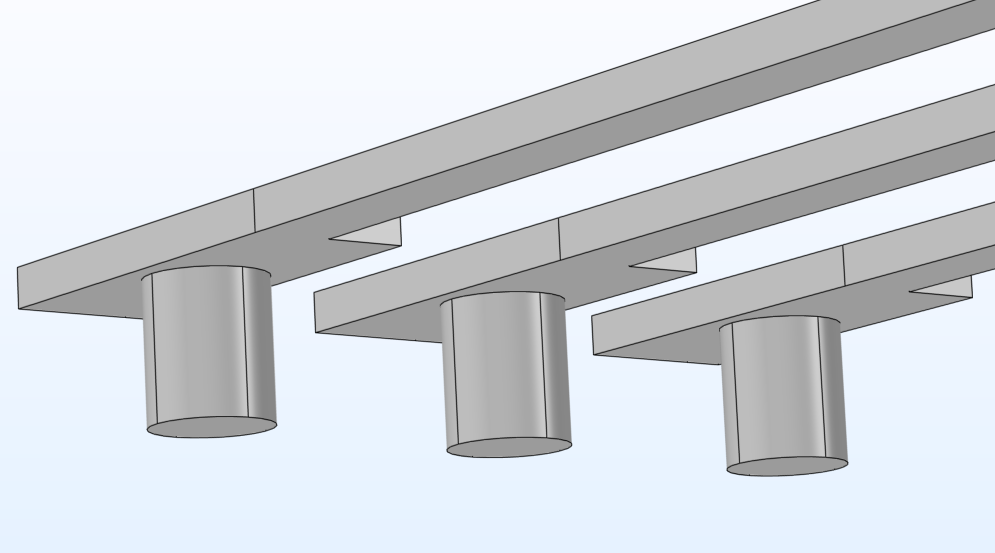
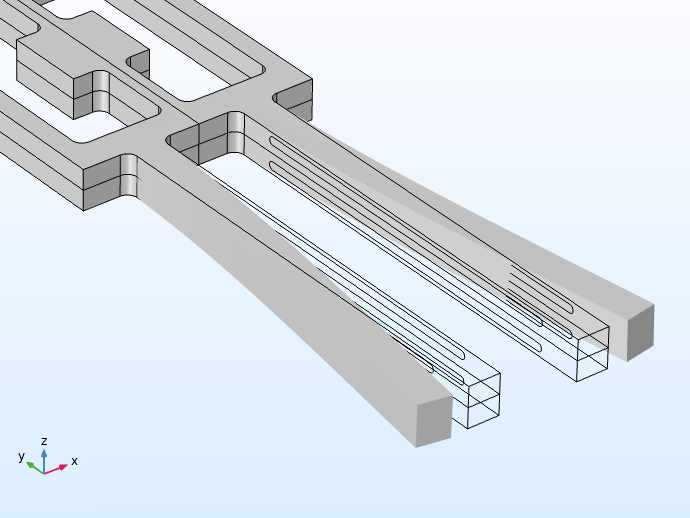
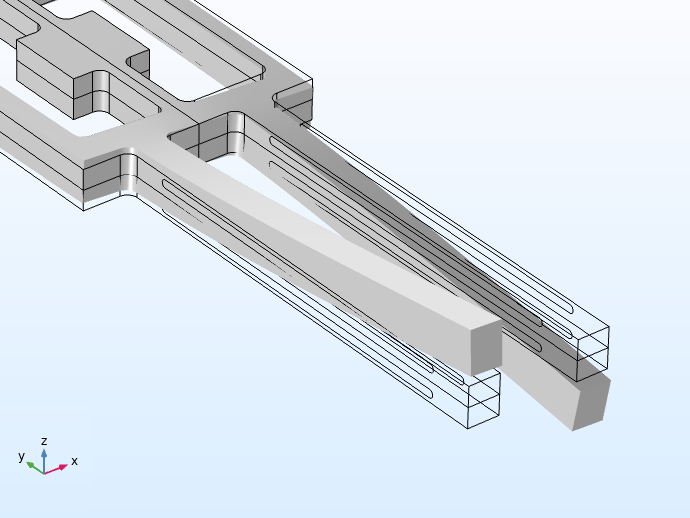
Links ist eine modulare Elektrodenanordnung für das Beschleunigungssensormodell zu sehen. Die überarbeitete Anordnung rechts wurde durch Anpassung der Schlüsselattribute aus derselben modularen Teilsequenz erstellt.

Die Höhen und Tiefen von Stimmgabel-Gyroskopen

Genauso wie die Natur einige Tiere mit Beschleunigungssensoren ausgestattet hat, tragen andere ihre eigenen Gyroskope! Stubenfliegen, Mücken und einige andere fliegende Insekten haben zwei Gliedmaßen, die Halteren genannt werden und die hinter den Flügeln dieser Schnake zu sehen sind:

Eine Aufnahme einer Schnake, die die Position ihrer Halteren zeigt. Originalbild von Andre Vrijens, lizenziert unter CC BY 3.0 über Wikimedia Commons.

Die Halteren eines Insekts schlagen zusammen mit seinen Flügeln. Im Horizontalflug beschreibt diese Bewegung eine Auf- und Ab-Kurve. Wenn das Insekt jedoch seinen Körper neigt, verschiebt sich die Flugbahn der Halteren aufgrund des Corioliseffekts. Dadurch bewegen sich die Halteren sowohl nach rechts und links als auch nach oben und unten. Das Insekt nimmt die Schwenkbewegungen der Halteren über den Druck wahr, den sie auf die mit ihnen verbundenen Haare ausüben. So kann es seine Ausrichtung in Bezug auf seine Flugbahn steuern.

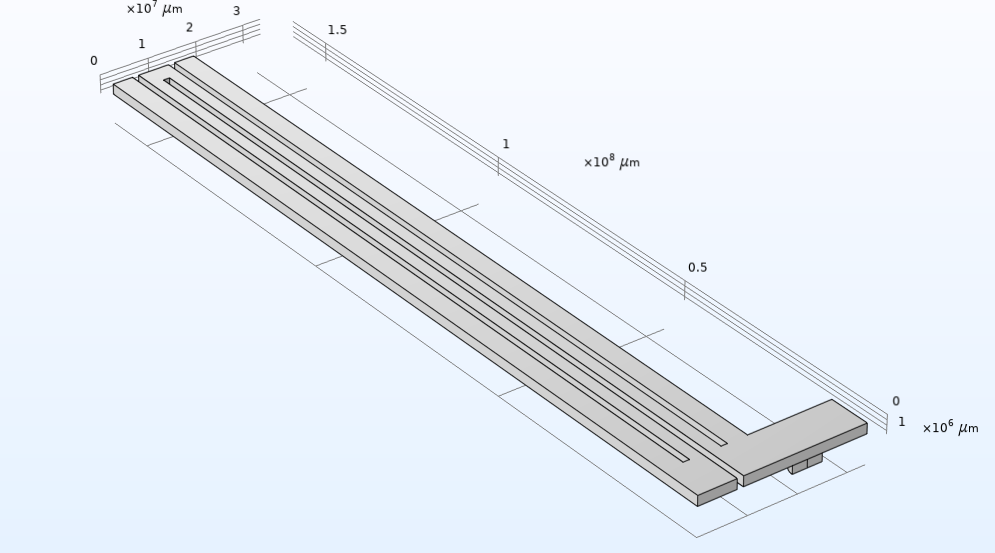
Ein piezoelektrischer Drehratensensor funktioniert nach einem ähnlichen Prinzip. Anhand eines Modells können wir uns ansehen, wie das funktioniert.

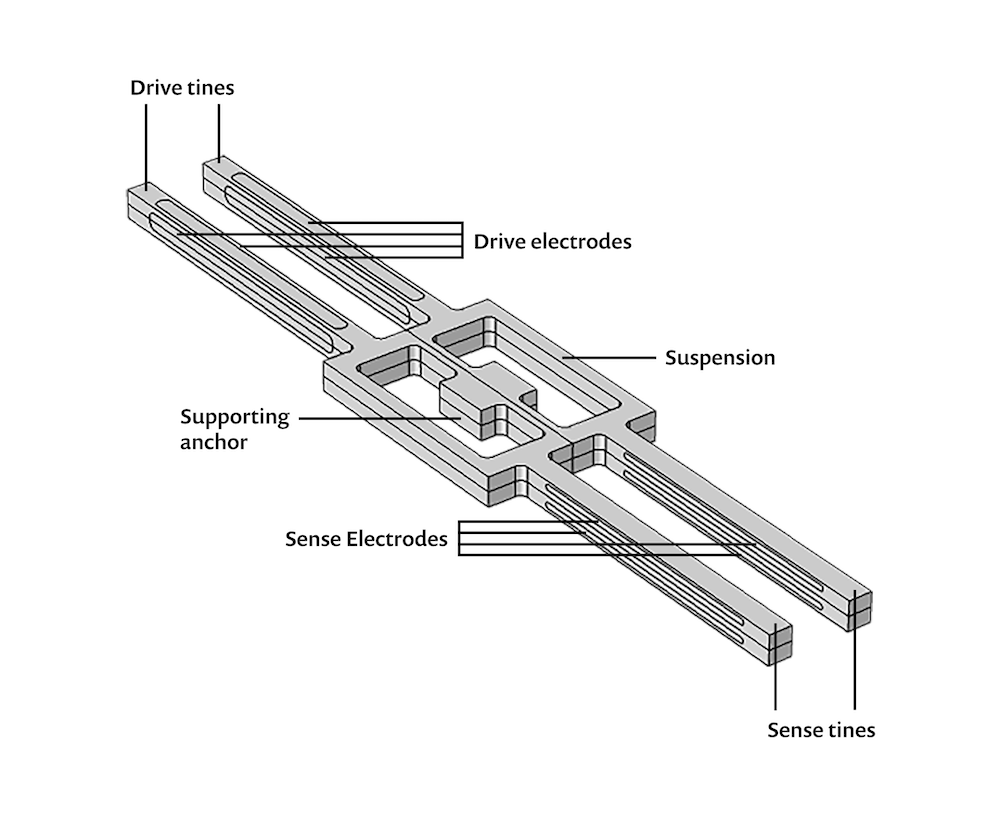
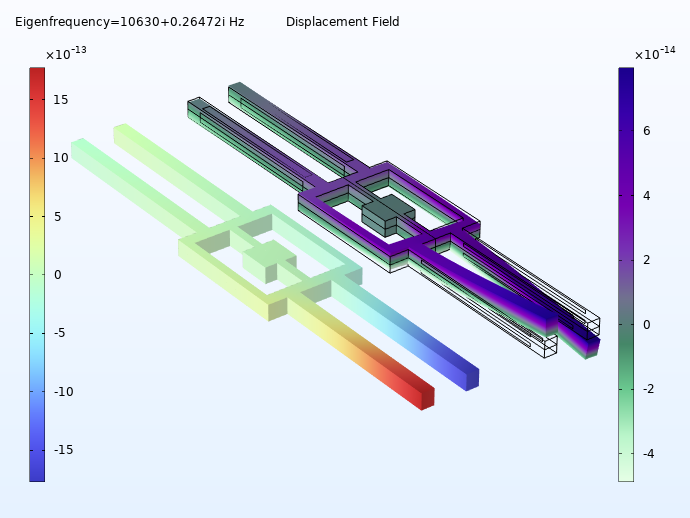
Ein Schema des modellierten Stimmgabel-Gyroskops, das die Symmetrieebene durch die Mitte des Geräts und die wichtigsten Komponenten zeigt.

Die rechteckige Form in der Mitte des Gyroskops ist seine Aufhängung. Der Stützanker dieses Elements ist fest mit dem Gerät verbunden, in den das Gyroskop eingebaut ist. Die beiden hervorstehenden Elementpaare sind die Antriebszinken und die Sensorzinken. Elektroden an beiden Zinkenpaaren ermöglichen die Bereitstellung nützlicher Daten über die Ausrichtung des Geräts.

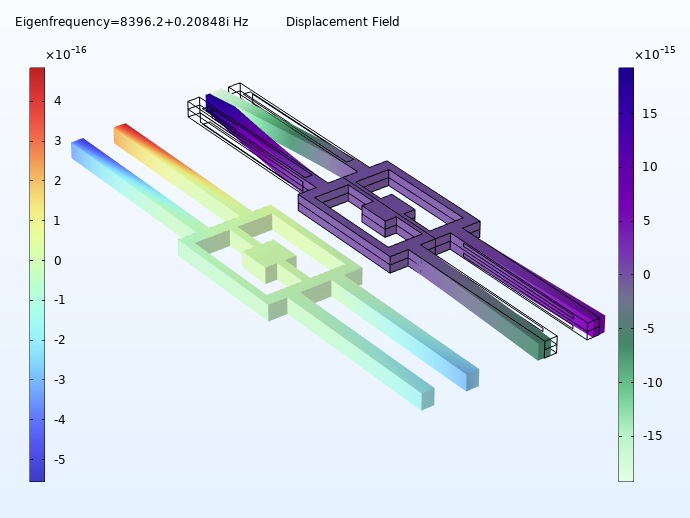
Um die Funktionsweise zu erklären, betrachten wir das Verhalten der Zinken, wenn sich das Gerät in Bezug auf seinen Referenzrahmen entweder im Stillstand befindet oder gleichförmig bewegt (Bewegung ohne lineare oder rotierende Beschleunigung). Anschließend betrachten wir das veränderte Verhalten der Zinken, wenn sich das Gerät dreht. Ein elektrisches Signal, das an die Antriebszinken angelegt wird, bewirkt die Vibration der Sensorzinken mit ihrer Resonanzfrequenz in der xy-Ebene. Wenn sich das Gerät um die y-Achse dreht, führt die Corioliskraft zu einer Vibration außerhalb der Ebene:

Links: Durch das Anlegen von Strom, während sich das Gerät in gleichförmiger Bewegung befindet, werden die Zinken entlang der xy-Ebene in Schwingung versetzt. Rechts: Durch die Drehung des Geräts um die y-Achse werden Schwingungen außerhalb der Ebene entlang der z-Achse erzeugt.

Die Antriebszinken und die Sensorzinken haben unterschiedliche Resonanzfrequenzen. Wenn das Gyroskop in Betrieb ist, regen Elektroden in den Antriebszinken diese über den inversen piezoelektrischen Effekt zu Schwingungen mit ihrer Resonanzfrequenz an. Wenn sich das gesamte Gerät um die y-Achse dreht, regt die resultierende Corioliskraft die Sensorzinken zu Schwingungen außerhalb der Ebene an, und diese Bewegung erzeugt über den direkten piezoelektrischen Effekt Strom in den Elektroden der Sensorzinken.

Das linke Bild zeigt zwei Plots des Geräts in gleichförmiger Bewegung, also ohne Beschleunigung oder Rotation. Die Zinken vibrieren innerhalb der xy-Ebene. Auf der rechten Seite rotiert das Gerät um die y-Achse, wodurch die Zinken aus der xy-Ebene heraus vibrieren. In beiden Bildern zeigt der Plot auf der linken Seite Farbvariationen, um die Größe der Verschiebung anzuzeigen, während der rechte Plot die tatsächliche Verschiebung der Zinken im Raum zeigt.

Eine Animation des Zinkenverhaltens, wenn sich das Gerät um die y-Achse dreht und dadurch Vibrationen außerhalb der Ebene verursacht. Links zeigt die Farbvariation die Größe der Verschiebung an, während rechts die Bewegung im Raum zu sehen ist.

Abschluss (und Fortsetzung)

Vielen Dank, dass Sie bis zum Ende dieses Beitrags gelesen haben! Über die folgenden Links können Sie mehr über die Modellierung von MEMS-Beschleunigungsmessern und -Gyroskopen erfahren:

• Schnell zum Beschleunigungsmesser-Modell: Surface Micromachined Accelerometer
• Eine Runde drehen mit dem Gyroskop-Modell: Piezoelectric Rate Gyroscope

Mehr über die Modellierung piezoelektrischer Bauelemente

• Modeling Piezoelectricity: Which Module to Use?
• How to Model Piezoelectric Devices as Both Transmitters and Receivers
• Simulating a MEMS-Based Pressure Sensor Inspired by a Cave Fish

Referenzen

1. B. Schweber, “The Autonomous Car: A Diverse Array of Sensors Drives Navigation, Driving, and Performance”, https://www.mouser.com/applications/autonomous-car-sensors-drive-performance/
2. D. Purves, G.J. Augustine, D. Fitzpatrick, et al., editors, “The Otolith Organs: The Utricle and Sacculus”, Neuroscience. 2nd edition. Sunderland (MA), Sinauer Associates, 2001; https://www.ncbi.nlm.nih.gov/books/NBK10792/
3. T. C. Hain, “Otoliths”, Mar. 2021; https://dizziness-and-balance.com/disorders/bppv/otoliths.html