Heutzutage ist die Raumakustiksimulation ein wesentlicher Bestandteil der Klanggestaltung, etwa bei der Erzeugung einer immersiven virtuellen Szene, der Entwicklung einer angenehmen akustischen Umgebung in einem Raum oder der Optimierung eines Klangerlebnisses. Das Acoustics Module, ein Add-On zur Software COMSOL Multiphysics®, bietet mehrere Interfaces, die sich gut für die Raumakustiksimulation eignen. In diesem Blog-Beitrag geht es um die Bedeutung schallabsorbierender Randbedingungen für die Raumakustikmodellierung.
Schallabsorptionsleistung
Um die schallabsorbierende Randbedingung zu verstehen, werden wir uns zunächst mit dem Schallabsorptionskoeffizienten befassen. Die folgenden drei Größen werden verwendet, um die Absorptionseigenschaften von Absorbern auszudrücken (Ref. 1):
- Schallabsorptionskoeffizient, \alpha: das Verhältnis von nicht reflektierter Schallenergie zu einfallender Schallenergie
- Spezifische akustische Impedanz, Z_{\rm n}: das Verhältnis von Schalldruck zur normalen Teilchengeschwindigkeit auf der Oberfläche des Schallabsorbers
- Komplexer Druckreflexionskoeffizient, R: das Verhältnis des reflektierten Schalldrucks zum einfallenden Druck
Wir analysieren diese Parameter nun anhand der idealen Situation, dass eine ebene Welle in den porösen Absorber eintritt.
Ebene Welle, die in poröses Material einfällt.
Hier werden die Wellenzahlen für Luft und poröses Material als jeweils k und k_{\rm e} angenommen. Der Schalldruck für Einfall, Reflektion und Übertragung ist jeweils p_{\rm i}, p_{\rm r} und p_{\rm t}. Die Winkel für Einfall, Reflektion und Übertragung sind \theta, \psi und \phi. Die Amplituden von einfallendem und reflektiertem Schall werden durch A_{\rm i} und A_{\rm r} dargestellt und B_{\rm t} und B_{\rm b} stehen für die wandernden und rückwärtigen Klänge in porösen Medien. Der poröse Absorber mit einer Dicke von d m wurde als äquivalentes Fluid angenommen (besuchen Sie unsere Multiphysics Cyclopedia für weitere Informationen). Die Terminierung mit starrem Rand wurde auf x=d festgelegt.
Aus der linearen akustischen Wellengleichung lässt sich die Partikelgeschwindigkeit in x-Richtung der einfallenden, reflektierten und übertragenen Klänge, die jeweils v_{\rm i}, v_{\rm r} und v_{\rm t} sind, ausdrücken als:
Hierbei bezeichnen Z_{\rm 0} und Z_{\rm C} die charakteristische Impedanz der Luft und des porösen Materials. Aus der Definition ergibt sich der Reflexionskoeffizient wie folgt:
Für den Rand der Schnittstelle zwischen Luft- und poröser Schicht (x=0) gelten die folgenden zwei kontinuierlichen Bedingungen:
Mit diesen kontinuierlichen Bedingungen und dem Fermatschen Prinzip, \theta=\phi, kann die spezifische akustische Impedanz ausgedrückt werden als:
Also:
Der Absorptionskoeffizient kann mit der folgenden Gleichung bestimmt werden.
Somit kann die Schallabsorption an Rändern modelliert werden, indem den Rändern eine von drei Größen zugewiesen wird. Die obige Gleichung zeigt auch, dass \alpha von Natur aus abhängig vom Einfallswinkel ist. R und Z_{\rm n} sind komplexe Parameter mit Phaseninformationen, während \alpha ein Energieparameter ist. Die Phaseninformationen sind wichtig für die genaue Simulation der Raummoden. Daher sind die komplexen Parameter im Allgemeinen bessere Eingaben für wellenbasierte Raumakustiksimulationen. Andererseits ist der Schallabsorptionskoeffizient die Hauptausgabe im Schallabsorptionstest und gut zur intuitiven Ablesung der Absorberleistung geeignet. Der Absorptionskoeffizient bei zufälligem Einfall, der den über Raumwinkel gemittelten Wert darstellt, wird als praktische Leistung von Absorbern verwendet.
In den folgenden Gleichungen untersuchen wir die akustische Impedanz des porösen Materials weiter.
Der Transmissionsdruck und die Geschwindigkeit bei x=0 sind:
Dagegen sind sie bei x=d:
Mit diesen Gleichungen können wir die Parameter am Einlass mit Endwerten in der folgenden Matrixform ausdrücken:
p_{\rm t}(0) \\
v_{\rm t}(0) \\
\end{bmatrix}=\begin{bmatrix}
\cos{(k_{\rm e}d\cos\phi)} & j\frac{Z_{\rm C}}{\cos\phi}sin{(k_{\rm e}d\cos\phi)} \\
j\frac{\cos\phi}{Z_{\rm C}}sin{(k_{\rm e}d\cos\phi)} & \cos{(k_{\rm e}d\cos\phi) \\
\end{bmatrix}
\begin{bmatrix}
p_{\rm t}(d) \\
v_{\rm t}(d) \\
\end{bmatrix}={\bm T}_{\rm F}\begin{bmatrix}
p_{\rm t}(d) \\
v_{\rm t}(d) \\
\end{bmatrix}
Hierbei ist {\bm T}_{\rm F} die Transfermatrix der Fluidschicht, die häufig für die Modellierung der Schallabsorption und -dämmung mithilfe der Transfermatrixmethode (TMM) verwendet wird (Ref. 2). Mit dem Snellius-Gesetz ksin\theta = k_{\rm e}\sin\phi können wir {\bm T}_{\rm F} mithilfe der folgenden Formel umschreiben:
\cos{(k_{\rm n}d)} & jZ_{\rm C}\frac{k_{\rm e}}{k_{\rm n}}sin{(k_{\rm n}d)} \\
j\frac{1}{Z_{\rm C}}\frac{k_{\rm n}}{k_{\rm e}}sin{(k_{\rm n}d)} & \cos{(k_{\rm n}d) \\
\end{bmatrix}
Hierbei ist k_{\rm n}=(k_{\rm e}^2-k^2\sin^2{\theta})^{\frac{1}{2}}. Unter der starren Randbedingung am Terminal (v_{\rm t}(d) = 0) können wir die spezifische akustische Impedanz des porösen Absorbers wie folgt berechnen:
Die obige Gleichung zeigt, dass die spezifische akustische Impedanz selbst winkelabhängig ist. Um die Schallabsorption an einem Rand vollständig zu modellieren, sollte daher die Winkelabhängigkeit der Absorberimpedanz berücksichtigt werden.
Lokale und erweiterte Reaktionsmodelle
Bei der Modellierung der Schallabsorption an Rändern werden zwei Arten von Absorptionsrandmodellen verwendet: lokale und erweiterte Reaktionsmodelle. Das lokale Reaktionsmodell, ein Standard in der Raumakustiksimulation, verwendet die winkelunabhängige Impedanz (im Allgemeinen unter Verwendung des Impedanzwerts der normalen Einfallsbedingung), um die Schallabsorptionseigenschaft des Randes zu beschreiben. Die Partikelgeschwindigkeit an einem bestimmten Punkt auf der Oberfläche des Absorbers wird als unabhängig vom Verhalten an anderen Punkten auf der Oberfläche angenommen. Das erweiterte Reaktionsmodell passt die winkelabhängige Impedanz an. Das lokale Reaktionsmodell ist zwar nur eine Annäherung, aber es ist effizient und eignet sich gut für die Modellierung von Schallabsorbern, deren akustische Impedanz nur wenig winkelabhängig ist, wie bei porösen Materialien mit starrer Rückseite und hohem Strömungswiderstand und bei Absorbern mit Wabenkern. Das erweiterte Reaktionsmodell ist genau, erfordert jedoch generell eine zusätzliche Modellierung des Absorberinneren. Für eine genaue und effiziente Raumakustikmodellierung sollte ein geeignetes Absorptionsrandmodell für den in Räumen installierten Absorber gewählt werden. Im Folgenden wird die Auswirkung des Absorptionsrandtyps auf den Absorptionskoeffizienten bei zufälligem Einfall sowohl theoretisch als auch numerisch gezeigt.
Auswirkungen verschiedener Oberflächenmodelle auf die Absorptionsleistung
Die Absorptionsleistung des porösen Absorbers mit starrer Rückseite und des Akustikvorhangs mit einer dahinterliegenden Luftschicht wurde bewertet. Das poröse Material wurde als äquivalentes Fluid mit einer Dicke von 100 mm angenommen. Die Fluideigenschaft wurde mithilfe des empirischen Miki-Modells mit einem Strömungswiderstand von 13.900 Pa s/m2 modelliert. Da der verwendete Akustikvorhang im Verhältnis zur Wellenlänge bei den untersuchten Frequenzen sehr dünn ist, wurde das permeable Membranmodell verwendet und dann mit der Luftschicht gekoppelt. Mit diesem Modell wurde die Transferimpedanz des Vorhangs anhand der folgenden Gleichung berechnet:
Hierbei stellen R_{\rm C} und M_{\rm C} jeweils den Strömungswiderstand und die Oberflächendichte dar, die auf 416 Pa s/m und 0,5 kg/m2 eingestellt wurden. Für die theoretische Studie wurde die TMM verwendet und der statistische Absorptionskoeffizient als zufälliger Inzidenzwert ausgewertet. Die Definition des statistischen Absorptionskoeffizienten \alpha_{\rm s} lautet:
Die Transfermatrix von dünnem Material {\bm T}_{\rm T} wird ausgedrückt als:
1 & Z_{\rm t} \\
0 & 1 \\
\end{bmatrix}
Mit dieser Transfermatrix ergibt die spezifische akustische Impedanz des akustischen Vorhangs mit Luftschicht folgendes:
Für die TMM kann das lokale Reaktionsmodell durch Substitution von \theta=0 bewertet werden.
Bei der numerischen Untersuchung berechnen wir den Hallraum-Absorptionskoeffizienten, also den im Hallraum gemessenen Absorptionskoeffizienten. Der Wert des Koeffizienten hängt vom gemessenen Raum und der Stichprobengröße ab. Der Absorptionskoeffizient wurde bereits in der ISO:354 als Messverfahren standardisiert und wird häufig beim konkreten raumakustischen Design eingesetzt.
Zur effizienten Simulation der Messung des Hallraum-Absorptionskoeffizienten mit COMSOL Multiphysics® wurde der einzige harte Boden mit integriertem Schallabsorber in zwei Dimensionen modelliert:
Eingebettetes Schallabsorbermodell zur Bewertung des Absorptionskoeffizienten des Hallraums.
Die Verifizierungsstudie in Ref. 3 hat gezeigt, dass dieses vereinfachte Modell der Messung des Hallkoeffizienten sehr nahe kommt.
Das Interface Pressure Acoustics, Boundary Elements wurde zur Modellierung des einfallenden Druckfeldes und des starren Bodens verwendet, und das Interface Pressure Acoustics, Frequency Domain wurde zur Modellierung des Drucks im Absorber verwendet. Das Feature Poroacoustics wurde für das poröse Material verwendet. Mit dem Feature Acoustic FEM–BEM Boundary kann die Transferimpedanz des akustischen Vorhangs gleichzeitig eingestellt werden. Für die lokale Reaktionsmodellierung wird das Gebiet des Absorbers deaktiviert und die entsprechende normale einfallende akustische Impedanz wird der Oberfläche des Absorbers zugewiesen. Die Bewertung des Hallraum-Absorptionskoeffizienten erfolgt in den folgenden Schritten:
- Bewertung der einfallenden W_{{\rm i},\theta_n} und der absorbierten Energie W_{{\rm a},\theta_n} auf der Absorberoberfläche für eine ebene Welle mit einem Einfallswinkel von \theta_n.
- Berechnung des Verhältnisses der gesamten absorbierten Energie zur gesamten einfallenden Energie mit der nachfolgenden Gleichung.
Der Hallraum-Absorptionskoeffizient \alpha_{\rm r} lautet folgendermaßen:
Hierbei ist N die Anzahl der Einfallswinkel. Im numerischen Test wurde das einfallende Feld der ebenen Welle mit Background Pressure Field modelliert, und W_{{\rm i},\theta_n} und W_{{\rm a},\theta_n} wurden wie folgt definiert:
wobei p_0 eine Amplitude des einfallenden Drucks und \bm n und {\bm I}_{\theta_n} jeweils der Normalvektor und der Schallintensitätsvektor des Einfallswinkels {\theta_n} auf der Absorberoberfläche sind.
Die folgende Grafik vergleicht die Absorptionskoeffizienten des porösen Absorbers bei zufälligem Einfall. Der Unterschied zwischen den lokalen und den erweiterten Reaktionen ist gering, aber insbesondere bei hohen Frequenzen erkennbar. Daher scheint das lokale Reaktionsmodell, wie bereits erwähnt, eine gute Annäherung für das poröse Material mit dem hohen Strömungswiderstand und dem starren Ende zu sein.
Die Absorptionskoeffizienten des porösen Absorbers bei zufälligem Einfall.
Andererseits zeigt der Vergleich der Absorptionskoeffizienten des Akustikvorhangs bei zufälligem Einfall, wie nachfolgend dargestellt, die große Diskrepanz zwischen dem lokalen und dem erweiterten Reaktionsmodell. Dies ist auf die starke Abhängigkeit der Luftschicht vom Einfallswinkel zurückzuführen. Außerdem entspricht dies der Regel, dass die erweiterte Reaktionsmodellierung für Absorber mit Luftschicht wichtig ist.
Die Absorptionskoeffizienten des Akustikvorhangs bei zufälligem Einfall.
Hallraum-Absorptionskoeffizienten vs. statistische Werte?
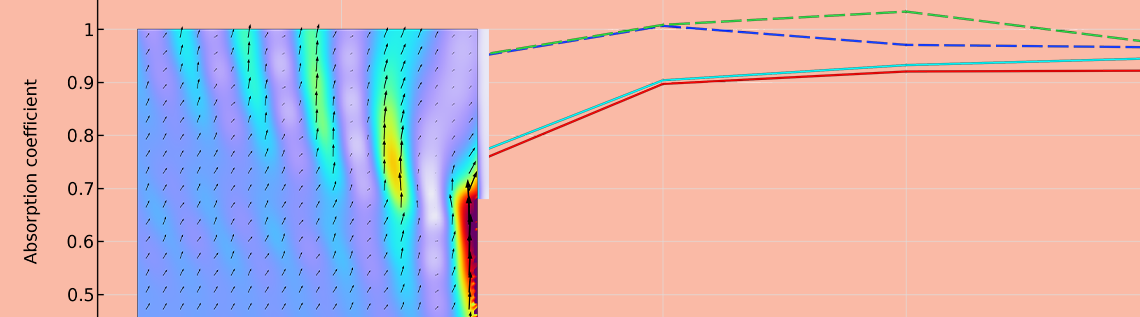
Wie in den vorherigen Diagrammen zum Absorptionskoeffizienten zu sehen ist, liegen die Absorptionskoeffizienten des Hallraums unabhängig von der Art der Absorber und der Absorptionsrandmodelle über den statistischen Werten und über 1 (über der perfekten Absorption). Dieses Phänomen, das als „Randeffekt“ bezeichnet wird, ist typisch für reale Messungen und wird durch den Energiefluss vom starren Boden zur Absorberoberfläche verursacht. Eine solche Situation wird nachfolgend gegenüber dem erweiterten Modell des Akustikvorhangs für einen Einfallswinkel von 60° bei 500 Hz dargestellt. Der Energiefluss wird durch den Schalldruckgradienten um den Probenrand herum verursacht: Der Schalldruck in Bodennähe nimmt aufgrund des Beitrags des reflektierten Schalls einen größeren Wert an, während der Schalldruck vor dem Absorber aufgrund des Schallabsorptionseffekts kleiner wird. Der Energiefluss erfolgt um den Rand der Probe herum, und seine Auswirkung auf den Schallabsorptionskoeffizienten kann durch Vergrößerung der Probenfläche reduziert werden. Daher ist die Probengröße für die Messung des Absorptionskoeffizienten des Hallraums in ISO:354 geregelt.
Die Visualisierung der Amplitude und des Pfeils der Schallintensität bei 500 Hz für einen Einfallswinkel von 60°.
Fazit
In diesem Blog-Beitrag wurde der theoretische Aspekt der Schallabsorption an Rändern vorgestellt und untersucht, wie sich die Art des schallabsorbierenden Randmodells auf die Schallabsorptionsleistung auswirkt. Die Physik-Interfaces Ray Acoustics, Pressure Acoustics, Frequency Domain und Pressure Acoustics, Time Explicit in COMSOL® sind gut für die Modellierung der Raumakustik geeignet. Das Interface Ray Acoustics basiert auf geometrischer Akustik und kann das Verhalten von Schallwellen nicht genau erfassen. Unsere Implementierung kann jedoch das Verhalten der Schallabsorption auf Oberflächen in Abhängigkeit vom Einfallswinkel erfassen, was zur Verbesserung der Genauigkeit der Raumakustikmodellierung beiträgt.
Die wellenbasierten Ansätze modellieren die Schallabsorptionseigenschaften an den Rändern exakt. Die Features Poroacoustics und Interior Impedance werden verwendet, um die erweiterte Reaktivität des schallabsorbierenden Randes zu modellieren. Das Interface Pressure Acoustics, Frequency Domain kann diese Bedingungen problemlos bewältigen, da die Methode von Natur aus frequenzabhängig ist. Andererseits ist die Modellierung der Randbedingungen der erweiterten Reaktion im Zeitbereich aufgrund der Schwierigkeit, die Frequenzabhängigkeit der Absorptionseigenschaft im Zeitbereich zu modellieren, eine große Herausforderung. Wir können jedoch das Feature Poroacoustics im Zeitbereich verwenden, um poröse Absorber mit erweiterter Reaktivität zu modellieren. Die Zeitbereichsversion dieses Features verwendet eine effiziente Hilfsdifferentialgleichungsmethode, um die Frequenzabhängigkeit in porösen Materialien zu berücksichtigen. So können Sie die schallabsorbierenden Randmodelle flexibel entsprechend der Konfiguration der Absorber auswählen.
In einem zukünftigen Blog-Beitrag werden wir das Feature Poroacoustics für den Zeitbereich nutzen, um zu untersuchen, wie sich die Wahl der schallabsorbierenden Ränder auf die Akustik in einem Meetingraum auswirkt.
Referenzen
- Z. Maekawa, J. H. Rindel and P. Lord. Environmental and Architectural Acoustics. CRC Press, 2010.
- J.F. Allard and N. Atalla. Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials. Wiley, 2009.
- T. Sakuma, S, Sakamoto and T. Otsuru. Computational Simulation in Architectural and Environmental Acoustics: Methods and Applications of Wave-Based Computation. Springer, 2014.
Kommentare (0)