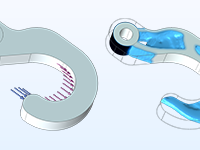
Strukturelle Topologie-Optimierung
Topologie-Optimierung eines Hakens, bei der das Material für eine optimale Beanspruchung bei einem bestimmten Gesamtgewicht verteilt wird.
Multiphysik-Modelle optimieren
Das Optimization Module, ein Add-On zu COMSOL Multiphysics®, bietet Werkzeuge zur Parameter-, Form- und Topologieoptimierung sowie zur Parameterschätzung. Zusammen mit anderen Modulen aus der COMSOL Produktpalette können Sie Geräte und Prozesse optimieren, die Phänomene wie Elektromagnetismus, Strukturmechanik, Akustik, Strömung, Wärmetransport und mehr beinhalten. In Kombination mit dem CAD Import Module, dem Design Module oder einem der LiveLink™ Produkte für CAD können Sie geometrische Abmessungen optimieren.
Ausgehend von einer zu verbessernden Zielfunktion und einer Reihe von zu ändernden Konstruktionsvariablen sowie einer optionalen Reihe von Beschränkungen sucht die Software nach einem optimalen Design. Alle Eingaben in das Modell - seien es geometrische Abmessungen, Teileformen, Materialeigenschaften oder die Materialverteilung - können als Designvariablen behandelt werden, und jede Modellausgabe kann als Zielfunktion verwendet werden, die dann minimiert oder maximiert wird.
COMSOL kontaktieren
Kombinieren Sie das Optimization Module mit einem der COMSOL® Add-On Produkte, um eine Optimierung in verschiedenen Physikbereichen durchzuführen.

Topologie-Optimierung eines Hakens, bei der das Material für eine optimale Beanspruchung bei einem bestimmten Gesamtgewicht verteilt wird.
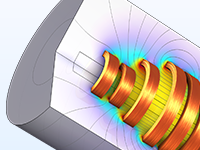
Parameter- und Formoptimierung einer Spule mit zehn Windungen, optimiert im Hinblick auf die magnetische Flussdichte und die Verlustleistung.
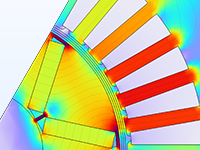
Parameteroptimierung eines Elektromotors, um die beste Position und Form der Permanentmagnete im Hinblick auf das Drehmoment zu ermitteln.
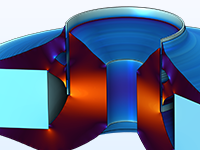
Topologie-Optimierung eines Magnetkreises, der in einem Lautsprecher-Treiber verwendet wird, um das nichtlineare Verhalten bei großen Auslenkungen zu reduzieren.

Durch die Optimierung der Form einer Hochtonkalotte und des Wellenleiters eines Lautsprechers werden eine flachere Ansprechkurve und ein verbessertes Abstrahlverhalten erzielt.
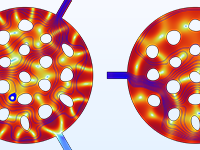
Formoptimierung eines akustischen Demultiplexers; die akustische Energie wird an unterschiedliche Ausgangsports für verschiedene Frequenzbänder geleitet.
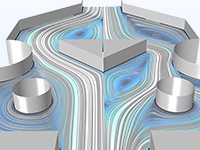
Parameter-, Form- und Topologieoptimierung für ein Tesla-Mikroventil zur Maximierung des Druckabfallverhältnisses bei wechselnder Fließrichtung
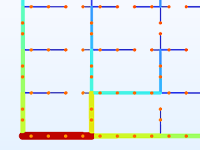
Topologie-Optimierung des Layouts eines Fernwärmenetzes.
COMSOL Multiphysics® bietet maßgeschneiderte Interfaces mit speziellen Lösern für verschiedene Arten der Optimierung.
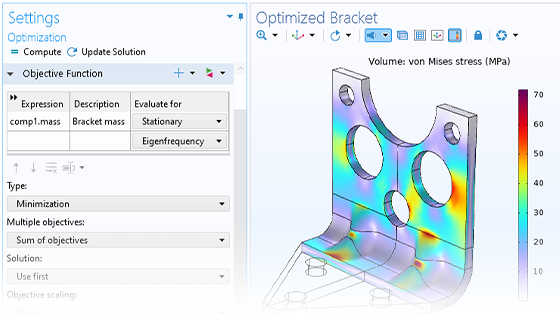
Um eine Parameteroptimierung in COMSOL Multiphysics® einzurichten, müssen Sie lediglich eine allgemeine Optimization Studie hinzufügen. Ein zugehöriges Einstellungsfenster fordert Sie auf, eine Zielfunktion, Kontrollvariablen und -parameter sowie Nebenbedingungen hinzuzufügen. Bei den Parametern, die Sie für die Parameteroptimierung verwenden, kann es sich um dieselben Parameter handeln, die auch für die Erstellung des Modells verwendet wurden, z.B. Geometriemaße, Materialeigenschaften oder Randbedingungen. Während ein parametrischer Sweep Ihnen einen Überblick über den Design-Parameterraum verschafft, erhalten Sie bei einer Parameteroptimierung die optimalen Parameter und Zielfunktionswerte.
Wenn Sie eine Parameteroptimierung mit Parametern durchführen, die Geometriemaße definieren, ist bei jeder Iteration eine erneute Vernetzung erforderlich - ein Prozess, der mit dem Optimization Module vollautomatisch abläuft. Die optimale Lösung ist immer ein echtes CAD-Teil, das sofort in branchenübliche CAD-Formate exportiert werden kann. Dazu benötigen Sie das CAD Import Module, Design Module oder eines der LiveLink™ Produkte für CAD.
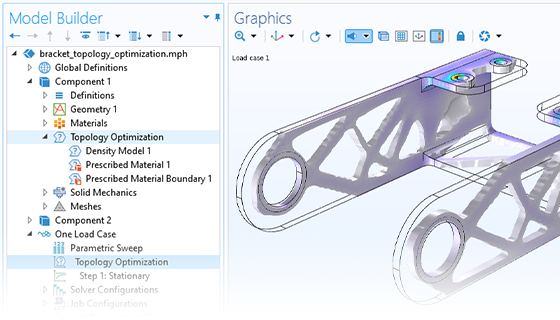
Die Topologieoptimierung bietet eine noch größere Freiheit bei der Geometrievariation als die Parameter- und Formoptimierung. Bei diesem Ansatz kann während des Optimierungsprozesses Material entfernt und hinzugefügt werden, so dass Löcher in der Geometrie entstehen können, die ursprünglich nicht im Design vorhanden waren. Diese Methode führt in der Regel zu einem organisch anmutenden Design und ist eine beliebte Methode zur Gewichtsreduzierung. Für die Topologieoptimierung stehen ein spezielles Interface und eine Studie zur Verfügung.
Genau wie bei der Formoptimierung ist auch bei der Topologieoptimierung kein Remeshing erforderlich. Das optimale und geglättete Design wird in den Dateiformaten STL, 3MF oder PLY zur weiteren Verwendung in einer anderen Software oder zur Verifikationsanalyse innerhalb von COMSOL Multiphysics® zur Verfügung gestellt.
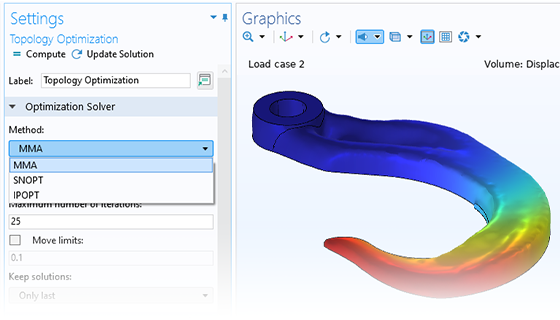
Gradientenbasierte Optimierungsmethoden werden verwendet, wenn die Ableitungen effizient mit der adjungierten Methode berechnet werden können. Dies ist für benutzerdefinierte Ziele oder Nebenbedingungen möglich, solange diese differenzierbar sind. Zu verdanken ist dies der Kerntechnologie von COMSOL Multiphysics®, die eine symbolische Differenzierung ermöglicht, die auch die nötige Flexibilität für die Lösung benutzerdefinierter Multiphysikprobleme bietet.
Die gradientenbasierte Optimierung kann mit Tausenden, ja sogar Millionen von Designvariablen verwendet werden. Dies ist häufig bei der Form- oder Topologieoptimierung der Fall, bei der die Designvariablen Feldgrößen darstellen, die im Raum verteilt sind und in jedem Netzelement durch unterschiedliche Werte repräsentiert werden.
Die gradientenbasierten Methoden berechnen simultan alle analytischen Ableitungen, während die ableitungsfreien Methoden jede Ableitung annähern müssen und mehr Zeit benötigen, wenn die Anzahl der Designvariablen steigt.
Die im Optimization Module enthaltenen gradientenbasierten Methoden sind:
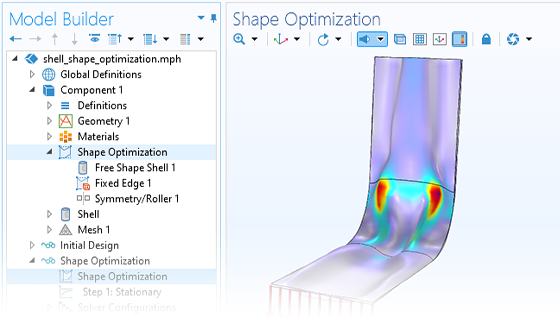
Als Alternative zum Variieren einer Reihe von CAD-Parametern können Sie die Geometrie mehr oder weniger frei verformen, indem Sie die integrierten Funktionen zur Formoptimierung verwenden. Dieser Ansatz ermöglicht eine größere Freiheit und kann manchmal sogar bessere Ergebnisse liefern als die Parameteroptimierung. Es gibt eine Reihe von speziellen Interfaces, mit denen Sie die zulässigen Verformungen von Rändern in einem 2D- oder 3D-Modell einfach definieren können. Darüber hinaus gibt es ein spezielles Feature für die Optimierung der Form von Schalenelementen sowie einen Studientyp für die Formoptimierung zur Steuerung der Löser.
Die Werkzeuge für die Formoptimierung von Festkörpern basieren auf Methoden, die das Netz auf kontrollierte Weise deformieren, ohne dass eine Neuvernetzung erforderlich ist. Die optimale Geometrie liegt dann in einem facettierten Oberflächennetzformat vor, wie STL, 3MF oder PLY. Diese Geometrie kann dann in einer separaten Analyse innerhalb von COMSOL Multiphysics® wiederverwendet oder zur Verwendung in einer anderen Software exportiert werden.
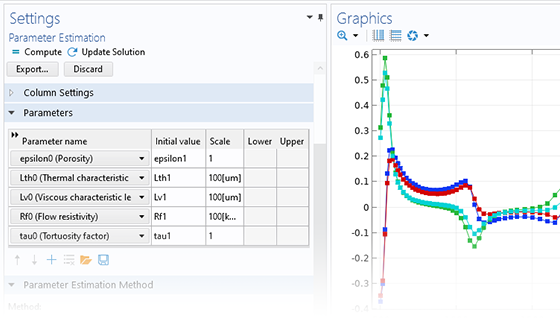
Ein Modell ist immer nur so genau wie seine Eingangsparameter, aber es kann schwierig sein, genaue Materialparameter von Zulieferern zu erhalten. Um Nichtlinearitäten zu berücksichtigen, müssen Sie möglicherweise Versuche durchführen. Es kann jedoch eine Herausforderung sein, solche Versuche zu planen, die es Ihnen ermöglichen, die gewünschten Parameter mit analytischen Methoden zu extrahieren.
Eine Lösung für diese Probleme ist die Verwendung der Parameterschätzungsfunktion des Optimization Modules, um den Parametersatz eines Modells zu finden, der die Abweichung zwischen dem physikalischen und dem simulierten Experiment minimiert. Zusätzlich zum Interface für die allgemeine Parameterschätzung steht ein spezialisiertes Interface für das Curve Fitting zur Verfügung, um eine Kurve (repräsentiert durch eine Modellgröße) an zeitabhängige Daten anzupassen.
Die Methode zur Parameterschätzung basiert auf der Anpassung nach dem Prinzip der kleinsten Quadrate und kann verwendet werden, wenn die Referenzdaten eine Funktion der Zeit oder eines einzelnen Parameters sind. In vielen Fällen erhalten Sie eine Schätzung der Varianz und des Zuverlässigkeitsgrads der geschätzten Parameter.
Für den Einstieg in die Parameterschätzung steht eine gebrauchsfertige App zur Verfügung, die die Verwendung von integrierten Übungsbeispielen oder importierten Messdaten sowie die Eingabe von benutzerdefinierten Modellausdrücken für die anzupassende Kurve ermöglicht.
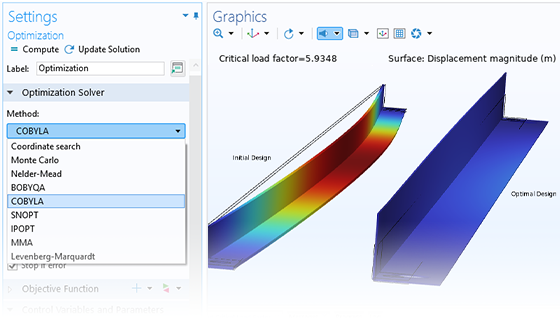
Gradientenfreie Optimierungsmethoden werden verwendet, wenn die vom Optimierungslöser benötigten Suchrichtungen nur indirekt berechnet werden können. Dies ist häufig bei der Parameteroptimierung der Fall, bei der die Kontrollvariablen Geometriedimensionen darstellen und bei jedem Iterationsschritt eine Neuvernetzung erforderlich ist.
Die im Optimization Module enthaltenen gradientenfreien Methoden sind:
Die Verwendung des Application Builder in Verbindung mit dem Optimization Module eröffnet einem größeren Kreis von Anwendern die Möglichkeit, Optimierungsstudien unabhängig durchzuführen, ohne einen Simulationsexperten zu Rate ziehen zu müssen.
Optimierungsmodelle können beispielsweise eine Parameterschätzung auf der Grundlage experimenteller Daten beinhalten; eine auf diese spezielle Aufgabe zugeschnittene App würde es einem Anwender ermöglichen, verschiedene Sätze von experimentellen Daten einzugeben, ohne sich um die Details des Optimierungsmodells selbst zu kümmern.
Die Verwendung von Apps bietet außerdem einen effizienteren Workflow für die optimale Steuerung. Das Optimization Module kann verwendet werden, um herauszufinden, welche instationäre Eingabe eine gewünschte instationäre Ausgabe ergibt. In diesem Fall möchten Sie vielleicht die gewünschte Ausgabe auf der Grundlage von experimentellen Ergebnissen anpassen. Die Erstellung einer App für diese Aufgabe bündelt die Komplexität dieses Prozesses in einem individuellen Interface, das es verschiedenen Anwendern ermöglicht, Simulationen zur optimalen Steuerung auszuführen, indem sie einfach ihre gewünschten Ergebnisse angeben.
Jedes Unternehmen und jeder Simulationsbedarf ist einzigartig.
Um zu beurteilen, ob die COMSOL Multiphysics® Software Ihren Anforderungen entspricht, kontaktieren Sie uns bitte. Wenn Sie mit einem unserer Vertriebsmitarbeiter sprechen, erhalten Sie persönliche Empfehlungen und vollständig dokumentierte Beispiele, die Ihnen helfen, das Beste aus Ihrer Evaluierung herauszuholen und die beste Lizenzoption für Ihre Bedürfnisse zu wählen.
Klicken Sie einfach auf die Schaltfläche "COMSOL kontaktieren", geben Sie Ihre Kontaktdaten und Ihre spezifischen Kommentare oder Fragen ein und senden Sie Ihre Anfrage ab. Sie erhalten innerhalb eines Werktages eine Antwort von einem Vertriebsmitarbeiter.
Fordern Sie eine Software-Demo an