Modellieren Sie Strömung in porösen Medien mit dem Subsurface Flow Module

Eine Nahansicht eines Reservoirmodells, das die Ausbreitung des Kohlendioxids zeigt.

Eine Nahansicht eines geothermischen Dublettenmodells in der Wärmekamera-Farbtabelle.

Eine Nahansicht eines multilateralenBohrlochmodells, das den Druck und die Geschwindigkeit zeigt.

Eine Nahansicht eines mikroskopischen Modells einer Porenstruktur mit blauen und magentafarbenen Stromlinien.

Die unterirdische Strömung beeinflusst viele geophysikalische Eigenschaften

Der Bedarf nach fortgeschrittener Modellierung poröser Medien erstreckt sich auf viele Branchen und Anwendungen. Das Subsurface Flow Module hilft Landwirtschafts-, Bau- und Umweltingenieuren und -wissenschaftlern in verschiedenen Industrien, unterirdische Strömungen zu analysieren und ihre Designs und Prozesse zu optimieren.

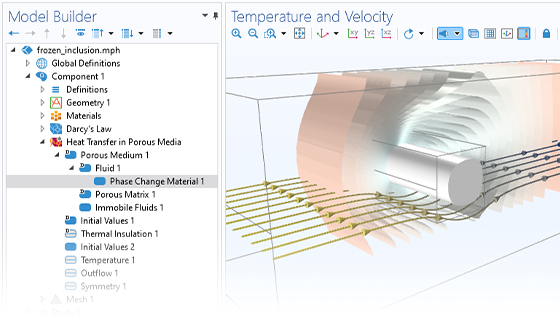
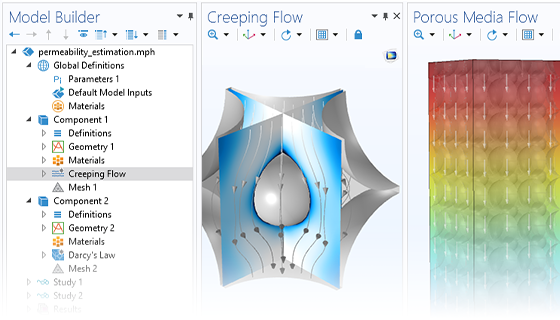
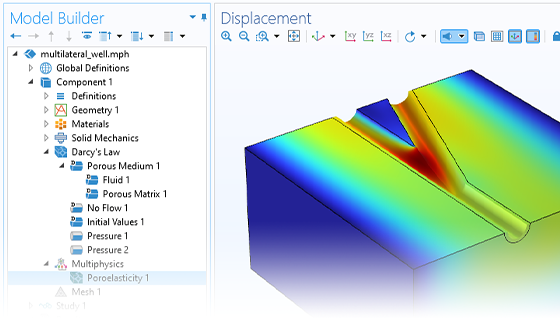
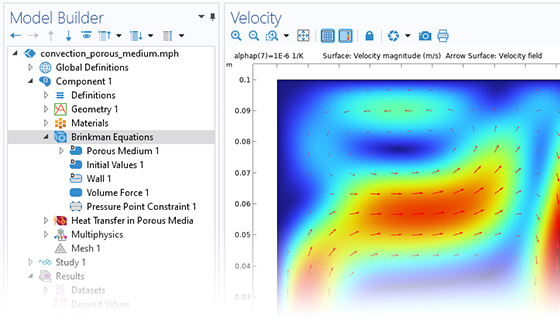
Mit COMSOL Multiphysics^® können Sie die Auswirkungen poröser Medien auf Transportprozesse für die Hydrologie, geotechnische Anwendungen, das Reservoir Engineering und die Umwelttechnik simulieren. Die Software bietet umfassende Modellierungsfunktionen, die automatisch die Gleichungen aufstellen und lösen, die spezifisch für die zu modellierende Art der unterirdischen porösen Medienströmung sind.

Flachwassergleichungen

Mit den Flachwassergleichungen können Sie eine Strömung unterhalb einer freien Oberfläche modellieren, bei der die horizontale Längenskala viel größer ist als die vertikale Längenskala. Die Gleichungen können zum Beispiel verwendet werden, um die Auswirkungen von Tsunamis und Überschwemmungen zu modellieren. Sie erhalten die Gleichungen, indem Sie die Navier-Stokes-Gleichungen über die Tiefe mitteln. Die abhängigen Variablen sind die Wassertiefe und der Impulsfluss.

Eine Nahansicht der Wasseroberfläche eines Tsunami-Auflaufmodells.

Eine Nahansicht des Aufpralls einer Wasserwelle auf eine Säule.

Features und Funktionalitäten im Subsurface Flow Module

Das Subsurface Flow Module bietet Funktionen zur Modellierung von Strömungen und anderen Phänomenen in unterirdischen Umgebungen.

Eine Nahansicht des Model Builder mit dem hervorgehobenen Knoten Porous Medium und einer 2D-Darstellung im Grafikfenster.

Langsame Strömung in porösen Medien

Das Darcy-Gesetz beschreibt die Fluidbewegung durch Zwischenräume in einem vollständig gesättigten porösen Medium, die von einem Druckgradienten angetrieben wird, wobei der Transport von Impulsen aufgrund von Scherspannungen in dem Fluid vernachlässigbar ist. Das Interface Darcy's Law berechnet den Druck, und das Geschwindigkeitsfeld wird dann durch den Druckgradienten, die Viskosität und die Permeabilität des Fluids bestimmt.

Eine Nahansicht des Model Builder mit dem hervorgehobenen Knoten Porous Matrix und einem 3D-Modell im Grafikfenster.

Variabel gesättigte Strömung in porösen Medien

Die Richards-Gleichung beschreibt den Fluidfluss durch ein teilweise gesättigtes poröses Medium und berücksichtigt dabei die Veränderungen der hydraulischen Eigenschaften, wenn das Fluid einige Poren füllt und aus anderen abfließt. Das Interface Richards' Equation enthält integrierte Modelle zur Fluidretention, aus denen Sie wählen können, z.B. das van-Genuchten- oder das Brooks-Corey-Modell. Ähnlich wie bei dem Interface Darcy's Law wird nur der Druck berechnet. Die Richards-Gleichung ist nichtlinear, da die hydraulischen Eigenschaften je nach Sättigung variieren.

Eine Nahansicht des Model Builder mit dem hervorgehobenen Knoten Phase Change Material und einem Eiseinschlussmodell im Grafikfenster.

Wärmetransport in porösen Medien

Der Wärmetransport in porösen Medien erfolgt durch Wärmeleitung, Konvektion und Dispersion. Die Dispersion wird durch den gewundenen Weg des Fluids im porösen Medium verursacht und wird durch das Einbeziehen zusätzlicher Effekte über die mittlere Konvektion hinaus beschrieben. In vielen Fällen kann die feste Phase aus mehreren Materialien mit unterschiedlichen Wärmeleitfähigkeiten bestehen, und es kann auch eine Reihe von unterschiedlichen Fluiden vorhanden sein. Das Interface Heat Transfer in Porous Media berücksichtigt diese Faktoren automatisch, und es werden Mischungsregeln zur Berechnung der effektiven Wärmetransporteigenschaften bereitgestellt.

Das Fluid im Porenraum kann auch einen oder mehrere Phasenübergänge durchlaufen, was bei der Modellierung des Prozesses des Gefrierens von Böden von Interesse ist. Eine spezielle Funktion Phase Change Material ermöglicht es Ihnen, diesen und ähnliche Prozesse zu modellieren, indem Sie zwei Materialien und die Phasenwechseleigenschaften (Phasenwechseltemperatur, Übergangsintervall und latente Wärme) angeben.

Eine Nahansicht des Model Builder mit dem hervorgehobenen Knoten Creeping Flow und Teilen eines Modells der Kriechströmung und eines Modells der Strömung in porösen Medien.

Laminare und Kriechströmung

Für maximale Flexibilität bietet das Subsurface Flow Module die Möglichkeit, sowohl die Strömung in freien als auch in porösen Medien zu simulieren. Mit den Interfaces Laminar Flow und Creeping Flow können Sie instationäre und stationäre Strömungen bei relativ niedrigen Reynolds-Zahlen modellieren. Die Viskosität eines Fluids kann von der lokalen Zusammensetzung und Temperatur oder jedem anderen Feld abhängen, das in Verbindung mit der Fluidströmung modelliert wird.

Eine Nahansicht des Model Builder mit dem hervorgehobenen Knoten Poroelasticity und dem Grafikfenster, das ein multilaterales Bohrlochmodell in der Farbtabelle Rainbow zeigt.

Poroelastizität

Verdichtung und Quellung können mit einem speziellen physikalischen Interface für Poroelastizität modelliert werden, das eine instationäre Formulierung des Darcy-Gesetzes mit einem linear elastischen Materialmodell der porösen Matrix kombiniert. Die Fluidströmung wirkt sich auf die Kompressibilität des porösen Mediums aus, und Änderungen der volumetrischen Dehnungen wirken sich wiederum auf den Stofftransport aus. Um diese Effekte zu ermöglichen, enthält das Multiphysik-Interface Poroelasticity einen Ausdruck des Spannungstensors als Funktion der volumetrischen Dehnung und des Biot-Willis-Koeffizienten.

Eine Nahansicht des Model Builder mit dem ausgewählten Interface Brinkman Equations und einem Modell eines porösen Mediums, das in der Farbtabelle Rainbow im Grafikfenster angezeigt wird.

Schnelle Strömung in porösen Medien

Die Brinkman-Gleichungen berücksichtigen schnell fließende Fluide in porösen Medien, wobei das kinetische Potential aus Fluidgeschwindigkeit, Druck und Schwerkraft die Strömung antreibt. Das Interface Brinkman Equations verallgemeinert das Gesetz von Darcy, um die Dissipation der kinetischen Energie durch viskose Scherung zu berechnen, ähnlich wie bei den Navier-Stokes-Gleichungen. Zusätzlich können Sie mit dem CFD Module schnelle Strömungen in porösen Medien mit turbulenten Strömungen kombinieren.

Eine Nahansicht der Einstellungen für Porous Matrix und zwei 2D-Plots im Grafikfenster

Nicht-Darcysche Strömung

Das Darcy-Gesetz und die Brinkman-Korrektur des Darcy-Gesetzes gelten nur, wenn die Zwischenraumgeschwindigkeit in den Poren so niedrig ist, dass die Annäherung an die Kriechströmung gilt. Für höhere Zwischenraumgeschwindigkeiten kann eine zusätzliche nichtlineare Korrektur in die Impulsgleichung aufgenommen werden. Im Subsurface Flow Module stehen mehrere Permeabilitätsmodelle für die Modellierung von nicht-Darcyschen Strömungen in porösen Medien zur Verfügung: Das Interface Brinkman Equations enthält die Modelle Forchheimer und Ergun, und die Interfaces Darcy's Law und Multiphase Flow in Porous Media enthalten die Modelle Forchheimer, Ergun, Burke-Plummer und Klinkenberg.

Eine Nahansicht des Model Builders mit dem hervorgehobenen Knoten Fluid and Fracture Properties und zwei Grafikfenstern mit einem geklüfteten Reservoirmodell.

Strömung in Spalten

Spalten innerhalb eines porösen Mediums beeinflussen die Strömungseigenschaften durch die poröse Matrix. Das Interface Fracture Flow löst den Druck an internen (2D-) Rändern innerhalb einer 3D-Matrix, basierend auf einer benutzerdefinierten Öffnung. Der berechnete Druck wird automatisch mit der Physik gekoppelt, die die poröse Medienströmung in der umgebenden Matrix beschreibt – eine Annäherung, die Zeit und Rechenressourcen bei der Vernetzung der Spalten spart.

Eine Nahansicht der Einstellungen für Mehrphasenströmung in porösen Medien, wobei der Abschnitt Coupled Interfaces ausgeklappt ist und ein Linsenmodell im Grafikfenster angezeigt wird.

Mehrphasige Strömung in porösen Medien

Die Funktionalität für den Phasentransport kann mit dem Interface Darcy's Law kombiniert werden, um die Mehrphasenströmung in porösen Medien mit einer beliebigen Anzahl von Phasen zu simulieren. Nutzer können Eigenschaften poröser Medien wie relative Permeabilitäten und Kapillardrücke zwischen den Phasen angeben. Diese Eigenschaften werden zwischen den Phasen mit einer Multiphysik-Kopplung weitergegeben, die das Interface Phase Transport in Porous Media mit dem Interface Darcy's Law verbindet.

Eine Nahansicht des Model Builders mit dem hervorgehobenen Knoten Fluid und einem Lösungsmitteltransportmodell im Grafikfenster.

Transport chemischer Spezies in porösen Medien und Spalten

Die COMSOL Multiphysics^® Simulationssoftware bietet intuitiv zu bedienende Funktionen zur Definition des Stofftransports in verdünnten Lösungen oder Mischungen einer beliebigen Anzahl chemischer Spezies durch Konvektion, Diffusion, Dispersion, Adsorption und Verflüchtigung. Diese Funktionen lassen sich leicht mit Definitionen von reversiblen, irreversiblen und Gleichgewichtsreaktionskinetiken verbinden, indem Sie das Subsurface Flow Module mit dem Chemical Reaction Engineering Module kombinieren. Mit dem Subsurface Flow Module kann diese Funktionalität auf poröse Medien und Spalten erweitert werden.

Subsurface Flow Module

Die unterirdische Strömung beeinflusst viele geophysikalische Eigenschaften

Flachwassergleichungen